吉林省五盟校 高二数学上学期期中联考试卷 理(PDF，无答案)试卷VIP免费

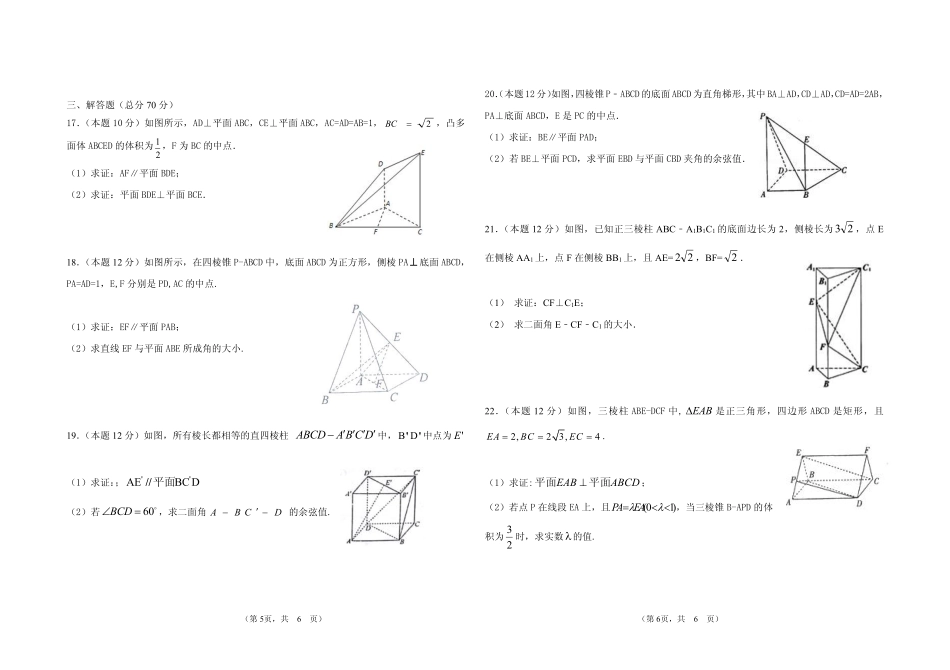
（第1页，共6页）（第2页，共6页）2018—2019学年度上学期五盟校期中考试高二理数试题出题人：宋文峰一、选择题:本题共12小题，每题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。1．设m、n是不同的直线，,是不同的平面，有以下四个命题：①若//,m，则m；②若//,,mm则；③若//,,nnmm则；④若//,,则nn.其中，真命题的个数为（）A．1B．2C．3D．42．下面的图形可以构成正方体的是（）A.B.C.D.3．在空间直角坐标中，点B是A（1，2，3）在yOz坐标平面内的射影，O为坐标原点，则|OB|等于（）A．14B．13C．32D．114．已知一个几何体的三视图如图所示，则该几何体的体积为A．4B．6C．8D．165．正方体ABCD-A1B1C1D1中，M、N分别为棱AB，DD1中点，则异面直线A1M与C1N所成的角是（）A．0B．4C．3D．26．正方体的内切球，与各棱相切的球，外接球的体积之比为（）A．1：2：3B．23:21:1C．33:22:1D．3:2:17．某一简单几何体的三视图如图所示,则该几何体的外接球的表面积是（）.A．13B．16C．25D．278．如图所示是水平放置三角形的直观图，点D是△ABC的BC边中点，AB，BC分别与y′轴、x′轴平行，则三条线段AB，AD，AC中()A．最长的是AB，最短的是ACB．最长的是AC，最短的是ABC．最长的是AB，最短的是ADD．最长的是AC，最短的是AD（第3页，共6页）（第4页，共6页）9．如图，二面角l的大小为，A，B为棱l上相异的两点，射线AC,BD分别在这个二面角的两个半平面内，且都垂直于棱l．若线段AC,AB和BD的长分别为m,d和n，则CD的长为（）A．2222cosmndmnB．2222cosmndmnC．2222sinmndmnD．2222sinmndmn10．如图是一个几何体的三视图，根据图中的数据（单位：cm），可知此几何体的体积是（）A．24cm3B．3643cmC．362522cmD．3248582cm11．《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的表面积为（）A．14B．642C．862D．84212．如图，四棱锥P-ABCD中，PAB为正三角形，四边形ABCD为正方形且边长为2，平面PAB平面ABCD，四棱锥P-ABCD的五个顶点都在一个球面上，则这个球的表面积是（）A．272128B．37C．28D．328第II卷（非选择题）二、填空题:每题5分共20分13．已知23a，4b，bam，nmbaban,,,135则_____.14．已知m、n是两条不重合的直线，、是两个不重合的平面，有下列命题：①若nmn//,，则//,//mm；②若mm,，则//；③若nmm,//，则n；④若nm,，则nm其中所有真命题的序号是．15．如图所示，在正三棱锥S-ABC中，M、N分别是SC、BC的中点，且MN⊥AM，若侧棱SA＝23，则正三棱锥SABC外接球的表面积是________．16．棱长为1的正方体ABCD-A1B1C1D1中，点P1,P2分别是线段AB，BD1（不包括端点）上的动点，且线段P1P2平行平面A1ADD1，则四面体P1P2AB1的体积的最大值是（第5页，共6页）（第6页，共6页）三、解答题（总分70分）17．（本题10分）如图所示，AD⊥平面ABC，CE⊥平面ABC，AC=AD=AB=1，2BC，凸多面体ABCED的体积为21，F为BC的中点．（1）求证：AF∥平面BDE；（2）求证：平面BDE⊥平面BCE．18．（本题12分）如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，侧棱PA底面ABCD，PA=AD=1，E,F分别是PD,AC的中点.（1）求证：EF∥平面PAB；（2）求直线EF与平面ABE所成角的大小.19．（本题12分）如图，所有棱长都相等的直四棱柱ABCDABCD中，''DB中点为'E（1）求证：；DBCAE''//平面（2）若60BCD，求二面角ABCD的余弦值.20．（本题12分）如图，四棱锥P﹣ABCD的底面ABCD为直角梯形，其中BA⊥AD，CD⊥AD，CD=AD=2AB，PA⊥底面ABCD，E是PC的中点．（1）求证：BE∥平面PAD；（2）若BE⊥平面PCD，求平面EBD与平面CBD夹角的余弦值．21．（本题12分）如图，已知正三棱柱ABC﹣A1B1C1的底面边长为2，侧棱长为23，点E在侧棱AA1上，点F在侧棱BB1上，且AE=22，BF=2．（1）求证：CF⊥C1E；（2）求二面角E﹣CF﹣C1的大小．22．（本题12分）如图，三棱柱ABE-DCF中,EAB是正三角形，四边形ABCD是矩形，且2,23,4EABCEC.（1）求证:ABCDEAB平面平面；（2）若点P在线段EA上，且(01)PAEA，当三棱锥B-APD的体积为23时，求实数的值.