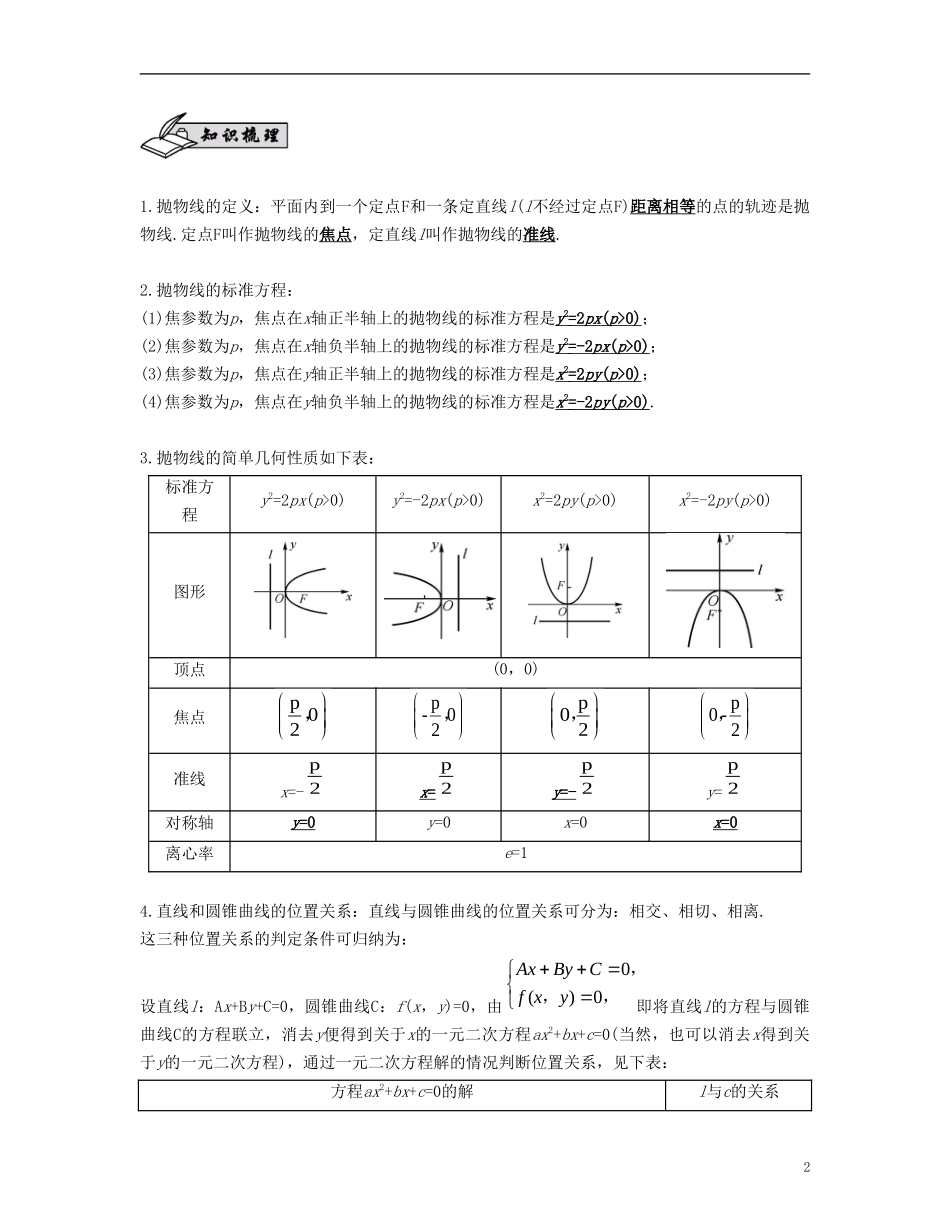
第63课抛物线(本课时对应学生用书第页)自主学习回归教材1.(选修1-1P48例2改编)顶点在原点、对称轴是坐标轴且过点(-1,2)的抛物线的方程是.【答案】y2=-4x或x2=12y【解析】设所求抛物线方程为y2=-2px或x2=2py(p>0),因为抛物线过点(-1,2),所以4=2p或1=4p,解得p=2或p=14,故所求抛物线的方程为y2=-4x或x2=12y.2.(选修1-1P50习题5改编)顶点在原点、对称轴为坐标轴、焦点在直线2x-y+4=0上的抛物线的标准方程为.【答案】x2=16y或y2=-8x【解析】由焦点在直线2x-y+4=0上,令x=0,得y=4;令y=0,得x=-2,所以焦点坐标为(0,4)或(-2,0),所以所求抛物线的方程为x2=16y或y2=-8x.3.(选修1-1P50练习2改编)若P(x0,4)是抛物线y2=-32x上一点,F是抛物线的焦点,则PF=.【答案】172【解析】抛物线y2=-32x的准线方程为x=8,又点P(x0,4)在抛物线上,所以16=-32x0,解得x0=-12,所以PF=12+8=172.4.(选修1-1P50练习4改编)在平面直角坐标系xOy中,抛物线x2=2py(p>0)上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为.【答案】4【解析】根据抛物线定义可知,该点到准线的距离也为3,从而由1+2p=3得p=4,故焦点到准线的距离为4.11.抛物线的定义:平面内到一个定点F和一条定直线l(l不经过定点F)距离相等的点的轨迹是抛物线.定点F叫作抛物线的焦点,定直线l叫作抛物线的准线.2.抛物线的标准方程:(1)焦参数为p,焦点在x轴正半轴上的抛物线的标准方程是y2=2px(p>0);(2)焦参数为p,焦点在x轴负半轴上的抛物线的标准方程是y2=-2px(p>0);(3)焦参数为p,焦点在y轴正半轴上的抛物线的标准方程是x2=2py(p>0);(4)焦参数为p,焦点在y轴负半轴上的抛物线的标准方程是x2=-2py(p>0).3.抛物线的简单几何性质如下表:标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形顶点(0,0)焦点p02,p-02,p02,p0-2,准线x=-p2x=p2y=-p2y=p2对称轴y=0y=0x=0x=0离心率e=14.直线和圆锥曲线的位置关系:直线与圆锥曲线的位置关系可分为:相交、相切、相离.这三种位置关系的判定条件可归纳为:设直线l:Ax+By+C=0,圆锥曲线C:f(x,y)=0,由0()0AxByCfxy,,,即将直线l的方程与圆锥曲线C的方程联立,消去y便得到关于x的一元二次方程ax2+bx+c=0(当然,也可以消去x得到关于y的一元二次方程),通过一元二次方程解的情况判断位置关系,见下表:方程ax2+bx+c=0的解l与c的关系2a=0b=0无解(含l是双曲线的渐进线)无公共点b≠0有一解(含l与抛物线的对称轴或与双曲线的渐近线平行)一个交点a≠0Δ>0两个不等的解两个交点Δ=0两个相等的解一个交点Δ<0无实数解无交点【要点导学】要点导学各个击破求抛物线的标准方程例1已知某抛物线的顶点在原点,对称轴为坐标轴,且过点(-3,2),求抛物线的方程并求其准线方程.【思维引导】从方程形式看,求抛物线的标准方程仅需确定一个待定系数p;从实际分析,一般需确定p和确定开口方向两个条件,否则,应展开相应的讨论.【解答】设所求的抛物线方程为y2=-2px或x2=2py(p>0),因为抛物线过点(-3,2),所以4=-2p×(-3)或9=2p·2,所以p=23或94.所以所求的抛物线的方程为y2=-43x或x2=92y,其准线方程分别为x=13和y=-98.【精要点评】确定抛物线方程的关键是要确定焦点位置与开口方向,解题时要考虑全面,注意对两种开口方向的讨论.变式1(2015·陕西卷改编)若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,则抛物线的方程为.【答案】y2=42x3【解析】抛物线y2=2px(p>0)的准线方程是x=-2p,双曲线x2-y2=1的一个焦点F1(-2,0).因为抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,所以-2p=-2,解得p=22.所以抛物线方程为y2=42x.变式2过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B两点,若线段AB的长为8,则抛物线的方程为.【答案】y2=4x【解析】由题意可知过焦点的直线方程为y=x-2p,由22-2ypxpyx,x2-3px+24p=0,所以AB=22(-1)1·22(3)-44pp=8p=2.所以抛物线方程为y2=4x.抛物线的几何性质例2(2015·南京、盐城、徐州二模)在平面直角坐标系xOy中,已知抛物线C:x2=4y的...