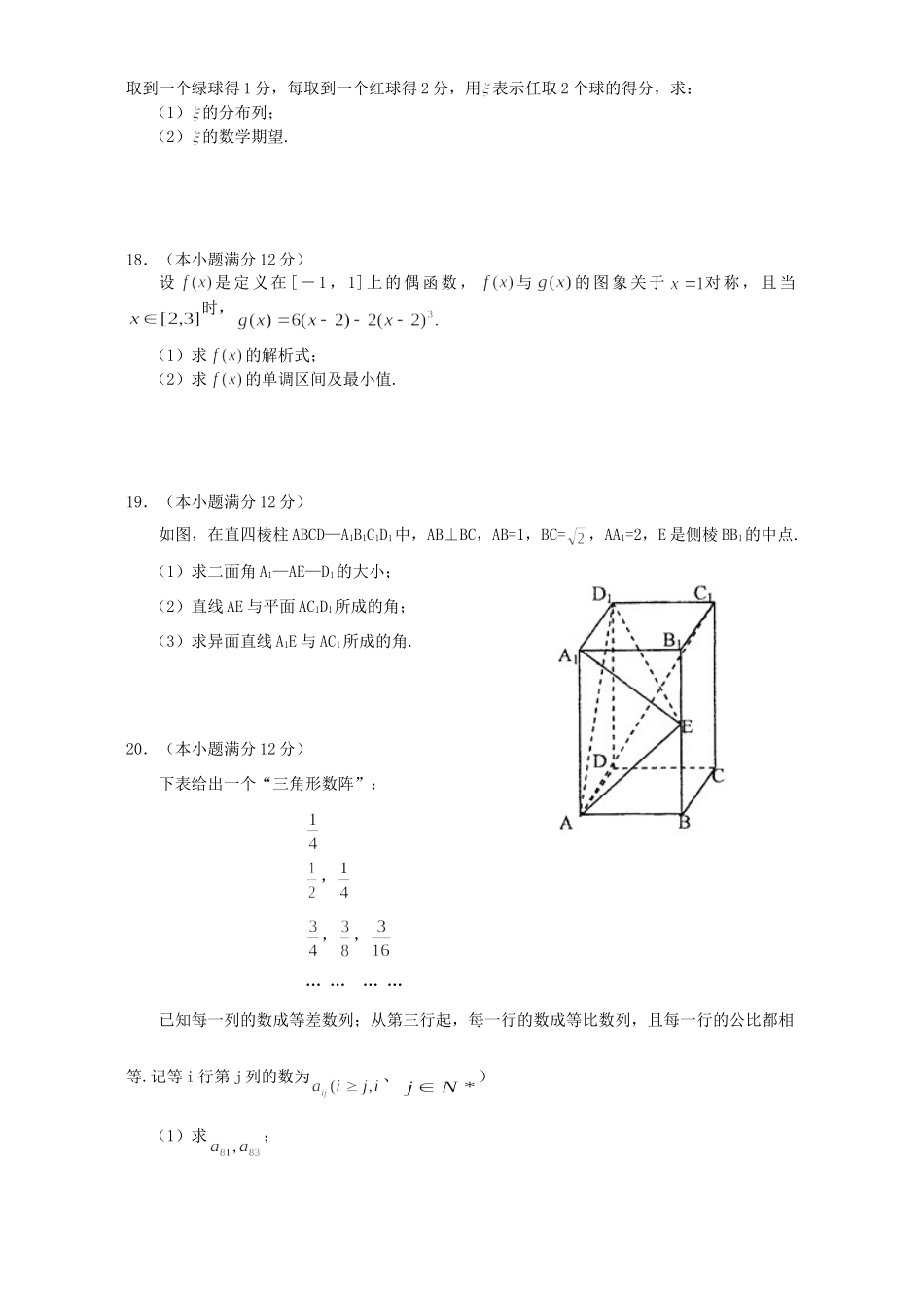
吉林省东北师大附中2005-2006学年度高三数学理科第三次月考试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两分部.共150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合,则集合=()A.{-1,0,1}B.{0,1}C.{0}D.2.不等式的解集为()A.(0,1)B.(0,+∞)C.(1,+∞)D.3.一物体的运动方程为,其中的单位是米,的单位是秒,那么物体在3秒末的瞬时速度为()A.3米/秒B.5米/秒C.7米/秒D.9米/秒4.在的展开式中含项的系数是首项为-2,公差为3的等差数列的()A.第19项B.第20项C.第21项D.第22项5.已知则等于()A.9B.-9C.9-iD.9+i6.如图,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P,P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为()A.B.C.D.7.定义R在上的奇函数上是增函数,且则满足的的取值范围是()A.(-1,0)∪(1,2)B.(-1,0)∪(1,+∞)C.(-∞,-1)∪(1,2)D.(-1,0)∪(0,1)8.过抛物线的焦点的直线交抛物线于A、B两点,O为坐标原点,则的值是()A.3B.-3C.12D.-129.在6张卡片上分别写上数字0,1,2,3,4,5,然后把它们混合,再任意排成一行,组成6位数,则得到能被5整除的6位数的概率为()A.0.2B.0.3C.0.36D.0.4610.已知双曲线的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离,则双曲线的离心率为()A.2B.3C.D.11.如图,三棱柱A1B1C1—ABC的所有棱长均为a,且侧面A1B1BA⊥底面A1B1C1,则直线C1B与平面A1B1BA所成的角的范围是()A.B.C.D.12.设是方程的两个不等的实数根,那么过点A()和B的直线与圆的位置关系是()A.相离B.相切C.相交D.不能确定第Ⅱ卷(非选择题,共90分)二、填空题:本大题共四小题,每小题4分,共16分,把答案填在题中横线上.13.为使函数在处连续,则定义.14.实数,则的最大值为.15.若对于任意的,函数的值恒为正,则的取值范围是.16.对个向量、、……,若存在个不为零的实数、、……、使++……+=0成立,则称向量、、……、线性相关.按此规定,能说明,线性相关的实数,,依次可取(写出一组即可).三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)袋中有4个黄球,3个绿球,2个红球,从中任取2个球.已知每取到一个黄球得0分,每取到一个绿球得1分,每取到一个红球得2分,用表示任取2个球的得分,求:(1)的分布列;(2)的数学期望.18.(本小题满分12分)设是定义在[-1,1]上的偶函数,与的图象关于对称,且当时,(1)求的解析式;(2)求的单调区间及最小值.19.(本小题满分12分)如图,在直四棱柱ABCD—A1B1C1D1中,AB⊥BC,AB=1,BC=,AA1=2,E是侧棱BB1的中点.(1)求二面角A1—AE—D1的大小;(2)直线AE与平面AC1D1所成的角;(3)求异面直线A1E与AC1所成的角.20.(本小题满分12分)下表给出一个“三角形数阵”:,,,…………已知每一列的数成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比都相等.记等i行第j列的数为、)(1)求;(2)写出关于i,j的表达式;(3)求21.(本小题满分12分)已知向量且.(1)求点Q的轨迹C的方程;(2)设曲线C与直线相交于不同的两点M、N,又点A(0,-1),当时,求实数的取值范围.22.(本小题满分14分)已知函数对任意的、,都有且(1)若,试求的表达式;(2)若对于,且时,不等式恒成立,求实数的取值范围.参考答案一、选择题CACBADABCABC二、填空题13.14.15.16.-2,1,1三、解答题:17.解:(1)由题意知可取的值是0,1,2,3,4其概率分布如下表:01234P(2)…………………………12分18.解:(1)当且上任意的点P(关于直线的对称点都在图象上.又是偶函数时,,…………………………6分(2)单调递减区间为[-1,0],单调递增区间为;最小值为…………12分19.解:(1)⊥面ABB1A1,∴D1A1⊥AE.又 AE=A1E=∴AE⊥面A1ED1,∴D1E⊥AE,∴∠A1ED1即为二面角A1...