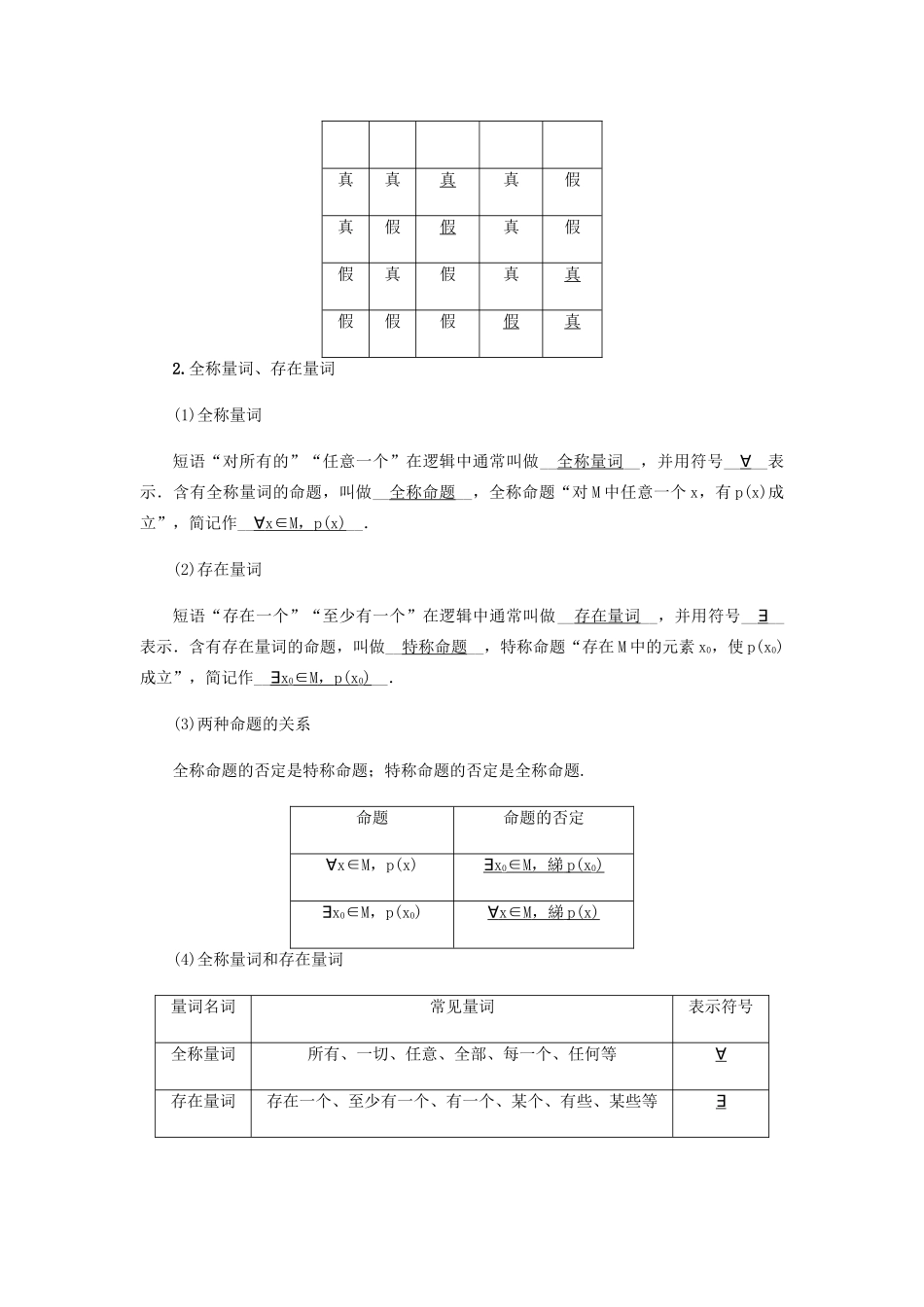
第3讲简单的逻辑联结词、全称量词与存在量词夯实基础【p6】【学习目标】1.了解逻辑联结词“或”“且”“非”的含义;2.理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定.【基础检测】1.若命题p:x=2且y=3,则綈p为________.【解析】p且q的否定为綈p或綈q,所以“x=2且y=3”的否定为“x≠2或y≠3”.【答案】x≠2或y≠32.如果命题p∨q为真命题,p∧q为假命题,那么()A.命题p,q均为真命题B.命题p,q均为假命题C.命题p,q有且只有一个为真命题D.命题p为真命题,q为假命题【解析】由p∨q为真命题,p∧q为假命题知,p,q一真一假;即p,q中只有一个真命题.【答案】C3.命题“∀x∈R,∃n0∈N*,使得n0≥x2”的否定形式是()A.∀x∈R,∃n0∈N*,使得n00,x0+a-1=0,若p为假命题,则a的取值范围是()A.(-∞,1)B.(-∞,1]C.(1,+∞)D.[1,+∞)【解析】p为假命题,等价于方程x+a-1=0无正实根,即x=1-a≤0,得a≥1.【答案】D5.命题p:∀x∈R,sinx+cosx≥-,命题q:∃x<0,e-x<1,下列选项中是真命题的是()A.p∧qB.(綈p)∨qC.p∧(綈q)D.(綈p)∧(綈q)【解析】因为命题p:sinx+cosx=sin≥-恒成立,故命题p为真命题;对于命题q:当x<0时,-x>0,从而得到e-x>1,故命题q是假命题,根据复合命题真值表可知p∧(綈q)是真命题.【答案】C【知识要点】1.逻辑联结词命题中的__“或”“且”“非”__叫逻辑联结词.(1)当p,q都是真命题时,p∧q是真命题;当p,q两个命题中至少有一个是假命题时,p∧q是假命题.(2)命题p∧q,p∨q,綈p的真假判断pqp∧qp∨q綈p真真真真假真假假真假假真假真真假假假假真2.全称量词、存在量词(1)全称量词短语“对所有的”“任意一个”在逻辑中通常叫做__全称量词__,并用符号__∀__表示.含有全称量词的命题,叫做__全称命题__,全称命题“对M中任意一个x,有p(x)成立”,简记作__∀x∈M,p(x)__.(2)存在量词短语“存在一个”“至少有一个”在逻辑中通常叫做__存在量词__,并用符号__∃__表示.含有存在量词的命题,叫做__特称命题__,特称命题“存在M中的元素x0,使p(x0)成立”,简记作__∃x0∈M,p(x0)__.(3)两种命题的关系全称命题的否定是特称命题;特称命题的否定是全称命题.命题命题的否定∀x∈M,p(x)∃x0∈M,綈p(x0)∃x0∈M,p(x0)∀x∈M,綈p(x)(4)全称量词和存在量词量词名词常见量词表示符号全称量词所有、一切、任意、全部、每一个、任何等∀存在量词存在一个、至少有一个、有一个、某个、有些、某些等∃典例剖析【p6】考点1含逻辑联结词命题的真假判断(1)若命题“p∨q”与命题“綈p”都是真命题,则()A.命题p与命题q都是真命题B.命题p与命题q都是假命题C.命题p是真命题,命题q是假命题D.命题p是假命题,命题q是真命题【解析】因为綈p为真命题,所以p为假命题,又p∨q为真命题,所以q为真命题.【答案】D(2)设命题p:∃x0∈R,x-x0+1<0;命题q:若a2>b2,则a>b,则下列命题为真命题的是()A.p∧qB.p∧(綈q)C.(綈p)∧qD.(綈p)∧(綈q)【解析】因为x2-x+1=+≥>0成立,所以不存在x0∈R,x-x0+1<0,故命题p为假命题,綈p为真命题;当a=-2,b=1时,a2>b2成立,但a>b不成立,故命题q为假命题,綈q为真命题;故命题p∧q,(綈p)∧q,p∧(綈q)均为假命题,命题(綈p)∧(綈q)为真命题.【答案】D【点评】判断含有逻辑联结词命题真假的2个步骤:(1)先判断简单命题p,q的真假;(2)再根据真值表判断含有逻辑联结词的命题的真假.考点2全称命题与特称命题(1)命题“对任意x∈R,都存在m0>1,使得m0x>ex成立”的否定为()A.对任意x∈R,都存在m0>1,使得m0x≤ex成立B.对任意x∈R,不存在m0>1,使得m0x>ex成立C.存在x0∈R,对任意m>1,都有mx0≤ex0D.存在x0∈R,对任意m>1,都有mx0>ex0【解析】 全称命题的否定是特称命题,∴命题“对任意x∈R,都存在m0>1,使得m0x>ex成立”的否定是:“...