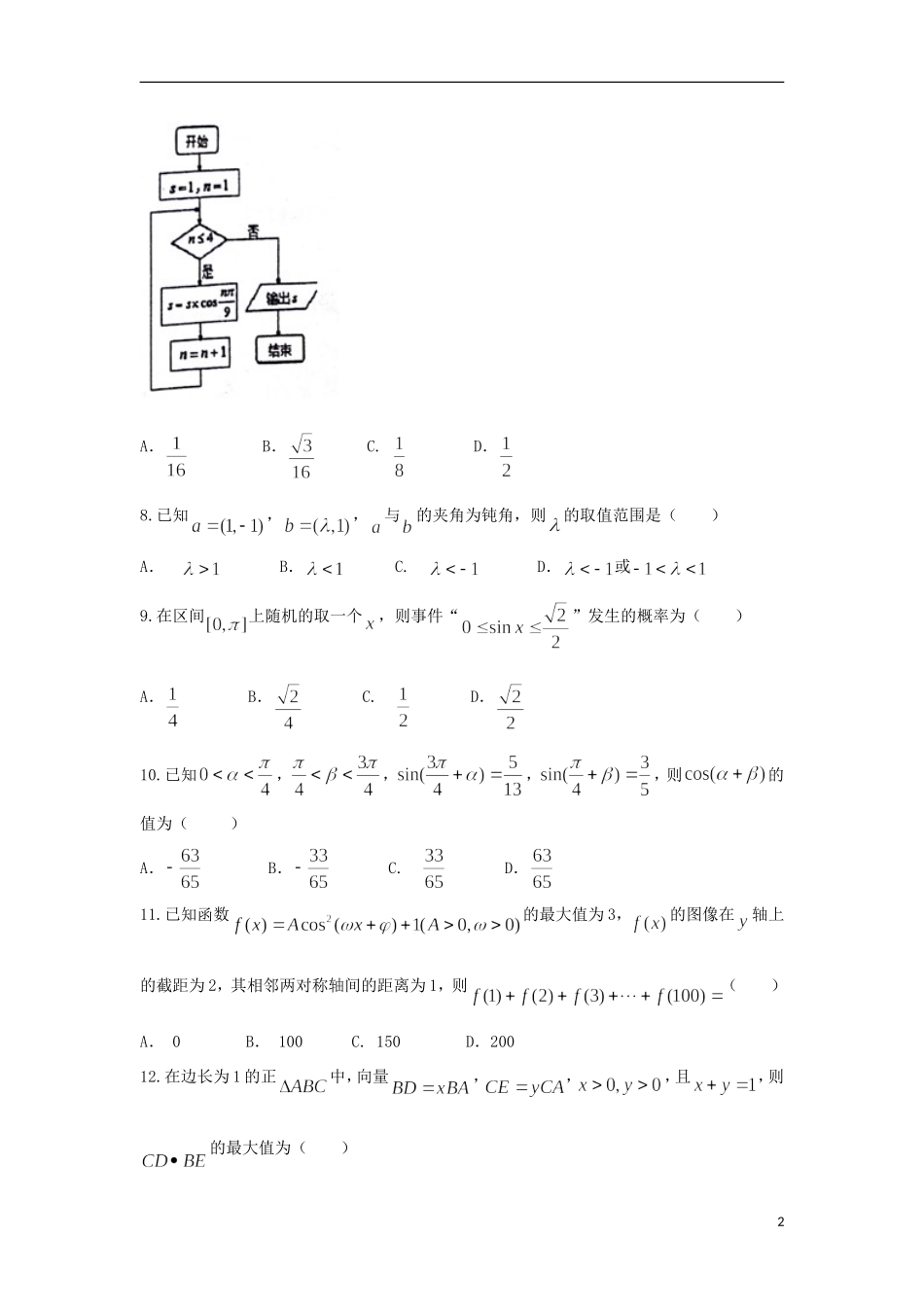
2019届高二上学期开学初考试试题数学(理)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.的值是()A.B.C.D.2.已知变量与正相关,且由观测数据算得样本平均数,,则由该观测的数据算得的线性回归方程可能是()A.B.C.D.3.下列四个函数中,以为最小正周期,且在区间上为减函数的是()A.B.C.D.4.在中,若,则是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形5.从编号为0,1,2,…,79的80件产品中,采用系统抽样的方法抽取容量为5的一个样本,若编号为42的产品在样本中,则该样本中产品的最小编号为()A.2B.10C.12D.226.在中,,,,则解的情况()A.无解B.有一解C.有两解D.不能确定7.阅读如图所示的程序框图,输出结果的值为()1A.B.C.D.8.已知,,与的夹角为钝角,则的取值范围是()A.B.C.D.或9.在区间上随机的取一个,则事件“”发生的概率为()A.B.C.D.10.已知,,,,则的值为()A.B.C.D.11.已知函数的最大值为3,的图像在轴上的截距为2,其相邻两对称轴间的距离为1,则()A.0B.100C.150D.20012.在边长为1的正中,向量,,,且,则的最大值为()2A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量的夹角为,,,则.14.函数的最大值是.15.已知不等式对一切恒成立,则实数的取值范围是.16.在中,已知,,边的中线,那么.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在平面直角坐标系中,已知向量,,.(1)若,求的值;(2)若与的夹角为,求的值.18.已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点.(1)求圆的方程;(2)当时,求直线的方程.19.的内角所对的边分别为,已知.(1)求角的大小;(2)若,求的最大值.20.某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组,,…,后得到如下部分频率分布直方图,观察图中的信3息,回答下列问题:(1)补全频率分布直方图;(2)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);(3)用分层抽样的方法在分数段为的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段内的概率.21.设函数,其中,已知.(1)求;(2)将函数的图像上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移个单位,得到函数的图像,求在上的最小值.22.已知函数,.(1)若对任意的,均有,求的取值范围;(2)若对任意的,均有,求的取值范围.4试卷答案一、选择题1-5:CBADB6-10:AADCB11、12:DC二、填空题13.14.115.16.9三、解答题17.(1)若,则,即,,即,综上所述,.(2) ,,∴若与的夹角为,则,即,则, ,5∴,则,即,综上所述,的值为.18.试题解析:(1)由题意知到直线的距离为圆半径圆的方程为[(2)设线段的中点为,连结,则由垂径定理可知,且,在中由勾股定理易知当动直线的斜率不存在时,直线的方程为时,显然满足题意;当动直线的斜率存在时,设动直线的方程为:由到动直线的距离为1得或为所求方程.19.解(1)由已知及正弦定理,得. ,∴.化简,得. ,∴. ,∴.(2)由已知及正弦定理,得.即.从而,因为,所以,化简得,6因为,可得,于是,当时,的最大值为.-20.解:(1)分数在[120,130)内的频率,因此补充的长方形的高为0.03(2)估计平均分为(3)由题意,[110,120)分数段的人数与[120,130)分数段的人数之比为1:2,用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,需在[110,120)分数段内抽取2人成绩,分别记为m,n;在[120,130)分数段内抽取4人成绩,分别记为a,b,c,d;设“从6个样本中任取2人成绩,至多有1人成绩在分数段[120,130)内”为事件A,则基本事件共有{(m,n),(m,a),(m,b),(m,c),(m,d),(n,a),(n,b),(n,c),(n,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)},共15个.事件A包含的基本事...