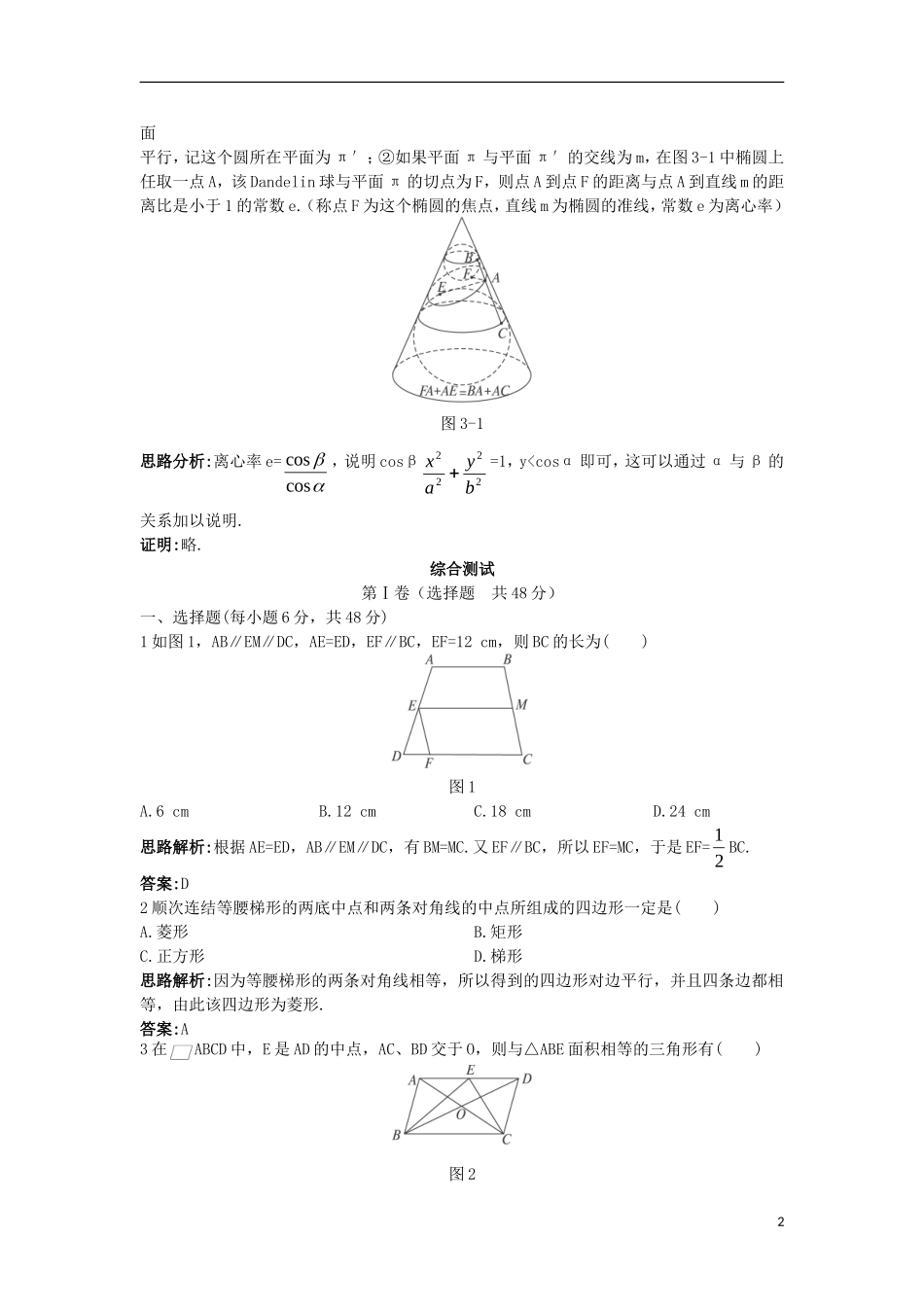
第三讲圆锥曲线性质的探讨本讲知识结构本讲测试1一条直线在平面上的正射影是__________.思路解析:要根据直线与平面的不同位置关系作出回答.当直线和平面垂直的时候,直线在平面内的射影是一个点,当直线和平面平行的时候,直线在平面内的射影是和该直线平行的一条直线.答案:一个点或和该直线平行的一条直线2已知椭圆162522yx=1上一点P到一个焦点的距离为3,那么点P到另一个焦点的距离为()A.2B.3C.5D.7思路解析:椭圆上的点到两个焦点的距离之和为常数,就是长轴的两倍.答案:D3一动圆与已知圆O1:(x+3)2+y2=1外切,圆O2:(x-3)2+y2=81内切,试求动圆圆心的轨迹方程.思路分析:两圆相切时,圆心之间的距离与两圆的半径有关,可以找到动圆圆心满足的条件.解:两定圆的圆心和半径分别为O1(-3,0),r1=1;O2(3,0),r2=9.设动圆圆心为M(x,y),半径为R,则由题设条件可得|MO1|=1+R,|MO2|=9-R.∴|MO1|+|MO2|=10,由椭圆的定义知道M在以O1、O2为焦点的椭圆上,且a=5,c=3.∴b2=a2-c2=25-9=16.故动圆圆心的轨迹方程为162522yx=1.4我们已经知道方程2222byax=1(a>b>0)表示长轴在x轴上的椭圆,试根据方程的特征,探求椭圆的一些几何性质.思路分析:从方程本身的特点入手,如将x换成-x,方程不变,说明椭圆关于y轴对称.解:x轴、y轴是椭圆的对称轴,原点是椭圆的对称中心即椭圆中心.椭圆有四个顶点A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b).还可以有别的答案.5在空间中,取直线l为轴,直线l′与l相交于O点,其夹角为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行,记β=0),则当β>α时,平面π与圆锥的交线为椭圆.试利用Dandelin双球(这两个球位于圆锥的内部,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切)证明上述结论.思路分析:按椭圆的定义证明,即平面上到两点的距离之和为定值的点的轨迹是椭圆.证明:略.6试证明以下结果:①如图3-1,一个Dandelin球与圆锥面的交线为一个圆,并与圆锥的底1面平行,记这个圆所在平面为π′;②如果平面π与平面π′的交线为m,在图3-1中椭圆上任取一点A,该Dandelin球与平面π的切点为F,则点A到点F的距离与点A到直线m的距离比是小于1的常数e.(称点F为这个椭圆的焦点,直线m为椭圆的准线,常数e为离心率)图3-1思路分析:离心率e=coscos,说明cosβ2222byax=1,y