工程力学-课后习题答案-第四版-北京师范大学-东北大学VIP免费

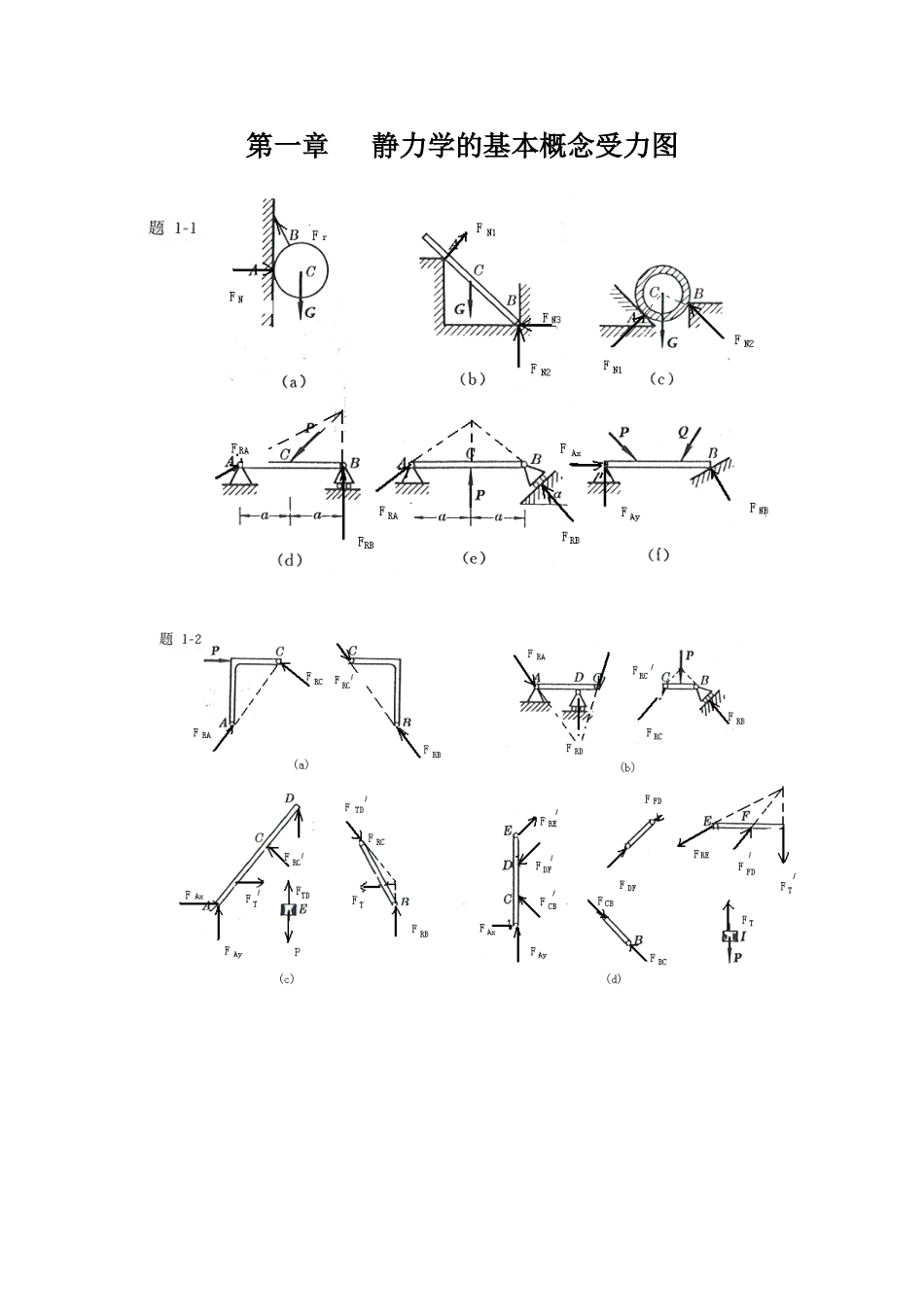
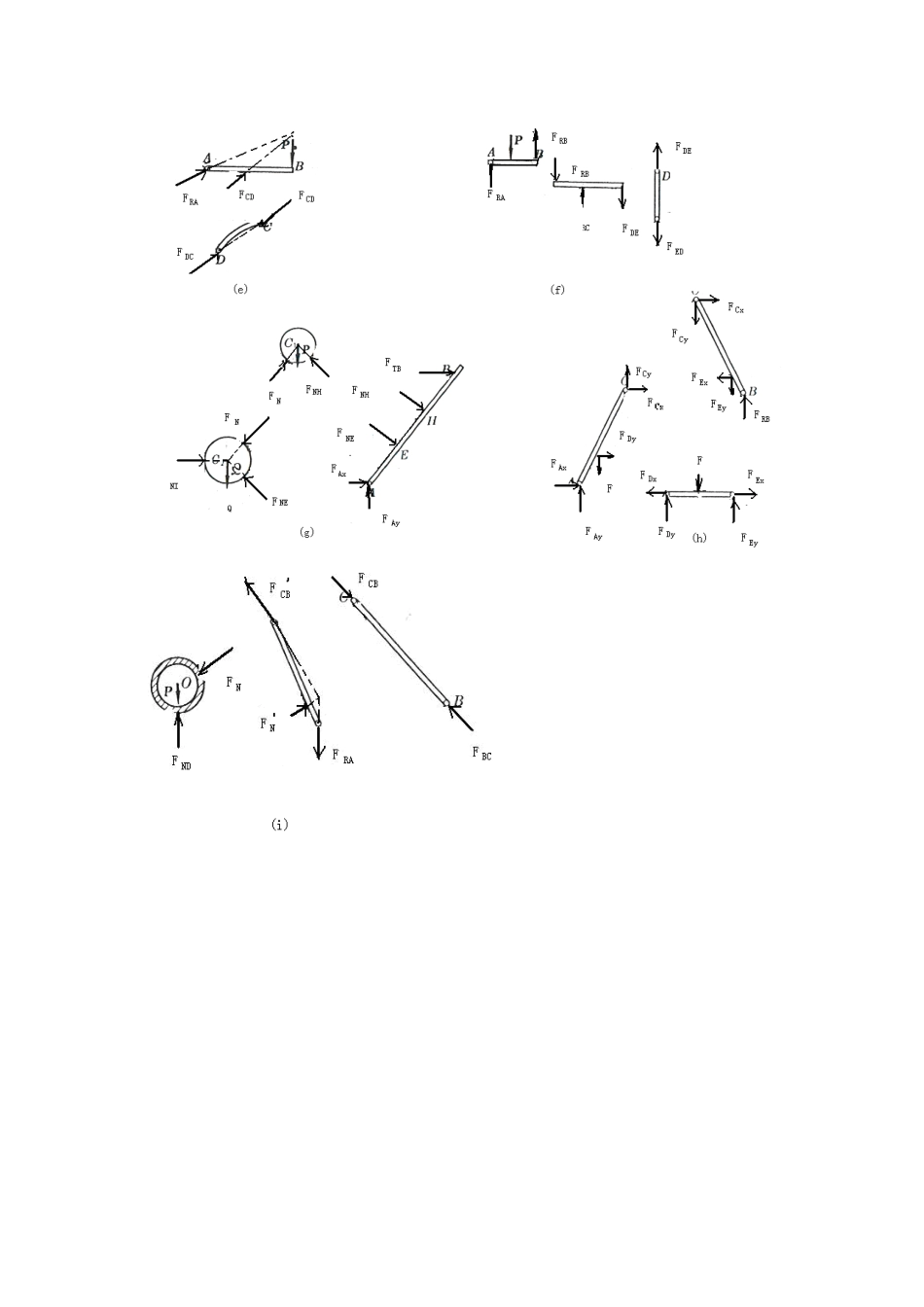
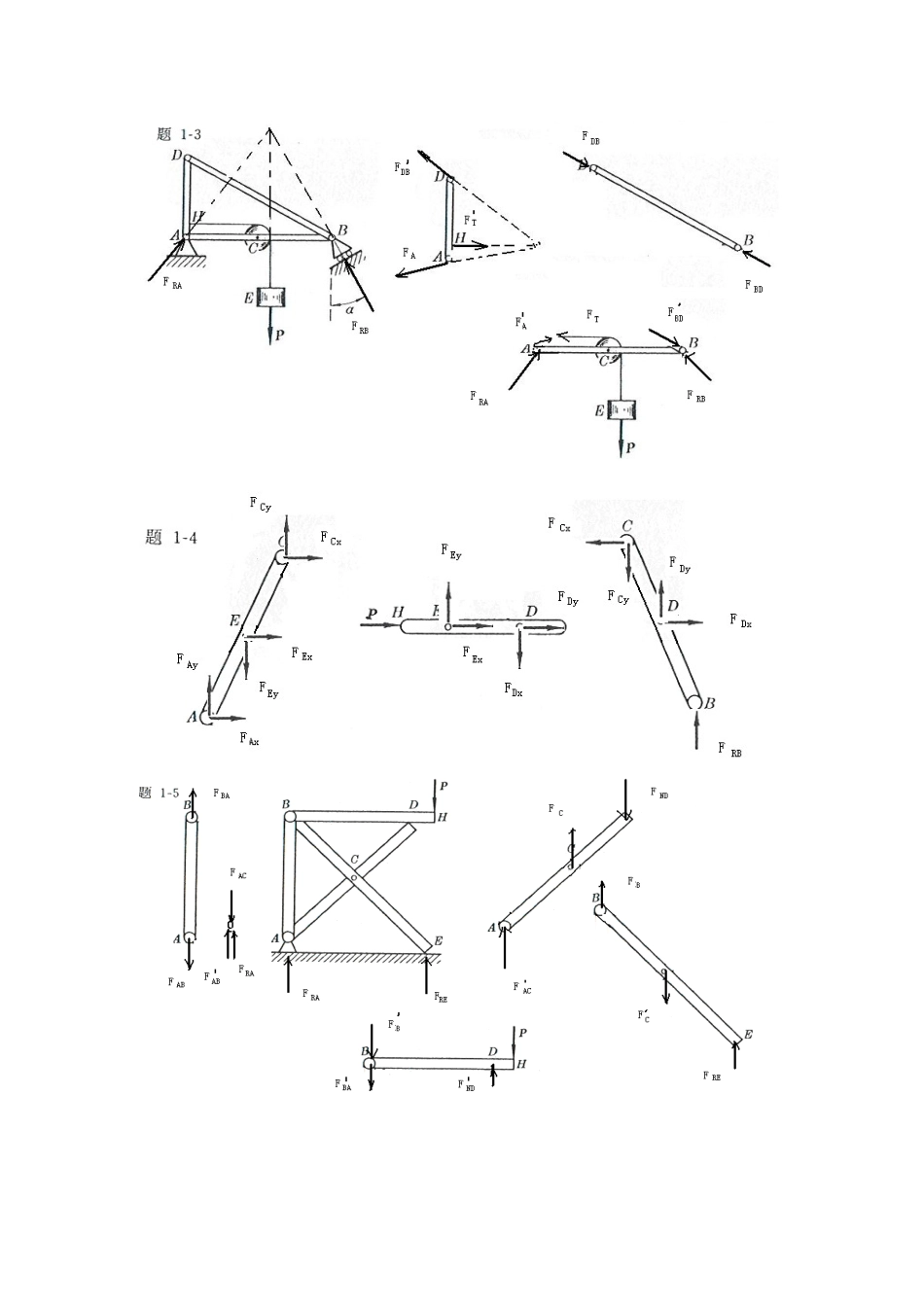
第一章静力学的基本概念受力图2-1解：由解析法，23cos80RXFXPPN12sin140RYFYPPN故：22161.2RRXRYFFFN1(,)arccos2944RYRRFFPF2-2解：即求此力系的合力，沿OB建立x坐标，由解析法，有123cos45cos453RXFXPPPKN13sin45sin450RYFYPP故：223RRXRYFFFKN方向沿OB。2-3解：所有杆件均为二力杆件，受力沿直杆轴线。（a）由平衡方程有：0Xsin300ACABFF0Ycos300ACFW0.577ABFW（拉力）1.155ACFW（压力）（b）由平衡方程有：0Xcos700ACABFF0Ysin700ABFW1.064ABFW（拉力）0.364ACFW（压力）（c）由平衡方程有：0Xcos60cos300ACABFF0Ysin30sin600ABACFFW0.5ABFW(拉力)0.866ACFW（压力）（d）由平衡方程有：0Xsin30sin300ABACFF0Ycos30cos300ABACFFW0.577ABFW(拉力)0.577ACFW(拉力)2-4解：（a）受力分析如图所示：由0x224cos45042RAFP15.8RAFKN由0Y222sin45042RARBFFP7.1RBFKN(b)解：受力分析如图所示：由0x3cos45cos45010RARBFFP0Y1sin45sin45010RARBFFP联立上二式，得：22.410RARBFKNFKN2-5解：几何法：系统受力如图所示三力汇交于点D，其封闭的力三角形如图示所以：5RAFKN（压力）5RBFKN（与X轴正向夹150度）2-6解：受力如图所示：已知，1RFG，2ACFG由0xcos0ACrFF12cosGG由0Ysin0ACNFFW22221sinNFWGWGG2-7解：受力分析如图所示，取左半部分为研究对象由0xcos45cos450RACBPFF0Ysin45sin450CBRAFF联立后，解得：0.707RAFP0.707RBFP由二力平衡定理0.707RBCBCBFFFP2-8解：杆AB，AC均为二力杆，取A点平衡由0xcos60cos300ACABFFW0Ysin30sin600ABACFFW联立上二式，解得：7.32ABFKN（受压）27.3ACFKN（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D，B点分别列平衡方程（1）取D点，列平衡方程由0xsincos0DBTW0DBTWctg（2）取B点列平衡方程：由0Ysincos0BDTT230BDTTctgWctgKN2-10解：取B为研究对象：由0Ysin0BCFPsinBCPF取C为研究对象：由0xcossinsin0BCDCCEFFF由0Ysincoscos0BCDCCEFFF联立上二式，且有BCBCFF解得：2cos12sincosCEPF取E为研究对象：由0Ycos0NHCEFFCECEFF故有：22cos1cos2sincos2sinNHPPF2-11解：取A点平衡：0xsin75sin750ABADFF0Ycos75cos750ABADFFP联立后可得：2cos75ADABPFF取D点平衡，取如图坐标系：0xcos5cos800ADNDFFcos5cos80NDADFF由对称性及ADADFFcos5cos5222166.2cos80cos802cos75NNDADPFFFKN2-12解：整体受力交于O点，列O点平衡由0xcoscos300RADCFFP0Ysinsin300RAFP联立上二式得：2.92RAFKN1.33DCFKN（压力）列C点平衡0x405DCACFF0Y305BCACFF联立上二式得：1.67ACFKN（拉力）1.0BCFKN（压力）2-13解：（1）取DEH部分，对H点列平衡0x205RDREFF0Y105RDFQ联立方程后解得：5RDFQ2REFQ（2）取ABCE部分，对C点列平衡0xcos450RERAFF0Ysin450RBRAFFP且REREFF联立上面各式得：22RAFQ2RBFQP（3）取BCE部分。根据平面汇交力系平衡的几何条件。2222222284RCRERBFFFQQPQPQP2-14解：（1）对A球列平衡方程0xcossin0ABNAFF（1）0Ycossin20NAABFFP（2）（2）对B球列平衡方程0xcoscos0NBABFF（3）0Ysinsin0NBABFFP（4）且有：NBNBFF（5）把（5）代入（3），（4）由（1），（2...