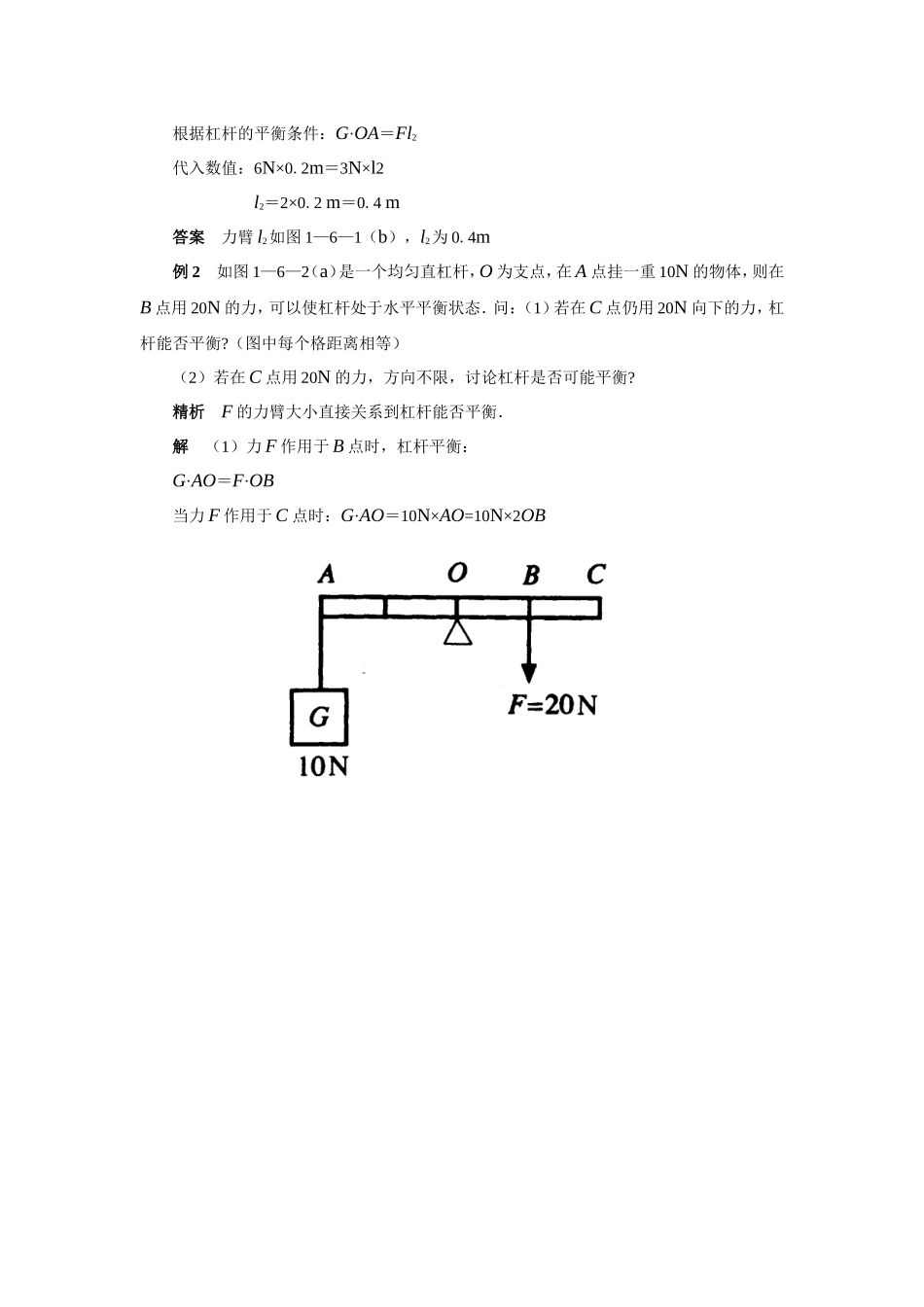
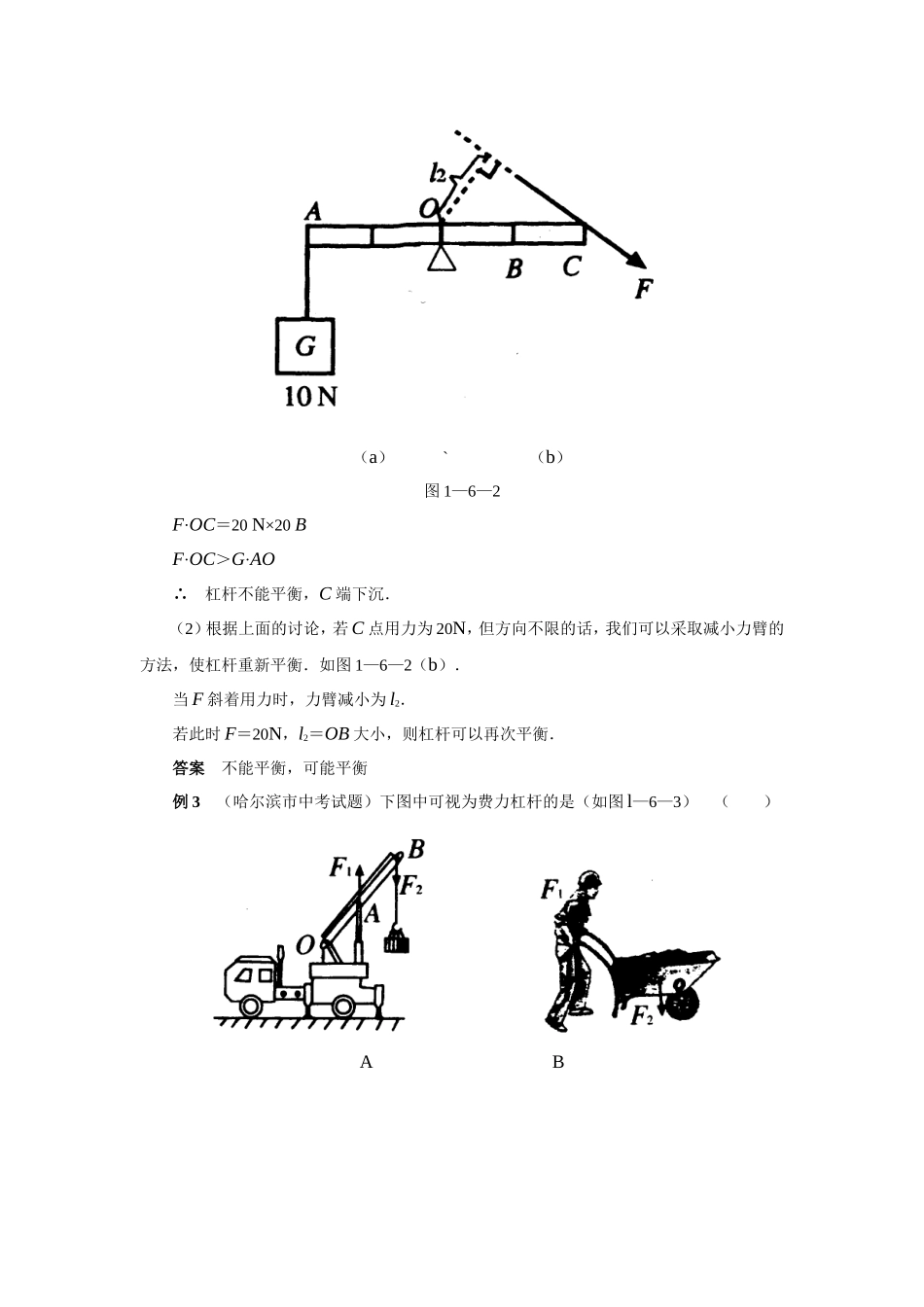
典型例题解析例1(镇江市中考试题)如图1—6—1(a)所示的杠杆重;不计,O为支点,AO=0.2m,当在A点悬吊一重6N的物体,绳子的拉力F=3N时,杠杆在水平位置平衡,在图中画出拉力矿的力臂l2,力臂l2为________m.(a)`(b)图1—6—1如图1—6—1(b),画出杠杆OAB示意图,找到支点O,BC为力的作用线,画出力臂l2.根据杠杆的平衡条件:G·OA=Fl2代入数值:6N×0.2m=3N×l2l2=2×0.2m=0.4m答案力臂l2如图1—6—1(b),l2为0.4m例2如图1—6—2(a)是一个均匀直杠杆,O为支点,在A点挂一重10N的物体,则在B点用20N的力,可以使杠杆处于水平平衡状态.问:(1)若在C点仍用20N向下的力,杠杆能否平衡?(图中每个格距离相等)(2)若在C点用20N的力,方向不限,讨论杠杆是否可能平衡?精析F的力臂大小直接关系到杠杆能否平衡.解(1)力F作用于B点时,杠杆平衡:G·AO=F·OB当力F作用于C点时:G·AO=10N×AO=10N×2OB(a)`(b)图1—6—2F·OC=20N×20BF·OC>G·AO∴杠杆不能平衡,C端下沉.(2)根据上面的讨论,若C点用力为20N,但方向不限的话,我们可以采取减小力臂的方法,使杠杆重新平衡.如图1—6—2(b).当F斜着用力时,力臂减小为l2.若此时F=20N,l2=OB大小,则杠杆可以再次平衡.答案不能平衡,可能平衡例3(哈尔滨市中考试题)下图中可视为费力杠杆的是(如图l—6—3)()ABCD图1—6—3精析起重机,l1<l2,Fl>F2为费力杠杆.其他:手推车、瓶启子、撬杠均是l1>l2,为省力杠杆.答案A例4(乌鲁木齐市中考试题)如图1—6—4(a)所示,杠杆A处挂一重为40N的物体,杠杆在拉力F作用下保持平衡.O是杠杆的支点.请画出拉力F的力臂L.并写出杠杆平衡时的表达式.(a)(b)(c)(d)图1—6—4如图1—6—4(b)F的力臂为L.杠杆平衡时:G·OA=F·L.扩展:若CB>AO>OC,当F方向垂直于CB时,F的力臂为L′>OA,F<G.当F沿CB方向时,如图1—6—4(d).F的力臂为L″,当L″<OA时,F>G.答案如图1—6—4(b)(d),平衡时:G·OA=F·L例5(苏州市中考题)杠杆OA在力FA、FB的作用下保持水平静止状态,如图1—6—5(a).杠杆的自重不计,O为杠杆的支点,FB的方向与OA垂直,则下列关系式中一定正确的是()A.FA·OA=FB·OBB.FA·OA<FB·OBC.=D.FA>(a)(b)图1—6—5精析此题是考查学生对杠杆平衡条件的理解和能否正确地找出力臂.如图1—6—5(b),画出力FA的力臂为lA,FA和OA的夹角为θ。根据杠杆的平衡条件:FA·lA=FB·OBFA·OAsinθ=FB·OB.从图中看出:0°<θ<90°∴sinθ<1要保持杠杆平衡:FA·OA>FB·OB,推得FA>答案D例6(长沙市中考试题)在图1—6—6(a)中,画出使用滑轮组提升重物时,绳子最省力的绕法.(a)(b)图1—6—6如图1—6—6(b),绳子的绕法为最省力,则应从定滑轮开始绕起,最后承担物重的绳子根数为4根.如何求滑轮组绳子上的拉力?(1)使用滑轮组竖直提起重物第一种情况,在忽略动滑轮重和摩擦及绳重等额外阻力时,绳子自由端拉力:F=.如图1—6—6(b),n=4,F=第二种情况,不计摩擦和绳重,但考虑动滑轮重.拉力:F=如图1—6—6(b),若物体重500N,动滑轮重100N,则拉力:F==150N.第三种情况,又要考虑动滑轮重,又要计摩擦等额外阻力,则应从机械效率去考虑求出拉力.公式推导:η==拉力:F=,如图1—6—6(b),若物体重500N,滑轮组机械效率为70%,s=4h,则拉力:F==≈178.6N(2)使用滑轮组平拉重物图1—6—7如图1—6—7,用滑轮组匀速拉动物体A,这时拉力F大小和重量无直接关系.在不计滑轮重,滑轮摩擦等额外阻力时,拉力:F==,其中f表示A与地面的摩力.n表示与动滑轮连接的绳子根数.设:A重120N,A与地面摩擦力为30N,则拉力:F==10N.例7(南京市中考试题)利用图1—6—8中的滑轮组提升重物A(物体A重1600N),滑轮组的机械效率为80%,当物体匀速提升时,作用在绳端的拉力F为________N,如果增大物重,此滑轮组的机械效率.(选填“变大”、“变小”或“不变”)图1—6—8精析考查力、功和机械效率之间的关系.解已知:G=1600N,机械效率η=80%设提升时,物体上升h.根...