三角函数图像变换222VIP免费

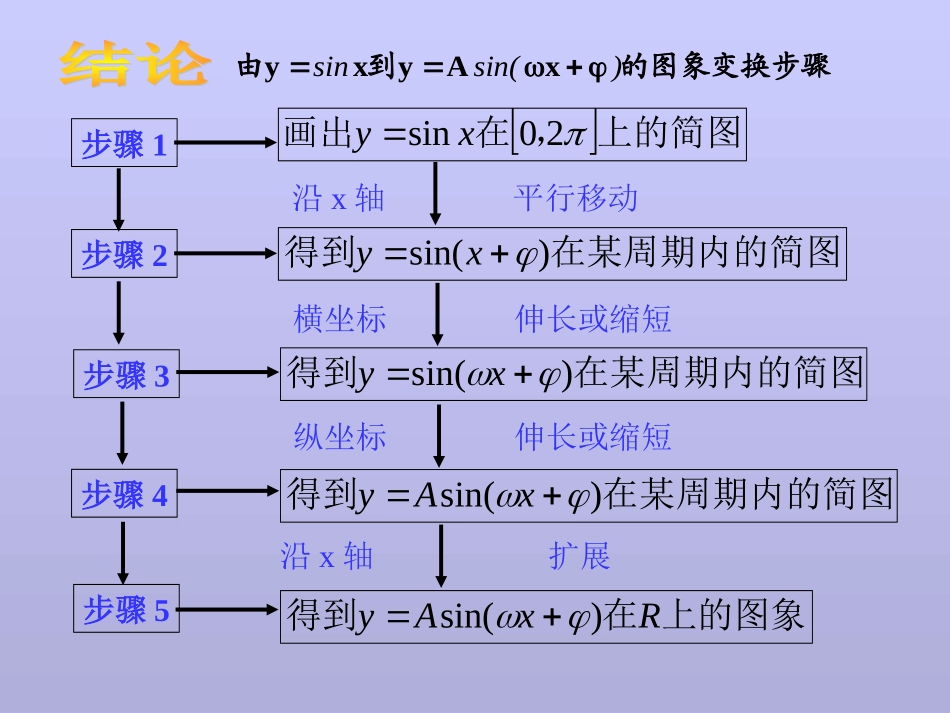
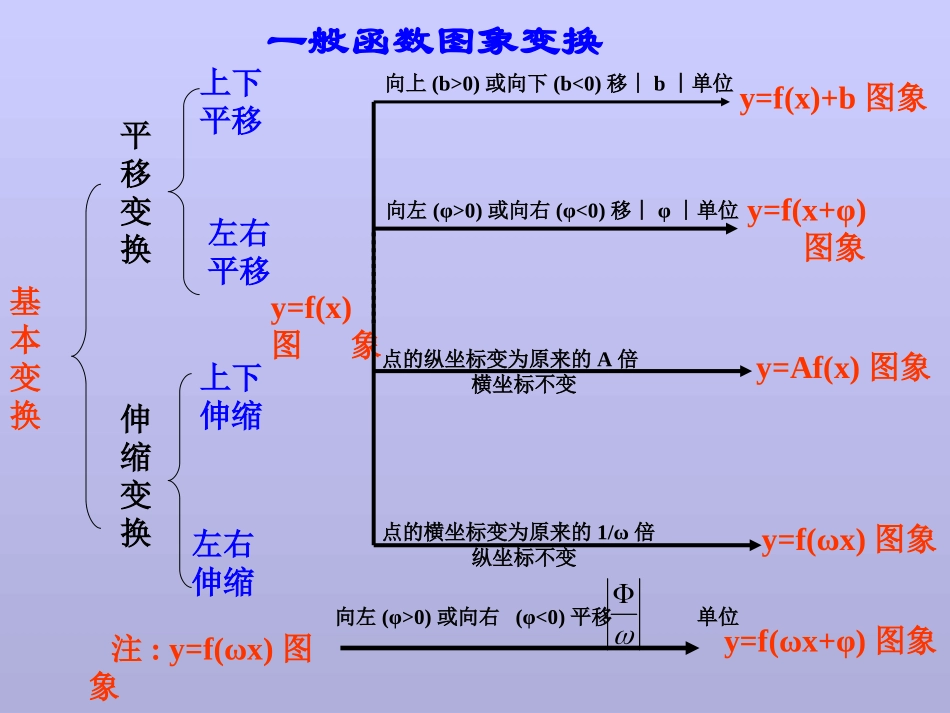
函数函数的图象和性质的图象和性质我们的目标1、掌握函数图象的平移、对称和伸缩变换的规律2、掌握正弦函数图象的相位、周期和振幅变换的规律3.掌握由图像写出三角函数表达式的一般方法，体会转化的思想方法)sin(xAy步骤1步骤2步骤3步骤4步骤5上的简图，在画出20sinxy在某周期内的简图得到)sin(xy在某周期内的简图得到)sin(xy在某周期内的简图得到)sin(xAy上的图象在得到RxAy)sin(沿x轴平行移动横坐标伸长或缩短纵坐标伸长或缩短沿x轴扩展的图象变换步骤到由)sin(sinxAyxy一般函数图象变换基本变换平移变换伸缩变换上下平移左右平移上下伸缩左右伸缩y=f(x)图象y=f(x)+b图象y=f(x+φ)图象y=Af(x)图象y=f(ωx)图象向上(b>0)或向下(b<0)移︱b︱单位向左(φ>0)或向右(φ<0)移︱φ︱单位点的横坐标变为原来的1/ω倍纵坐标不变点的纵坐标变为原来的A倍横坐标不变注:y=f(ωx)图象y=f(ωx+φ)图象向左(φ>0)或向右(φ<0)平移单位三角函数图象变换基本变换平移变换伸缩变换上下平移左右平移上下伸缩左右伸缩y=sin(x)图象y=sin(x)+b图象y=sin(x+φ)图象y=Asin(x)图象y=sin(ωx)图象向上(b>0)或向下(b<0)移︱b︱单位向左(φ>0)或向右(φ<0)移︱φ︱单位点的横坐标变为原来的1/ω倍纵坐标不变点的纵坐标变为原来的A倍横坐标不变注:y=sin(ωx)图象y=sin(ωx+φ)图象向左(φ>0)或向右(φ<0)平移单位练习1sin(6sin.yxyx1、将函数)的图象向平移个单位，可得到函数的图象sin(3sin(.6yxyx2、将函数)的图象向平移个单位，可得到函数)的图象6右6左练习2sin2sin.3yxyx1、将函数的图象上每一个点的坐标不变，坐标，可得到函数的图象2sin(5sin.yxyx2、将函数)图象上每一个点的坐标不变，坐标，可得到函数的图象倍伸长到原来的23纵横纵横52缩短到原来的练习3cos2cos.3yxyx1、将函数的图象上每一个点的坐标不变，坐标，可得到函数的图象2sin5sin.yxyx2、将函数图象上每一个点的坐标不变，坐标，可得到函数的图象横纵横纵倍伸长到原来的25倍缩短到原来的32：3x32xx2y、12填空已知函数例,coscossin13x2①振幅是:周期是:频率是:相位是:初相是:②定义域是:值域是:④递减区间是:_________________⑤图像的对称轴方程为:__________________;图像的对称中心为:__________________;⑥两相邻最大值之间的距离是:___________________;与x轴两相邻交点之间的距离为:___________________;最小值与相邻x轴交点之间的距离为:___________________。2π；yx③_______,_______________max时当3R[-2，2])(Zk12kx2)(,Zk］127k12k［)(Zk2k12xZ）k）（02k6（,π24.,.,sin,:叫做初相叫做相位叫做频率叫做周期叫做振幅其中的形式通常把原三角函数化为像和性质时在研究某些三角函数图解后反思x，2T1。2T，A00A，）x（Ay：3x32xx2y、12填空已知函数例,coscossin1.;1.;2.;2.)(82cos2sin.2.DCBAaxxaxy等于对称，那么π的图像关于直线如果函数例思路1:函数y=sin2x+acos2x可化为:)2sin(12φxay要使它的图象关于直线x=-π/8对称,则图象在该处必是处于波峰或波谷.即函数在x=-π/8时取得最大、小值.2a1)8(2cosa)8(2sin:｜ππ由｜解.D1a，应选解得对称的图象关于直线思路82xxfy)(:)cos()sin(cossin)()(220040aff即1a）（x2y，4x2y、3的图像只须将的图像要得到函数例sin)cos(8A、向左平移个单位4C、向左平移个单位D、向右平移个单位4B、向右平移个单位8—.—————)(;),()();cos()()()(：；6xxfy④06xfy③6x24yxfy②；xx，0xfxf①2121其中正确的例题是对称的图像关于直线对称的图像关于的表达式可改写为的整数倍必是可得由：Rx3x24xf、4有下列命题关于函数例),)(sin()(A②③。，xAy5求这个函数的解析式的图像的一部分图中曲线是函数例)sin(:32A：显然解析...