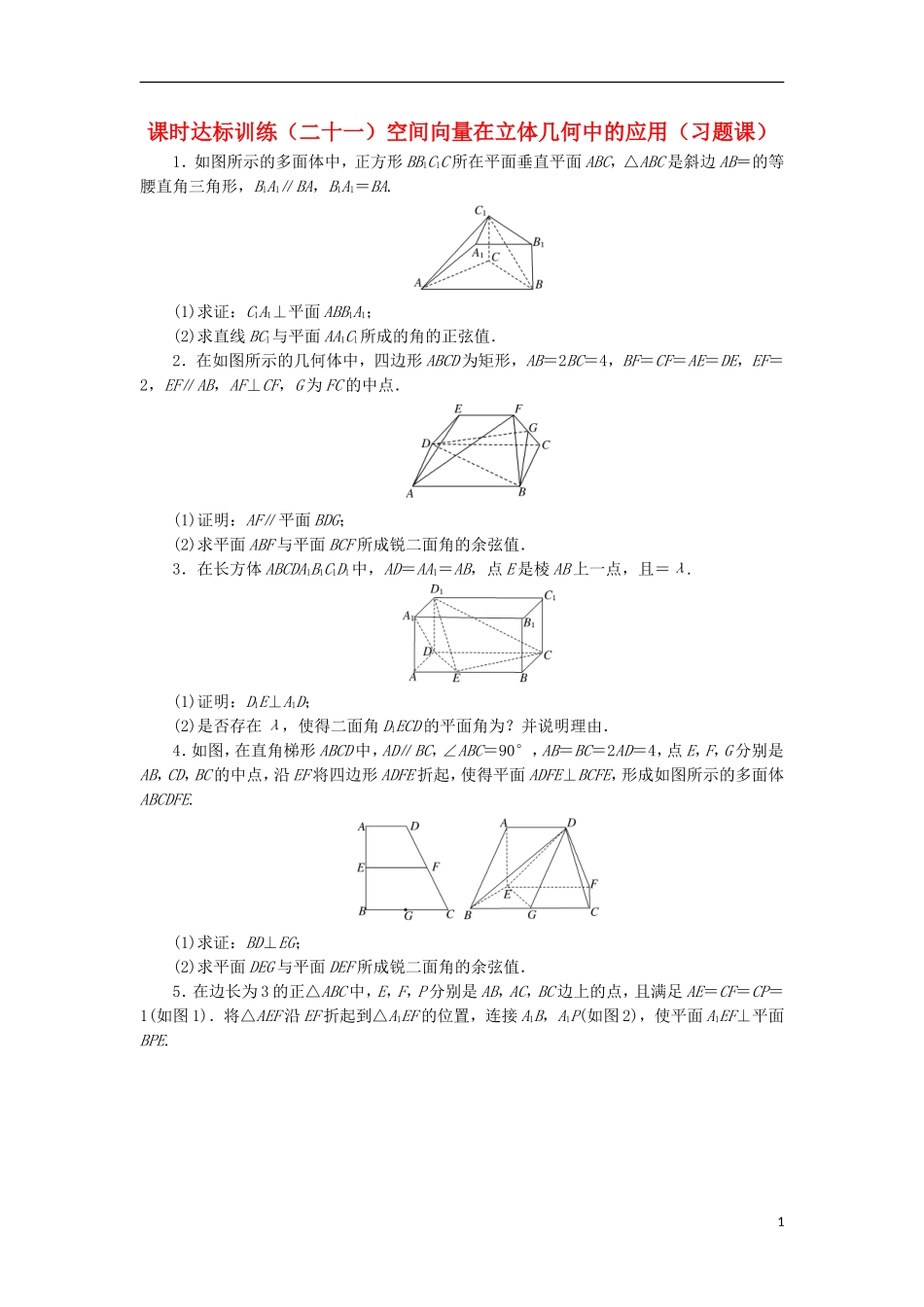
课时达标训练(二十一)空间向量在立体几何中的应用(习题课)1.如图所示的多面体中,正方形BB1C1C所在平面垂直平面ABC,△ABC是斜边AB=的等腰直角三角形,B1A1∥BA,B1A1=BA.(1)求证:C1A1⊥平面ABB1A1;(2)求直线BC1与平面AA1C1所成的角的正弦值.2.在如图所示的几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF,G为FC的中点.(1)证明:AF∥平面BDG;(2)求平面ABF与平面BCF所成锐二面角的余弦值.3.在长方体ABCDA1B1C1D1中,AD=AA1=AB,点E是棱AB上一点,且=λ.(1)证明:D1E⊥A1D;(2)是否存在λ,使得二面角D1ECD的平面角为?并说明理由.4.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD=4,点E,F,G分别是AB,CD,BC的中点,沿EF将四边形ADFE折起,使得平面ADFE⊥BCFE,形成如图所示的多面体ABCDFE.(1)求证:BD⊥EG;(2)求平面DEG与平面DEF所成锐二面角的余弦值.5.在边长为3的正△ABC中,E,F,P分别是AB,AC,BC边上的点,且满足AE=CF=CP=1(如图1).将△AEF沿EF折起到△A1EF的位置,连接A1B,A1P(如图2),使平面A1EF⊥平面BPE.1(1)求证:A1E⊥平面BEP;(2)求直线A1E与平面A1BP所成角的大小.6.如图,在直三棱柱ABCA1B1C1中,A1A⊥平面ABC,∠BAC=60°,A1A=4,AB=AC=2.F为棱AA1上的动点,D是BC1上的点且BD=DC1.(1)若DF∥平面ABC,求的值;(2)当的值为多少时,直线A1C1与平面BFC1所成角的正弦值为?答案1.解:易知CA,CB,CC1两两垂直,且CA=CB=CC1=1,故以C为原点,以CA为x轴建立空间直角坐标系如图所示,则A(1,0,0),B(0,1,0),C1(0,0,1),A1,∴C1A1⊥AA1,C1A1⊥AB.又 AA1∩AB=A,∴C1A1⊥平面ABB1A1.(2)设平面AA1C1的法向量为n=(x,y,z),令x=1,则n=(1,-1,1).又=(0,-1,1),设直线BC1与平面AA1C1所成的角为θ,22.解:(1)证明:连接AC交BD于O点,则O为AC的中点,连接OG, 点G为FC的中点,∴OG∥AF. AF⊄平面BDG,OG⊂平面BDG,∴AF∥平面BDG.(2)取AD的中点M,BC的中点Q,连接MQ,则MQ∥AB∥EF,∴M,Q,F,E共面.作FP⊥MQ于P,EN⊥MQ于N,则EN∥FP且EN=FP.连接EM,FQ, AE=DE=BF=CF,AD=BC,∴△ADE≌△BCF,∴EM=FQ,∴Rt△ENM≌Rt△FPQ,∴MN=PQ=1. BF=CF,Q为BC中点,∴BC⊥FQ.又BC⊥MQ,FQ∩MQ=Q,∴BC⊥平面MQFE,∴PF⊥BC,∴PF⊥平面ABCD.以P为原点,PM所在直线为x轴,PF所在直线为z轴建立空间直角坐标系,如图所示,则A(3,1,0),B(-1,1,0),C(-1,-1,0),设F(0,0,h)(h>0),则=(-3,-1,h),=(1,1,h). AF⊥CF,∴·=0,解得h=2.则=(-3,-1,2),=(1,-1,2),设平面ABF的法向量为n1=(x1,y1,z1),令z1=1,得x1=0,y1=2,∴n1=(0,2,1).同理得平面BCF的一个法向量为n2=(-2,0,1).∴|cos〈n1,n2〉|===,∴平面ABF与平面BCF所成锐二面角的余弦值为.3.解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,如图所示.3不妨设AD=AA1=1,AB=2,则D(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1).因为=λ,所以E,于是=,=(-1,0,-1),所以·=·(-1,0,-1)=-1+0+1=0,故D1E⊥A1D.(2)因为DD1⊥平面ABCD,所以平面DEC的一个法向量为n=(0,0,1),设平面D1EC的法向量为n1=(x,y,z),又=,=(0,-2,1),整理得取y=1,则n1=.因为二面角D1ECD的平面角为,所以=,即=,解得λ=-1.故存在λ=-1,使得二面角D1ECD的平面角为.4.解:(1) AD∥BC,BC=2AD=4,E,F分别是AB,CD的中点,∴AD∥EF,EF∥BC,EF=3. ∠ABC=90°,∴EF⊥AE,EF⊥BE,∴EF⊥平面AEB. 平面ADFE⊥平面BCFE,∴AE⊥EB,∴EB,EF,EA两两垂直.以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立如图所示的空间直角坐标系由已知得E(0,0,0),A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0),∴=(2,2,0),=(-2,2,2).∴·=-2×2+2×2=0,∴BD⊥EG.(2)由已知,得=(2,0,0)是平面DEF的一个法向量.设平面D...