3.3勾股定理的简单应用VIP免费

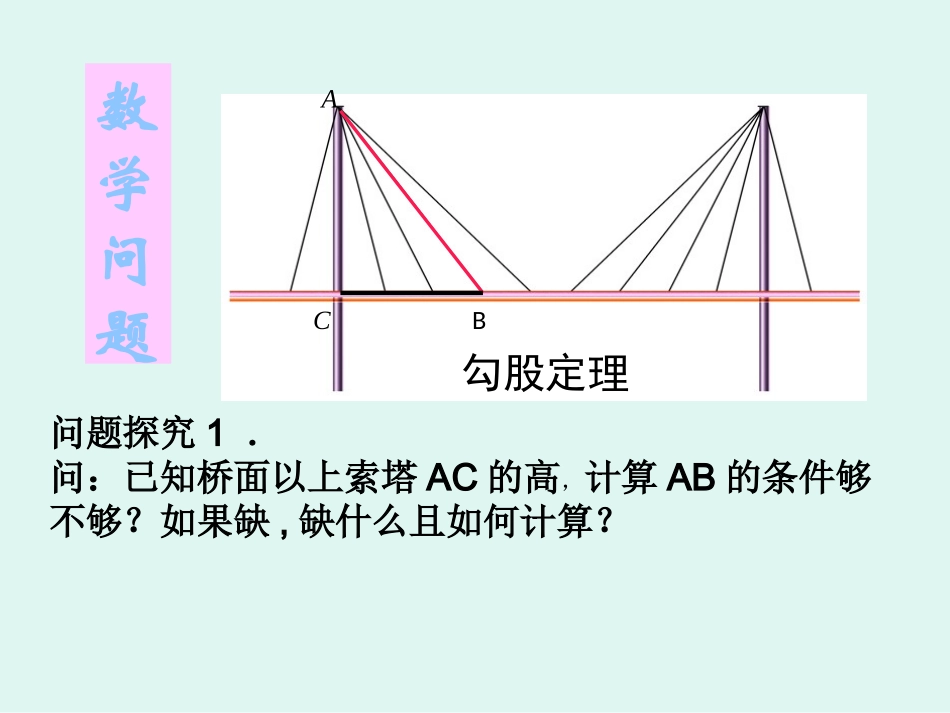
八年级(上册)初中数学3.3勾股定理的简单应用小明国庆去镇江经过润扬大桥，从远处看斜拉桥的索塔、桥面与拉索组成许多直角三角形．数学问题问题探究1．问：已知桥面以上索塔AC的高，计算AB的条件够不够？如果缺,缺什么且如何计算？ACB勾股定理•练习：•(1)若已知索塔AC=4,则BC=3,拉索AB=•(2))若已知索塔AC=6,拉索AB=10,则BC=•(3)若已知BC=5,拉索AB=13,则AC=3.3勾股定理的简单应用3.3勾股定理的简单应用5812问题探究2下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段.给一把卷尺你能想办法通过测量一些数据求出旗杆的高度吗?请你与同伴交流设计方案?小明通过测量发现旗杆上的绳子比旗杆多2米，当他把绳子的下端拉开6米后，发现下端刚好接触地面，你能帮他把旗杆的高度计算出来吗？ABC63.3勾股定理的简单应用3.3勾股定理的简单应用2.在直角三角形中，已知一边及另两边的数量关系，可以设一边为X,另一边用X的代数式表示，把三边代入勾股定理建立方程求出未知的边.，可求出第三边1.直角三角形中已知两边数学问题实际问题构造直角三角形经验方法：•《九章算术》中的“折竹”问题：今有竹高一丈，末折抵地，去根三尺，问折者高几何？3.3勾股定理的简单应用3.3勾股定理的简单应用问题引申：意思是：有一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？•.某工厂制作了一个直角三角形零件，经检测的三边分别为4m,5m,6m,.请问:这个零件是否合格?(是直角则合格,否则不合格)3.3勾股定理的简单应用3.3勾股定理的简单应用问题探究3：•.如图，有一块四边形的田ABCD，经检测∠B=90°，AB=3，BC=4，CD=12，AD=13，求这块田的面积.•.3.3勾股定理的简单应用3.3勾股定理的简单应用问题探究4：CDBA•如图，在△ABC中，AB＝13，BC＝10，BC边上的中线AD＝12，求AC．DCBA3.3勾股定理的简单应用3.3勾股定理的简单应用问题探究5：问题变式1：如图，在△ABC中，AB=AC=10,BC=12,求△ABC的面积3.3勾股定理的简单应用3.3勾股定理的简单应用•问题变式2如图，在△ABC中，AB＝15，BC＝14，AC＝13,求△ABC的面积。3.3勾股定理的简单应用3.3勾股定理的简单应用ABC•问题变式2如图，在△ABC中，AB＝15，BC＝14，AC＝13,求△ABC的面积。∵ADBC⊥ADB=ADC=90°∴∠∠∴AD2=AB2-BD2AD2=AC2-CD23.3勾股定理的简单应用3.3勾股定理的简单应用AD∴AB2-BD2=AC2-CD213∴152-x2=132–(14-x)2∴x=9BD=9∴∴AD2=AB2-BD2=144∴AD=12（负数舍去）∴△ABC的面积=BC×AD÷2=84解：作ADBC⊥，垂足为D设BD=x,则CD=14-xBC1514A一个门框的尺寸如图所示，一块长3m、宽2.4m的薄木板薄木板能否从门框内通过?为什么?ABCD1.5m2m薄木板薄木板2.4m3m