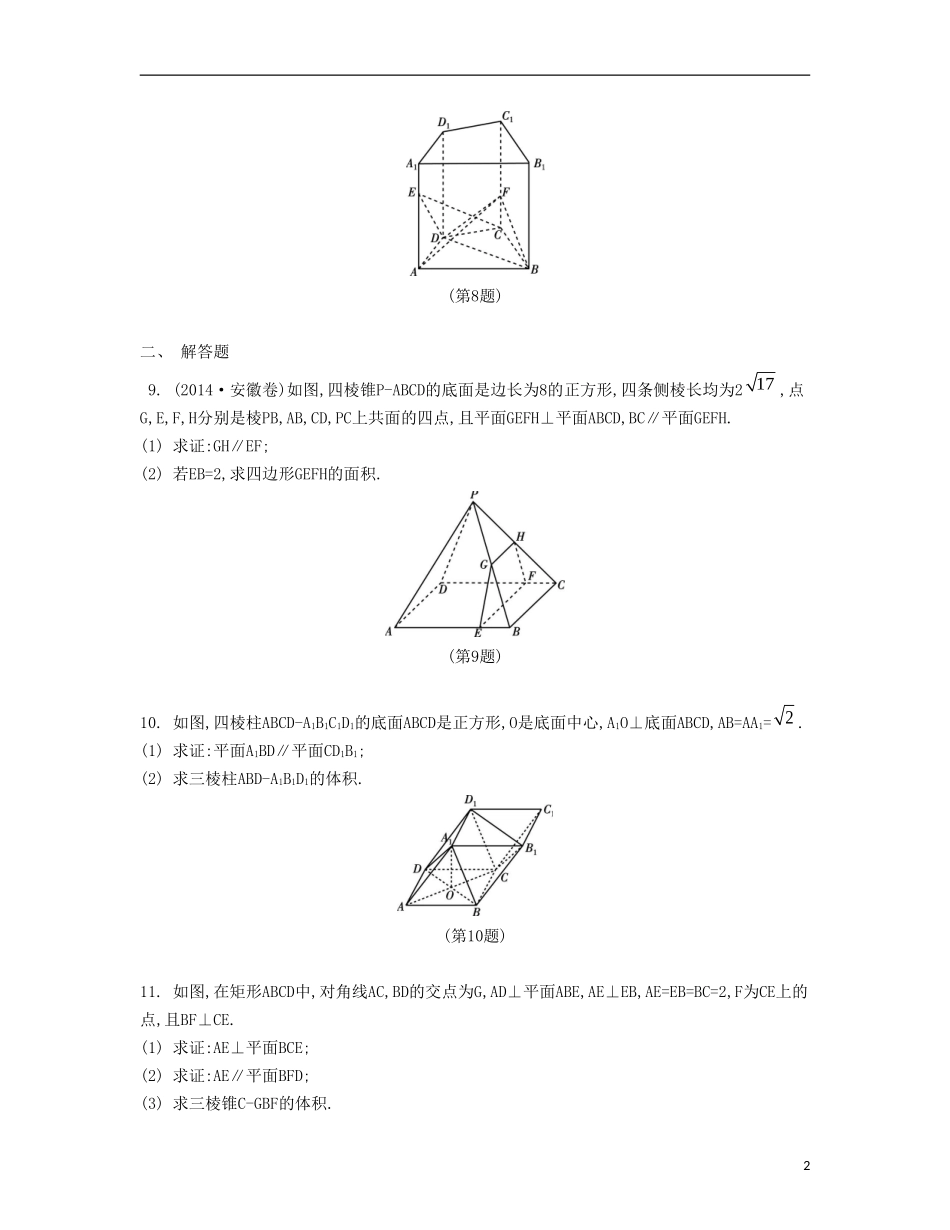
第53课空间几何体的表面积与体积一、填空题1.若一个长方体的长、宽、高分别为3,2,1,则它的外接球的表面积是.2.若正四棱锥的底面边长为6,高为7,则这个正四棱锥的侧面积是.3.(2014·福建卷)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于.4.(2014·山东卷)若一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为.5.(2014·全国卷)已知正四棱锥的顶点都在同一个球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为.6.已知正四棱锥O-ABCD的体积为322,底面边长为3,那么以O为球心、OA为半径的球的表面积为.7.如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上,则当PD=2AB=2,且APEDV=13时,PEEB的值为.(第7题)8.(2014·苏州模拟)如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=34AA1,CF=13CC1,点A,C到BD的距离之比为3∶2,则三棱锥E-BCD与F-ABD的体积之比为.1(第8题)二、解答题9.(2014·安徽卷)如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,且平面GEFH⊥平面ABCD,BC∥平面GEFH.(1)求证:GH∥EF;(2)若EB=2,求四边形GEFH的面积.(第9题)10.如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=2.(1)求证:平面A1BD∥平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.(第10题)11.如图,在矩形ABCD中,对角线AC,BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE.(1)求证:AE⊥平面BCE;(2)求证:AE∥平面BFD;(3)求三棱锥C-GBF的体积.2(第11题)3第53课空间几何体的表面积与体积1.6π2.483.2π解析:由题意知,所得圆柱的底面半径和高均为1,所以圆柱的侧面积为2π.4.12解析:设六棱锥的高为h,则V=13Sh,所以13×34×4×6h=23,解得h=1,设斜高为h',则h2+(3)2=h'2,解得h'=2,所以该六棱锥的侧面积为12×2×2×6=12.5.814解析:如图,因为正四棱锥的底面边长为2,所以AE=12AC=2.设球心为O,球的半径为R,则OE=4-R,OA=R,由△AOE为直角三角形,得OA2=OE2+AE2,即R2=(4-R)2+2,解得R=94,所以球的表面积S=4πR2=4π×294=814.(第5题)6.24π解析:设点O到底面的距离为h,则13×3×h=322,解得h=322,OA=2262h=6,故球的表面积为4π×(6)2=24π.7.1解析:设AC∩BD=O,由AO⊥BD,PD⊥AO,得AO⊥平面PDE,由题意得AO=1,则APEDV=13·AO·S△PDE=13,所以S△PDE=1,在Rt△PDB中,DB=PD=2,则PB=22,S△PDB=2,所以S△BDE=1,所以PEEB=PDEBDESS=41.8.32解析:点A,C到BD的距离之比为3∶2,所以BCDABDSS=23,在直四棱柱ABCD-A1B1C1D1中,AE=34AA1,CF=13CC1,所以AECF=94,于是EBCDFABDVV=1313BCDABDSAESCF=23×94=32.9.(1)因为BC∥平面GEFH,BC平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.同理可证EF∥BC,因此GH∥EF.(第9题)(2)如图,连接AC,BD交于点O,BD交EF于点K,连接OP,GK.因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.又BD∩AC=O,且AC,BD都在底面上,所以PO⊥底面ABCD.又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,所以PO∥平面GEFH.因为平面PBD∩平面GEFH=GK,所以PO∥GK,且GK⊥底面ABCD,从而GK⊥EF.所以GK是梯形GEFH的高.由AB=8,EB=2,得EB∶AB=KB∶DB=1∶4,从而KB=14DB=12OB,即K为OB的中点.再由PO∥GK得GK=12PO,即G是PB的中点,且GH=12BC=4.由已知可得OB=42,PO=22-PBOB=68-32=6,所以GK=3,所以四边形GEFH的面积S=2GHEF×GK=482×3=18.10.(1)由题设知,BB1DD1,所以四边形BB1D1D是平行四边形,所以BD∥B1D1.又BD⊄平面CD1B1,B1D1平面CD1B1,所以BD∥平面CD1B1.因为A1D1B1C1BC,所以四边形A1BCD1是平行四边形,5所以A1B∥D1C.又A1B⊄平面CD1B1,D1C平面CD1B1,所以A1B∥平面CD1B1.又因为BD∩A1B=B,所以平面A1BD∥平面CD1B1.(2)因为A1O⊥平面ABCD,所以A1O是三棱柱ABD-A1B1D1的高.又因为AO=12AC=1,AA1=2,所以A1O=221-AAOA=1,又因为S△ABD=12×2×2=1,所以三棱柱ABD-A1B1D1的体积V=S△ABD·A1O=1.11.(1)因为AD⊥平面ABE,AD∥BC,所以BC⊥平面ABE,又因为AE平面ABE,所以AE⊥BC.又因为AE⊥EB,BC∩EB=B,所以AE⊥平面BCE.(2)在矩形ABCD中,G是AC中点.因为EB=BC且BF⊥CE.所以F是EC中点,所以在△AEC中,FG∥AE.又因为FG平面BFD,AE⊄平面BFD,所以AE∥平面BFD.(3)因为F,G分别是EC,AC的中点,所以FG∥AE,且FG=12AE=1.因为AE⊥平面BCE,所以FG⊥平面BCE.在Rt△BCE中,EB=BC=2,F是EC中点,所以S△BCF=12S△BCE=12×12×BE×BC=1,所以CGBFV=GCFBV=13×S△CFB×FG=13.67