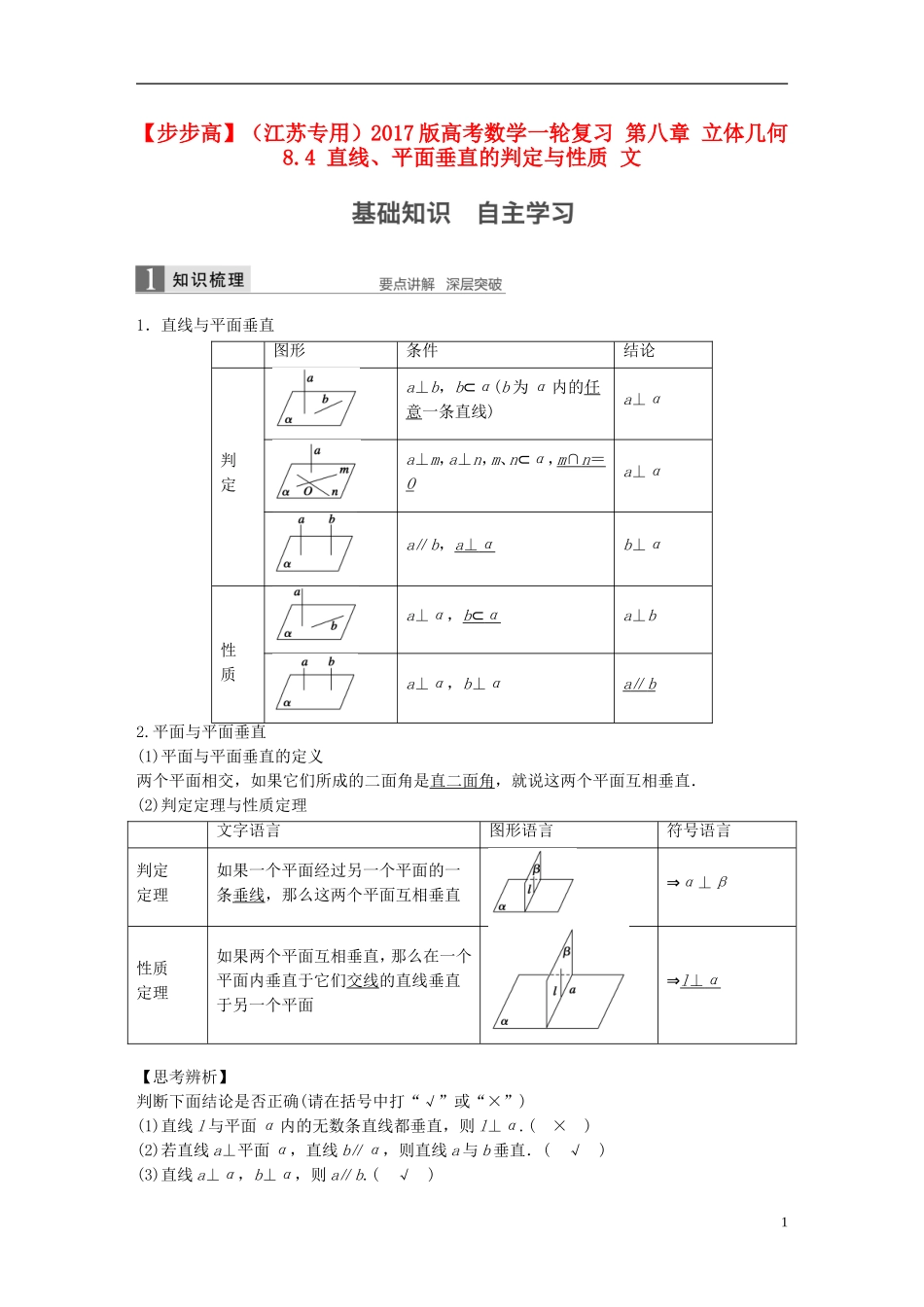
【步步高】(江苏专用)2017版高考数学一轮复习第八章立体几何8.4直线、平面垂直的判定与性质文1.直线与平面垂直图形条件结论判定a⊥b,b⊂α(b为α内的任意一条直线)a⊥αa⊥m,a⊥n,m、n⊂α,m∩n=Oa⊥αa∥b,a⊥αb⊥α性质a⊥α,b⊂αa⊥ba⊥α,b⊥αa∥b2.平面与平面垂直(1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理与性质定理文字语言图形语言符号语言判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直⇒α⊥β性质定理如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面⇒l⊥α【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)直线l与平面α内的无数条直线都垂直,则l⊥α.(×)(2)若直线a⊥平面α,直线b∥α,则直线a与b垂直.(√)(3)直线a⊥α,b⊥α,则a∥b.(√)1(4)若α⊥β,a⊥β⇒a∥α.(×)(5)a⊥α,a⊂β⇒α⊥β.(√)(6)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.(×)1.(教材改编)下列条件中,能判定直线l⊥平面α的是____________.①l与平面α内的两条直线垂直;②l与平面α内无数条直线垂直;③l与平面α内的某一条直线垂直;④l与平面α内任意一条直线垂直.答案④解析由直线与平面垂直的定义,可知④正确.2.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的____________条件.答案充分不必要解析若α⊥β,因为α∩β=m,b⊂β,b⊥m,所以根据两个平面垂直的性质定理可得b⊥α,又a⊂α,所以a⊥b;反过来,当a∥m时,因为b⊥m,且a,m共面,一定有b⊥a,但不能保证b⊥α,所以不能推出α⊥β.3.已知平面α⊥β,α∩β=l,P是空间一点,且P到平面α、β的距离分别是1、2,则点P到l的距离为________.答案解析如图, PO⊂平面PAB,∴l⊥PO.∴PO就是P到直线l的距离, α⊥β,∴四边形PAOB为矩形,PO==.4.(教材改编)PD垂直于正方形ABCD所在的平面,连结PB,PC,PA,AC,BD,则一定互相垂直的平面有________________________________________________________________________对.答案7解析由于PD⊥平面ABCD,故平面PAD⊥平面ABCD,平面PDB⊥平面ABCD,平面PDC⊥平面ABCD,平面PDA⊥平面PDC,平面PAC⊥平面PDB,平面PAB⊥平面PAD,平面PBC⊥平面PDC,共7对.5.(教材改编)在三棱锥P-ABC中,点P在平面ABC中的射影为点O,(1)若PA=PB=PC,则点O是△ABC的________心.(2)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的________心.答案(1)外(2)垂解析(1)如图1,连结OA,OB,OC,OP,在Rt△POA、Rt△POB和Rt△POC中,PA=PC=PB,所以OA=OB=OC,即O为△ABC的外心.2(2)如图2,延长AO、BO、CO分别交对边于H、D、G点, PC⊥PA,PB⊥PC,PA∩PB=P,∴PC⊥平面PAB,AB⊂平面PAB,∴PC⊥AB,又AB⊥PO,PO∩PC=P,∴AB⊥平面PGC,又CG⊂平面PGC,∴AB⊥CG,即CG为△ABC边AB的高.同理可证BD,AH为△ABC底边上的高,即O为△ABC的垂心.题型一直线与平面垂直的判定与性质例1(2014·辽宁)如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(1)求证:EF⊥平面BCG;(2)求三棱锥D-BCG的体积.(1)证明由已知得△ABC≌△DBC,因此AC=DC.又G为AD的中点,所以CG⊥AD.同理BG⊥AD,又BG∩CG=G,因此AD⊥平面BGC.又因E,F分别为AC,DC的中点,所以EF∥AD,所以EF⊥平面BCG.(2)解在平面ABC内,作AO⊥BC,交CB的延长线于O,如图由平面ABC⊥平面BCD,知AO⊥平面BDC.又G为AD中点,因此G到平面BDC的距离h是AO长度的一半.在△AOB中,AO=AB·sin60°=,所以VD-BCG=VG-BCD=S△DBC·h=×BD·BC·sin120°·=.思维升华(1)证明直线和平面垂直的常用方法:①判定定理;②垂直于平面的传递性(a∥b,a⊥α⇒b⊥α);③面面平行的性质(a⊥α,α∥β⇒a⊥β);④面面垂直的性质.(2)证明线面垂直的核心是证线线垂直,而证明线线垂直则需借助线面垂直的性质.因此,判定定理与性质定理的合...