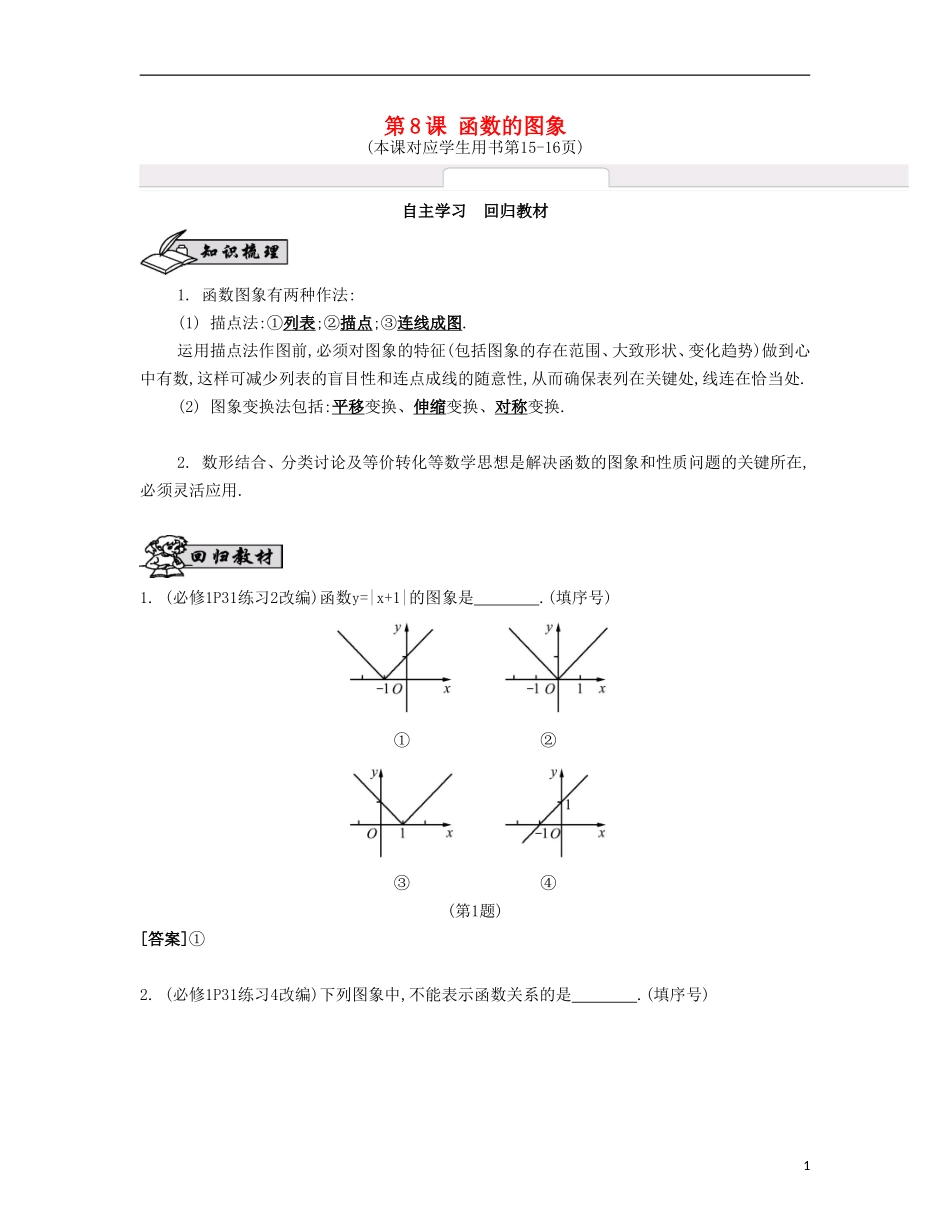
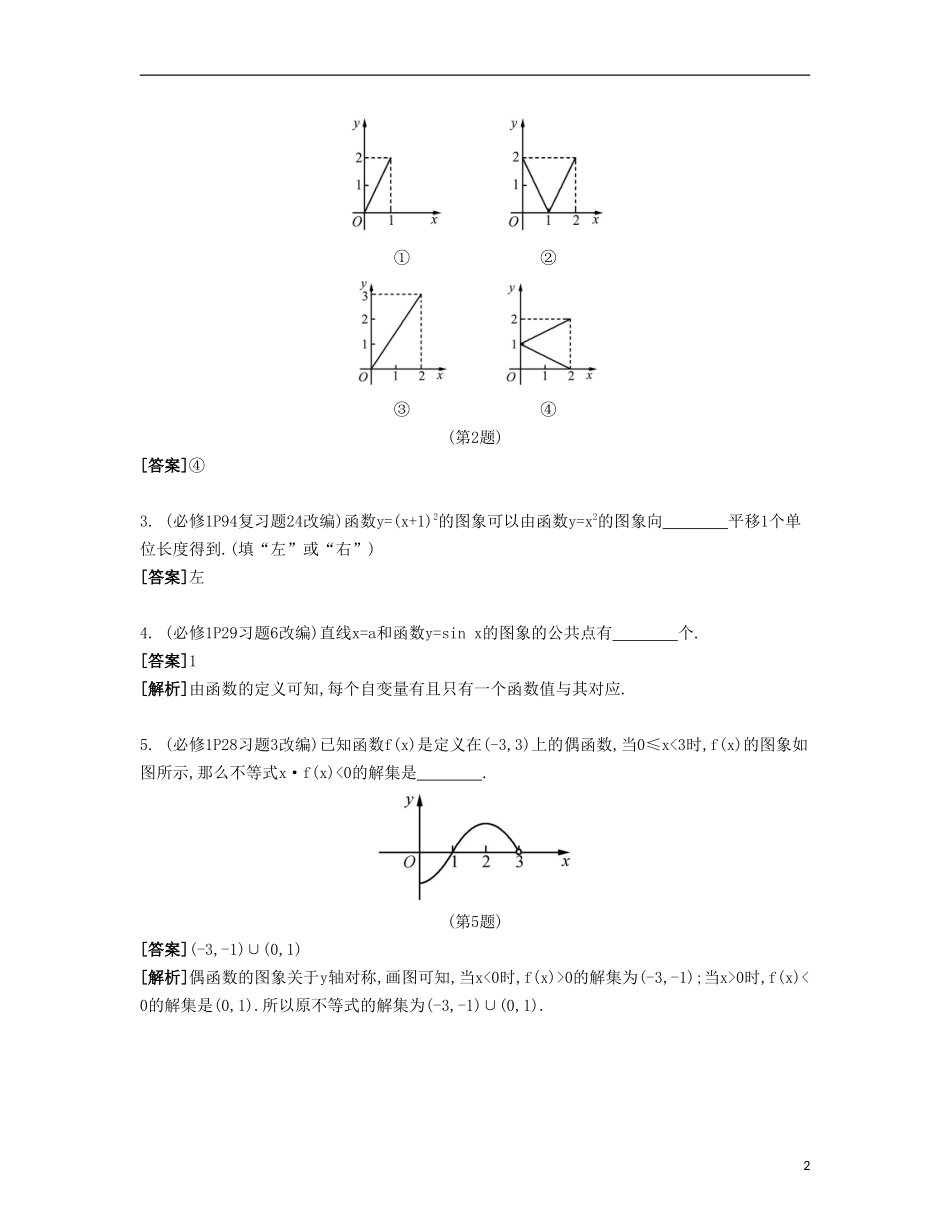
第8课函数的图象(本课对应学生用书第15-16页)自主学习回归教材1.函数图象有两种作法:(1)描点法:①列表;②描点;③连线成图.运用描点法作图前,必须对图象的特征(包括图象的存在范围、大致形状、变化趋势)做到心中有数,这样可减少列表的盲目性和连点成线的随意性,从而确保表列在关键处,线连在恰当处.(2)图象变换法包括:平移变换、伸缩变换、对称变换.2.数形结合、分类讨论及等价转化等数学思想是解决函数的图象和性质问题的关键所在,必须灵活应用.1.(必修1P31练习2改编)函数y=|x+1|的图象是.(填序号)①②③④(第1题)[答案]①2.(必修1P31练习4改编)下列图象中,不能表示函数关系的是.(填序号)1①②③④(第2题)[答案]④3.(必修1P94复习题24改编)函数y=(x+1)2的图象可以由函数y=x2的图象向平移1个单位长度得到.(填“左”或“右”)[答案]左4.(必修1P29习题6改编)直线x=a和函数y=sinx的图象的公共点有个.[答案]1[解析]由函数的定义可知,每个自变量有且只有一个函数值与其对应.5.(必修1P28习题3改编)已知函数f(x)是定义在(-3,3)上的偶函数,当0≤x<3时,f(x)的图象如图所示,那么不等式x·f(x)<0的解集是.(第5题)[答案](-3,-1)∪(0,1)[解析]偶函数的图象关于y轴对称,画图可知,当x<0时,f(x)>0的解集为(-3,-1);当x>0时,f(x)<0的解集是(0,1).所以原不等式的解集为(-3,-1)∪(0,1).2第8课函数的图象1.31解析:函数y=lgx310可化为y=lg(x+3)-1.2.①③④3.①4.④解析:只有选项④符合,此时0