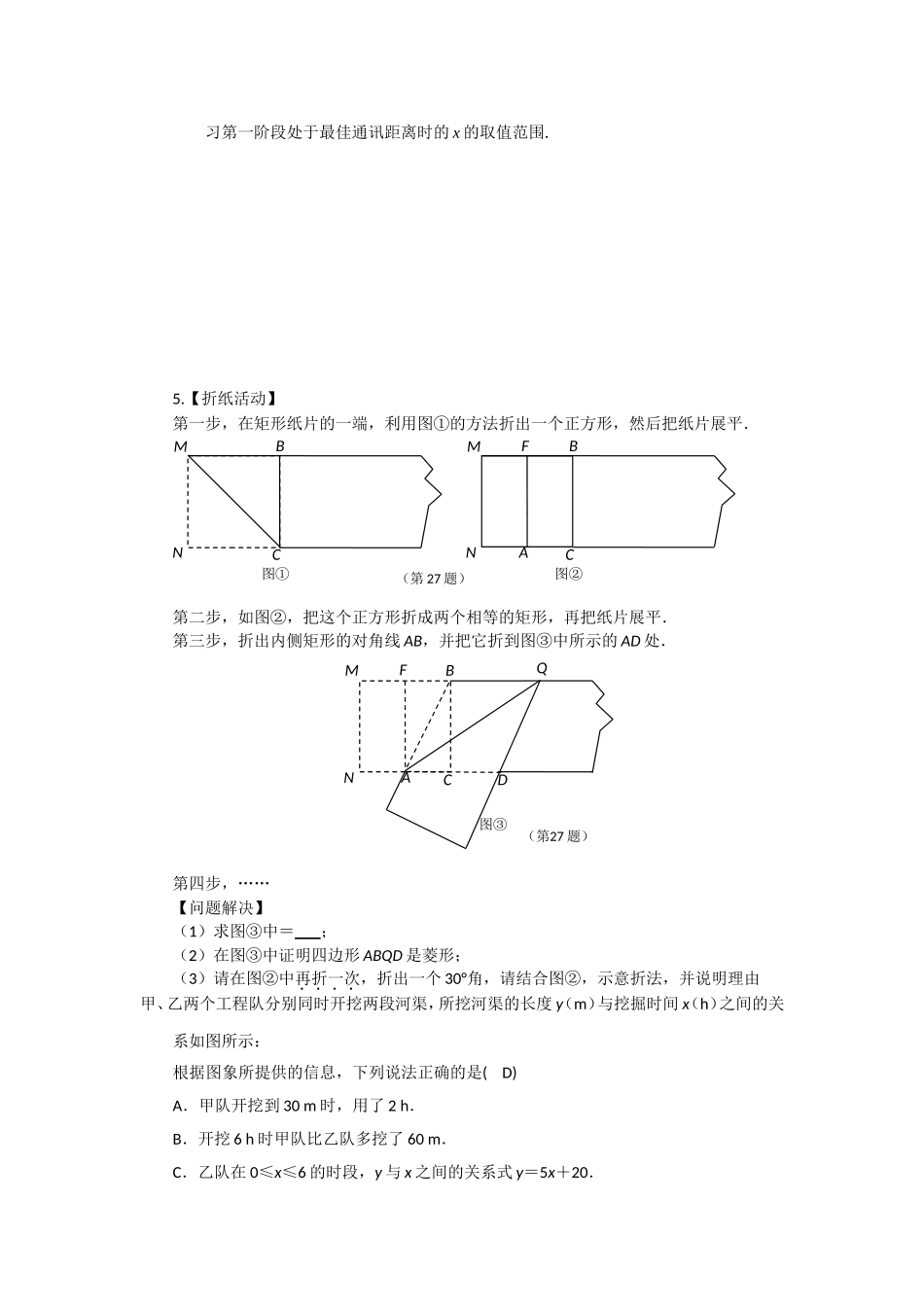
4月3日培优练习1.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示:根据图象所提供的信息,下列说法正确的是()A.甲队开挖到30m时,用了2h.B.开挖6h时甲队比乙队多挖了60m.C.乙队在0≤x≤6的时段,y与x之间的关系式y=5x+20.D.x为4h时,甲、乙两队所挖的河渠长度相等.2.小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为ym.图中折线段OBA表示小亮在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).(1)点B所表示的实际意义是;(2)求出AB所在直线的函数关系式;(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?3.甲、乙两车同时从M地出发,以各自的速度匀速向N地行驶.甲车先到达N地,停留1h后按原路以原速匀速返回,直到两车相遇,乙车的速度为50km/h.如图是两车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.(1)甲车的速度是km/h,M、N两地之间相距km;(2)求两车相遇时乙车行驶的时间;(3)求线段AB所在直线解析式.4.某次海军舰艇演习中,甲、乙两舰艇同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束.已知B港位于A港、C岛之间,且A、B、C在一条直线上.设甲、乙两舰艇行驶x(h)后,与B港的距离分别为y1和y2(km),y1、y2与x的函数关系如图所示.(1)求A港与C岛之间的距离;(2)分别求出甲、乙两舰艇的航速及图中点M的坐标;(3)若甲、乙两舰艇之间的距离不超过20km时就属于最佳通讯距离,试求出两舰艇在演(第9题)甲50Oy(m)x(h)302660乙x/miny/mOBA4802(第26题)x/hy/kmOA4B100ty2y12230.540160My/kmx/h习第一阶段处于最佳通讯距离时的x的取值范围.5.【折纸活动】第一步,在矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线AB,并把它折到图③中所示的AD处.第四步,……【问题解决】(1)求图③中=;(2)在图③中证明四边形ABQD是菱形;(3)请在图②中再折一次,折出一个30°角,请结合图②,示意折法,并说明理由甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示:根据图象所提供的信息,下列说法正确的是(D)A.甲队开挖到30m时,用了2h.B.开挖6h时甲队比乙队多挖了60m.C.乙队在0≤x≤6的时段,y与x之间的关系式y=5x+20.M图①NBCM图②NBCAFM图③NBCAFQD(第27题)(第27题)D.x为4h时,甲、乙两队所挖的河渠长度相等.小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为ym.图中折线段OBA表示小亮在整个训练中y与x的函数关系,其中点A在x轴上,点B坐标为(2,480).(1)点B所表示的实际意义是▲;(2)求出AB所在直线的函数关系式;(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?▲▲▲(1)小亮出发2分钟跑到坡顶,此时离坡脚480米;2分(2)小亮上坡的平均速度为480÷2=240(m/min)则其下坡的平均速度为240×1.5=360(m/min),故回到出发点时间为2+480÷360=(min),所以A点坐标为(,0),4分设y=kx+b,将B(2,480)与A(,0)代入,得,解得.所以y=-360x+1200.6分(3)小刚上坡的平均速度为240×0.5=120(m/min),小亮的下坡平均速度为240×1.5=360(m/min),由图像得小亮到坡顶时间为2分钟,此时小刚还有480-2×120=240m没有跑完,8分两人第一次相遇时间为2+240÷(120+360)=2.5(min).(或求出小刚的函数关系式y=120x,再与y=-360x+1200联立方程组,求出x=2.5也可以.)10分甲、乙两车同时从M地出发,以各自的速度匀速向N地行驶....