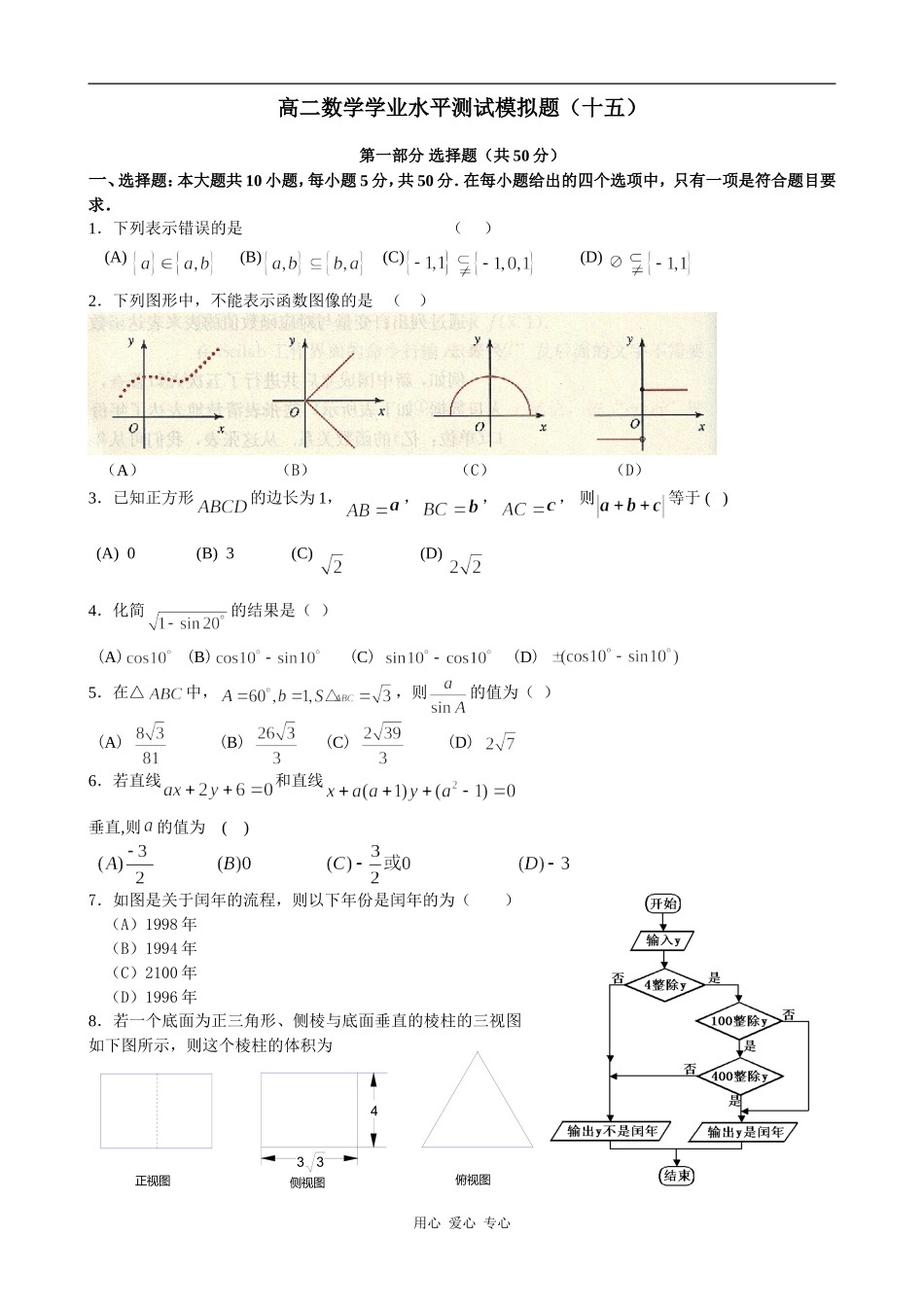
俯视图侧视图正视图334高二数学学业水平测试模拟题(十五)第一部分选择题(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求.1.下列表示错误的是()(A)(B)(C)(D)2.下列图形中,不能表示函数图像的是()(A)(B)(C)(D)3.已知正方形的边长为1,,,,则等于()(A)0(B)3(C)(D)4.化简的结果是()(A)(B)(C)(D)5.在△中,,则的值为()(A)(B)(C)(D)6.若直线和直线垂直,则的值为()7.如图是关于闰年的流程,则以下年份是闰年的为()(A)1998年(B)1994年(C)2100年(D)1996年8.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为用心爱心专心A.B.C.D.69.已知函数,则等于()(A)(B)(C)(D)10.已知,点,,都在二次函数的图像上,则()(A)(B)(C)(D)第二部分非选择题(共100分)二、填空题:本大题共4小题,每小题5分,共20分.11.观察新生婴儿的体重,其频率分布直方图如下图所示,则新生婴儿体重在(2700,3000)内的频率为________.12.过点(2,1)的直线中,被圆截得的最长弦所在直线的方程是.13.已知点P(x,y)在不等式组表示的区域上运动,则z=x-y的取值范围是.14.观察下面的数阵,容易看出,第行最右边的数是,那么第20行最左边的数是____第20行所有数的和是____.1用心爱心专心2345678910111213141516171819202122232425………………三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分12分)要从甲、乙两名划艇运动员中选拔一名去参加比赛,为此对甲、乙两人在相同的条件下进行了6次测试,测得他们最大速度(m/s)的数据如下:甲:27,38,30,37,35,31;乙:33,29,38,34,28,36.试比较这两名划艇运动员谁更优秀.16.(本小题满分13分)已知函数.(1)求的最小正周期;(2)画出函数在区间上的图象17.(本小题满分13分)如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,是PC的中点.(1)证明平面EDB;(2)求证:平面BDE⊥平面PBC.18.(本小题满分14分)某自来水厂蓄水池中有400吨的水,水厂每小时可向蓄水池注入吨水,同时蓄水池又向居民小区供水,小时内,水量为吨().设小时后水池的水量为.(1)写出与的关系式;(2)当时,多少小时后蓄水池的水量最少.19.(本小题满分14分)已知直线有两个不同的交点A,B(1)求m的取值范围;(2)若,求ABC的面积.用心爱心专心ABCDPE20.(本小题满分14分)已知等差数列及等比数列,其中,公比<0,且数列的前三项分别为2、1、4.(Ⅰ)求及;(Ⅱ)求数列的前项和.2007年番禺区高二数学学业水平测试模拟题(十五)参考解答及评分标准一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.题号12345678910答案ABDBCBDBCB二、填空题:本大题主要考查基本知识和基本运算.共4小题,每小题5分,满分20分.第(14)小题的第一个空2分、第二个空3分.(11)解:由直方图的意义可知,各小长方形的面积=组距×=频率,即各小长方形的面积等于相应各组的频率,在区间(2700,3000)内取值的频率为(3000-2700)×0.001=0.3.(12解:圆的最长弦是过圆心的弦,圆心坐标为直线的斜率为3利用直线的点斜式方程即可.(13)[--1,2](14)362,14859三、解答题(15)解:=(27+38+30+37+35+31)=33;=(33+29+38+34+28+36)=33.即两人测试比赛的平均成绩相同.在这种情况下要进一步比较两人成绩的稳定程度.s甲2=[(27-33)2+(38-33)2+(30-33)2+(37-33)2+(35-33)2+(31-33)2]≈15.67;s乙2=[(33-33)2+(29-33)2+(38-33)2+(34-33)2+(28-33)2+(36-33)2]≈12.67.由s乙2