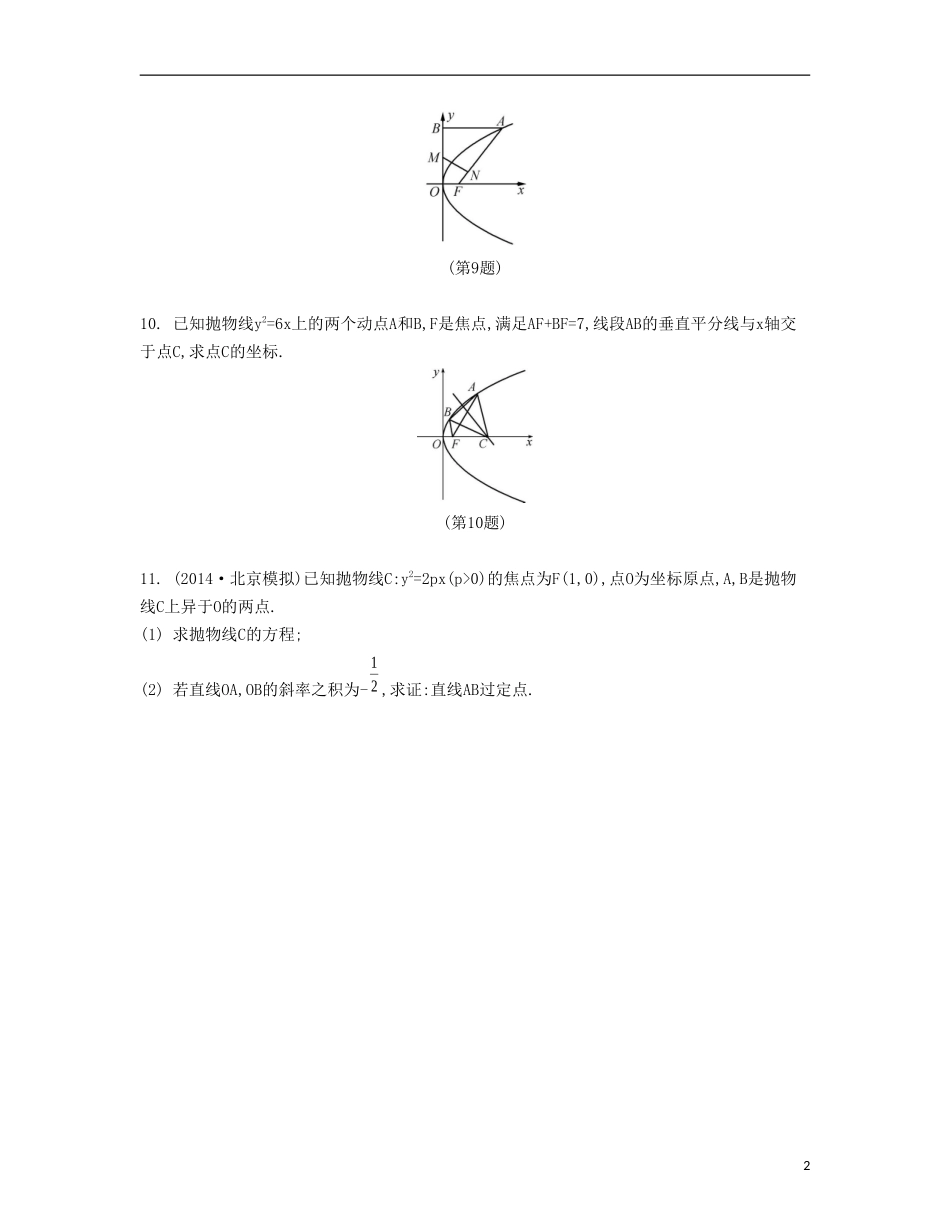
第62课抛物线一、填空题1.已知抛物线C1:x2=2py的焦点在抛物线C2:y=12x2+1上,那么抛物线C1的准线方程为.2.(2014·资阳模拟)已知点P在抛物线x2=4y上,且点P到x轴的距离与点P到此抛物线的焦点的距离之比为1∶3,那么点P到x轴的距离是.3.已知抛物线y2=2px(p>0)上一点Q(4,m)到其焦点的距离为5,则实数m的值为.4.(2014·北京朝阳区模拟)如果点P(2,y0)在以点F为焦点的抛物线y2=4x上,那么PF=.5.(2014·烟台模拟)已知直线l过抛物线y2=4x的焦点F,交抛物线于A,B两点,且点A,B到y轴的距离分别为m,n,那么m+n+2的最小值为.6.已知F为抛物线x2=ay(a>0)的焦点,O为坐标原点,点M为抛物线上的任意一点,过点M作抛物线的切线交x轴于点N.设k1,k2分别为直线MO与直线NF的斜率,则k1k2=.7.(2014·宿州一模)已知抛物线C的顶点在原点,焦点F与双曲线2x3-2y6=1的右焦点重合,过点P(2,0)且斜率为1的直线l与抛物线C交于A,B两点,则弦AB的中点到抛物线准线的距离为.8.(2014·赣州联考)已知过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,O为坐标原点.若AF=3,则△AOB的面积为.二、解答题9.已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点,点A到抛物线准线的距离等于5,过点A作AB垂直于y轴,垂足为B,OB的中点为M.(1)求此抛物线的方程;(2)过点M作MN⊥FA,垂足为N,求点N的坐标.1(第9题)10.已知抛物线y2=6x上的两个动点A和B,F是焦点,满足AF+BF=7,线段AB的垂直平分线与x轴交于点C,求点C的坐标.(第10题)11.(2014·北京模拟)已知抛物线C:y2=2px(p>0)的焦点为F(1,0),点O为坐标原点,A,B是抛物线C上异于O的两点.(1)求抛物线C的方程;(2)若直线OA,OB的斜率之积为-12,求证:直线AB过定点.2第62课抛物线1.y=-1解析:抛物线C1的焦点为F0,2p,所以2p=0+1,p=2,故抛物线C1的方程为x2=4y,其准线方程为y=-1.2.12解析:抛物线的准线为y=-1,设点P到x轴的距离为d,则d+1=3d,解得d=12.3.±4解析:由题意知4+2p=5,解得p=2,所以抛物线的方程为y2=4x.将A(4,m)代入抛物线方程,解得m=±4.4.3解析:根据抛物线的定义知点P到点F的距离等于点P到其准线x=-1的距离,即d=|2-(-1)|=3.5.4解析:由题意知m+n+2=AB,则其最小值即为通径长2p=4.6.-12解析:设M200,xxa,则过点M的抛物线的切线方程为y=02xa(x-x0)+20xa,令y=0,得xN=02x,故N0,02x,F0,4a,则k2=kNF=-02ax.又k1=kMO=0xa,故k1k2=-12.7.11解析:因为双曲线23x-26y=1的右焦点坐标是(3,0),所以2p=3,p=6,即抛物线的标准方程为y2=12x.直线l的方程为y=x-2,设A(x1,y1),B(x2,y2),将y=x-2与y2=12x联立,消去y得x2-16x+4=0,所以x1+x2=16,所以线段AB的中点到抛物线的准线的距离122xxp=1662=11.8.322解析:设直线AB的倾斜角为θ(0<θ<π)及BF=m,因为AF=3,所以点A到准线l:x=-1的距离为3,所以2+3cosθ=3,即cosθ=13,则sinθ=223.因为m=2+mcos(π-θ),所以m=21cos3=32,所以△AOB的面积为S=12×OF×AB×sinθ=12×1×332×223=322.9.(1)因为点A在抛物线y2=2px(p>0)上,点A的横坐标为4,点A到抛物线的准线的距离为5,由抛物线的定义知5=4+2p,所以p=2,故抛物线的方程为y2=4x.(2)由(1)知点A(4,4),B(0,4),所以点M(0,2),而点F(1,0),kAF=43,所以kMN=-34,所以直线MN的方程为3x+4y-8=0,①直线AF的方程为4x-3y-4=0,②联立①②可求得N84,55.10.设A(x1,y1),B(x2,y2),线段AB的中点为M(x0,y0),由AF+BF=7,得132x+232x=7,即x1+x2=4,所以x0=122xx=2,y0=122yy,kAB=2121--yyxx.=212221--66yyyy=216yy=03y,则线段AB的垂直平分线的方程是y-y0=-03y(x-2).①易知x=5,y=0是方程①的一个解,所以线段AB的垂直平分线与x轴的交点C为定点,点C的坐标为(5,0).11.(1)因为焦点为F(1,0),所以p=2,所以抛物线方程为y2=4x.(2)①若直线AB的斜率存在,设其方程为y=kx+b.联立方程组2,4,ykxbyx得k2x2+(2kb-4)x+b2=0.所以x1x2=22bk,y1y2=4bk.4因为直线OA,OB的斜率之积为-12,即11yx·22yx=-12,所以4kb=-12,即b=-8k,代入直线方程,得直线AB的方程为y=kx-8k.所以直线AB过定点(8,0).②若直线AB的斜率不存在,则x1=x2,y1=-y2,由11yx·22yx=-12,可得x1=x2=8,所以直线AB的方程为x=8,过定点(8,0).综上,直线AB过定点.5