高中高二数学1月月考试题04-人教版高二全册数学试题VIP免费

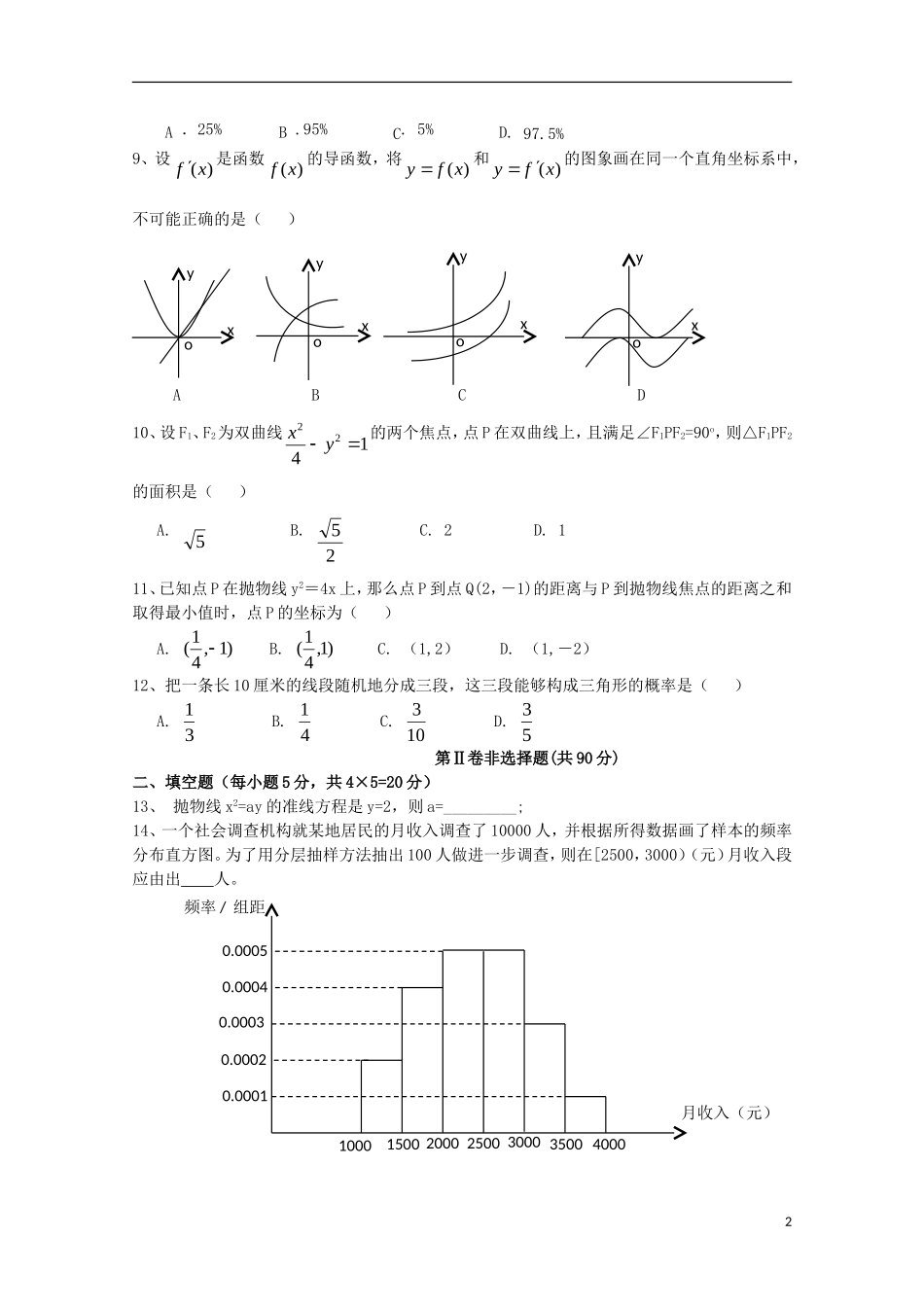
高二数学1月月考试题04第I卷（选择题，共60分）一、选择题（本卷共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个是符合题目要求的.）1、函数f(x)＝x+cosx在点)3(,3f处切线的斜率是（）A.231B.231C.233D.2332、从甲、乙、丙三人中任选两名代表，甲被选中的概率为()A.12B.13C.23D.13、已知椭圆1162522yx上的一点P到椭圆一个焦点的距离为3，则P到另一个焦点的距离为（）A．2B．3C．5D．74、条件210px：，条件2qx：，则p是q的（）.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5、下列命题是真命题的是（）①“若220xy，则,xy不全为零”的否命题；②“正六边形都相似”的逆命题；③“若0m，则20xxm有实根”的逆否命题；④“若123x是有理数，则x是无理数”.A．①④B．③④C．①③④D．①②③④6、已知焦点在x轴上的双曲线，其两条渐近线方程为xy21，则该双曲线的离心率为（）A.5B.45C.5D.257、某射手一次射击中，击中10环、9环、8环的概率分别是0.24,0.28,0.19，则这射手在一次射击中不够9环的概率是（）A.0.48B.0.52C.0.71D.0.298、利用独立性检验来考虑两个分类变量X与Y是否有关系时，通过查阅下表来确定“X和Y有关系”的可信度。如果k≈3.852，那么就有把握认为“X和Y有关系”的百分比为（）2pKk0.500.400.250.150.100.050.0250.0100.0050.001k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.831A．25%B.95%C.5%D.97.5%9、设()fx是函数()fx的导函数，将()yfx和()yfx的图象画在同一个直角坐标系中，不可能正确的是（）ABCD10、设F1、F2为双曲线1422yx的两个焦点，点P在双曲线上，且满足∠F1PF2=90o，则△F1PF2的面积是（）A.5B.25C.2D.111、已知点P在抛物线y2＝4x上，那么点P到点Q(2，－1)的距离与P到抛物线焦点的距离之和取得最小值时，点P的坐标为（）A.)1,41(B.)1,41(C.（1,2）D.（1,－2）12、把一条长10厘米的线段随机地分成三段，这三段能够构成三角形的概率是（）A.31B.41C.103D.53第Ⅱ卷非选择题(共90分)二、填空题（每小题5分，共4×5=20分）13、抛物线x2=ay的准线方程是y=2，则a=_________;14、一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图。为了用分层抽样方法抽出100人做进一步调查，则在[2500，3000）（元）月收入段应由出人。21000150020002500300035004000月收入（元）0.00010.00020.00030.00040.0005频率/组距xyoxyoxyoxyo15、已知x与y之间的一组数据为x0123y135-a7+a则y与x的回归直线方程abxy必过定点______;16、函数f(x)=2x2－lnx的单调递减区间是_______;三、解答题：（共6个小题，共70分，要求写出文字说明、证明过程或演算步骤）17、（10分）已知椭圆的中心在原点，离心率21e，且它的一个焦点与抛物线xy42的焦点重合，求此椭圆方程。18、（12分）已知命题p：“方程x2+mx+1=0有两个相异负根”,命题q：“方程4x2+4(m－2)x+1=0无实根”，若p或q为真，p且q为假，试求实数m的取值范围。19、（12分）某初级中学共有学生2000名，各年级男、女生人数如下表：初一年级初二年级初三年级女生373xy男生377370z已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19。（1）求x的值；（2）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？（3）已知y245,z245,求初三年级中女生比男生多的概率。7.（12分）已知函数f(x)＝x3＋3ax2＋3bx＋c在x＝2处有极值，其图像在x＝1处的切线与直线6x＋2y＋5＝0平行。3二、.求a、b的值；三、.当x∈[1,3]时，f(x)＞1－4c2恒成立，求实数c的取值范围。21、（12分）已知椭圆14922yx内有一点P（2，1）,过点P作直线交椭圆于A、B两点。(1).若弦AB恰好被点P平分，求直线AB的方程；(2).当原点O到直线AB的距离取最大值时，求△AOB的面积。22、（12分）已知函数f(x)＝x3－x＋a，x∈R.(2).求f(x)的单调区间；(2).若曲线y＝f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，求a的取值参考答案一、选择题（每小题5分，...