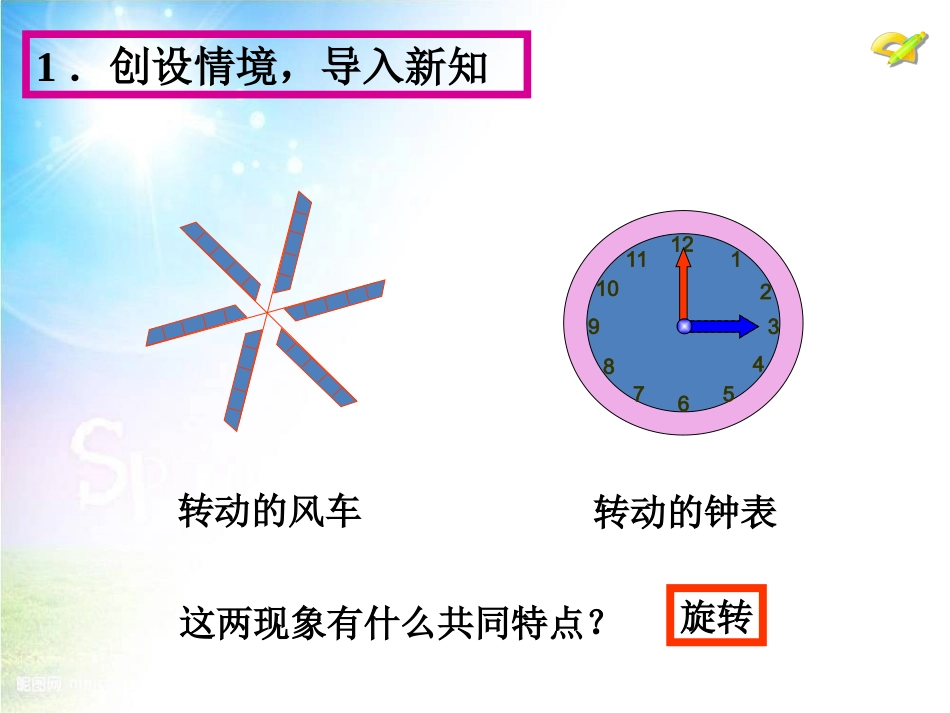
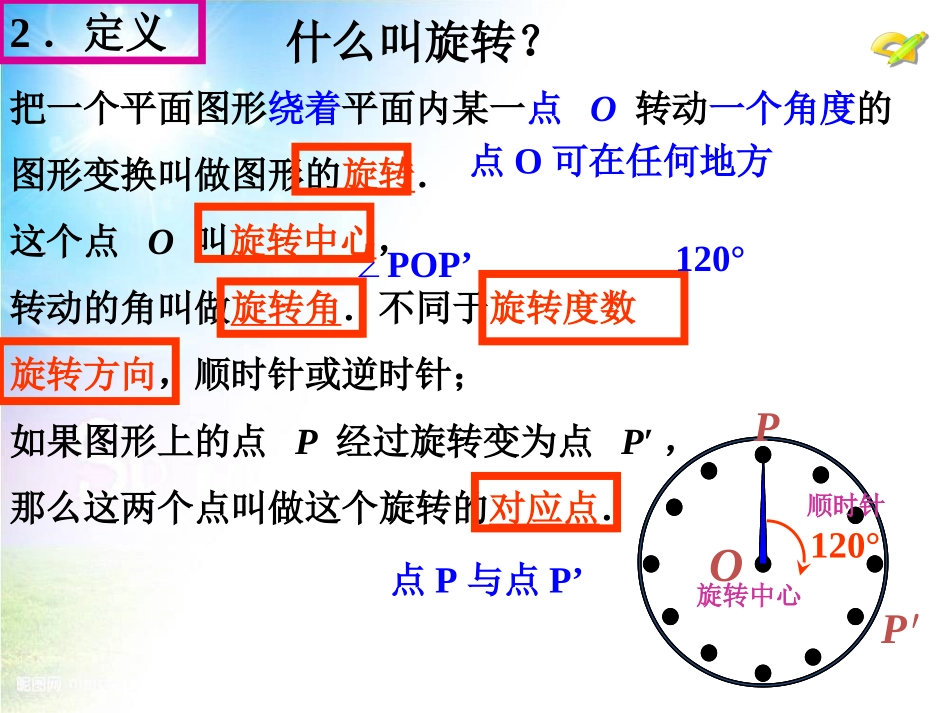
23.1图形的旋转(第1课时)九年级上册1.创设情境,导入新知126123457891011转动的风车转动的钟表这两现象有什么共同特点?旋转OP′P2.定义120°把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.不同于旋转度数旋转方向,顺时针或逆时针;如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.∠POP’120°点P与点P’旋转中心顺时针什么叫旋转?点O可在任何地方1.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?练习12612345789101190°360°12=30°归纳:1、钟表中,每两个数字之间,即每格的度数是30°2、分针1小时转360°,n分钟转3、时针1小时转30°,n分钟转360°×n60=6n30°×n60=n22.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?3.小试牛刀旋转中心O旋转角3.探究把△ABC旋转到△A’B’C’观察思考,右图中有哪些相等的线段和相等的角?答:相等的线段:AB=A’B’AC=A’C’BC=B’C’OA=OA’OB=OB’OC=OC’对应边相等对应点与旋转中心的连线相等相等的角:∠A=∠A’∠B=∠B’∠C=∠C’对应角相等∠AOA’=∠BOB’=COC’=∠旋转度数旋转度数△ABCA’B’C’≌△4.旋转的三要素美丽的图案是这样形成的.1.旋转中心2.旋转角度3.旋转方向思考:相同的图形,为什么会旋转出不同的图案?旋转角度不同旋转中心不同旋转中心不同旋转角度不同ABCB′C′A′O5.作旋转图(无网格时)求作:△ABC绕点O,顺时针旋转90°得到的△A′B′C′∴△A′B′C′即为所求归纳:作图步骤(无网格)1、连结对应点与中心2、按旋转方向,角度,画出旋转后的对应线3、截取对应点4、重复步骤1~3,以确定每一个对应点5、连结各对应点6、写结论:“∴…即为所求”xO-4-3-2-11234-12341-2-3ABCA’B’C’作图:把△ABC绕点O顺时针旋转90°,请画出旋转后的图形。5.作旋转图(有网格时)ABO5.应用1下图为4×4的正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°,你能画出△OAB旋转后的图形△OAB吗?'''A'B'2如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,你能画出旋转后的图形吗?试一试你有几种方法?7.应用ABCED方法1:F图中△ABF为所求图形.7.应用ABCED方法2:F图中△ABF为所求图形.7.应用ABCED方法3:F图中△ABF为所求图形.7.应用ABCED小结1、相关概念旋转、旋转中心、旋转角、旋转度数、旋转方向、对应边、对应角,2、旋转的性质对应点与旋转中心的连线相等;每一对对应点与旋转中心所连线段的夹角等于旋转角;对应边相等、对应角相等,旋转前后的图形全等。3、旋转的三要素旋转中心、旋转度数、旋转方向、4、旋转作图:用直尺、圆规、量角器等工具