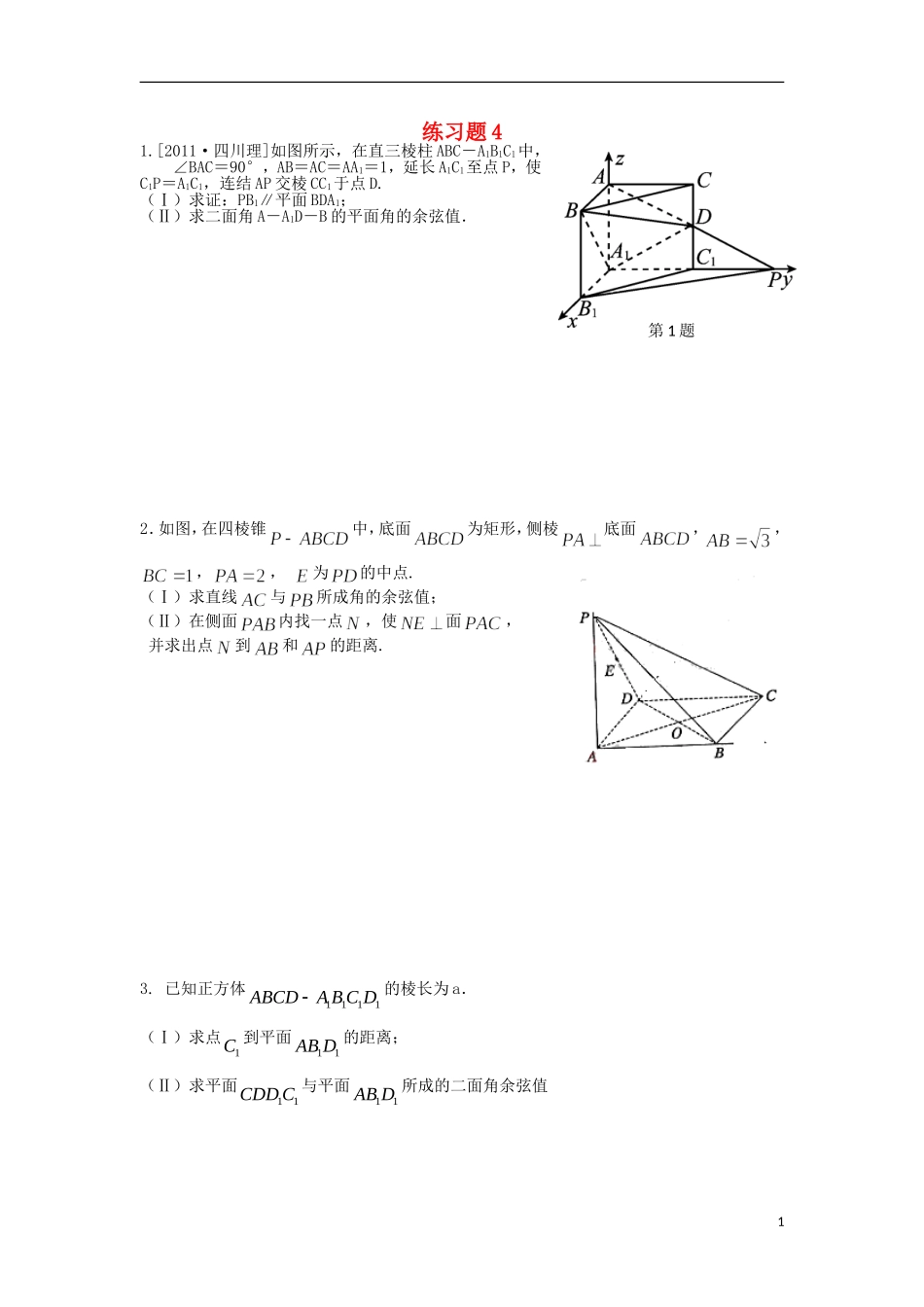
练习题41.[2011·四川理]如图所示,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.(Ⅰ)求证:PB1∥平面BDA1;(Ⅱ)求二面角A-A1D-B的平面角的余弦值.2.如图,在四棱锥中,底面为矩形,侧棱底面,,,,为的中点.(Ⅰ)求直线与所成角的余弦值;(Ⅱ)在侧面内找一点,使面,并求出点到和的距离.3.已知正方体1111ABCDABCD的棱长为a.(Ⅰ)求点1C到平面11ABD的距离;(Ⅱ)求平面11CDDC与平面11ABD所成的二面角余弦值1第1题4.已知四棱锥的底面为直角梯形,,底面,且,,是的中点。(Ⅰ)证明:面面;(Ⅱ)求与所成的角;(Ⅲ)求面与面所成二面角的余弦值。5.如图,PA平面ABCD,四边形ABCD是正方形,2ADPA,点E、F、G分别为线段PA、PD和CD的中点.(Ⅰ)求异面直线EG与BD所成角的余弦值(Ⅱ)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离恰为45?若存在,求出线段CQ的长;若不存在,请说明理由.2第4题GFECPADBQ第5题6.如图,在四棱锥中,底面为矩形,底面,是上一点,.已知求:(Ⅰ)异面直线与的距离;(Ⅱ)二面角的大小.3