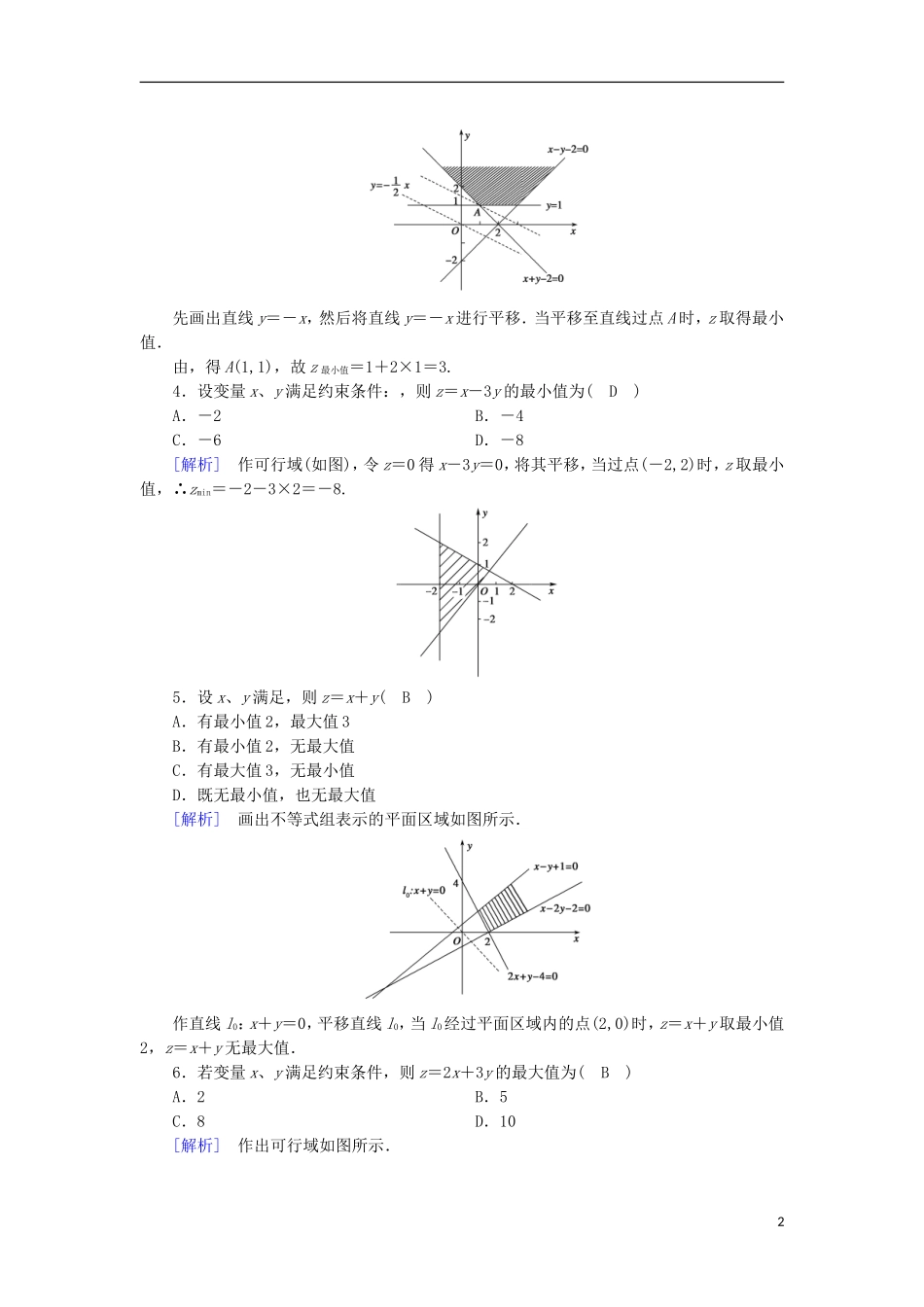
2017春高中数学第3章不等式3.5二元一次不等式(组)与简单的线性规划问题第2课时简单的线性规划的概念课时作业新人教B版必修5基础巩固一、选择题1.(2015·天津理,2)设变量x、y满足约束条件,则目标函数z=x+6y的最大值为(C)A.3B.4C.18D.40[解析]不等式,所表示的平面区域如下图所示,当z=x+6y所表示直线经过点B(0,3)时,z有最大值18.故选C.2.(2015·北京理,2)若x、y满足,则z=x+2y的最大值为(D)A.0B.1C.D.2[解析]如图,先画出可行域,由于z=x+2y,则y=-x+z,令z=0,作直线y=-x,在可行域中作平行线,得最优解(0,1),此时直线的截距最大,z取得最大值2.故选D.3.设变量x、y满足约束条件,则目标函数z=x+2y的最小值为(B)A.2B.3C.4D.5[解析]根据约束条件作出可行域,如图阴影部分所示.由z=x+2y得y=x+.1先画出直线y=-x,然后将直线y=-x进行平移.当平移至直线过点A时,z取得最小值.由,得A(1,1),故z最小值=1+2×1=3.4.设变量x、y满足约束条件:,则z=x-3y的最小值为(D)A.-2B.-4C.-6D.-8[解析]作可行域(如图),令z=0得x-3y=0,将其平移,当过点(-2,2)时,z取最小值,∴zmin=-2-3×2=-8.5.设x、y满足,则z=x+y(B)A.有最小值2,最大值3B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值[解析]画出不等式组表示的平面区域如图所示.作直线l0:x+y=0,平移直线l0,当l0经过平面区域内的点(2,0)时,z=x+y取最小值2,z=x+y无最大值.6.若变量x、y满足约束条件,则z=2x+3y的最大值为(B)A.2B.5C.8D.10[解析]作出可行域如图所示.2作直线l0:2x+3y=0,再作一组平行于l0的直线l:2x+3y=z,当直线l经过点A时,z=2x+3y取得最大值.由,得,所以点A的坐标为(4,-1),所以zmax=2×4+3×(-1)=5.故选B.二、填空题7.若变量x、y满足约束条件,则z=3x+y的最小值为1.[解析]由题意,作出约束条件组成的可行域如图所示,当目标函数z=3x+y,即y=-3x+z过点(0,1)时z取最小值为1.8.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则|OM|的最小值是.[解析]本题考查不等式组表示平面区域及点到直线距离问题.不等式组所表示平面区域如图,|OM|最小即O到直线x+y-2=0的距离.故|OM|的最小值为=.三、解答题9.在平面直角坐标系中,不等式组(a为正常数)表示的平面区域的面积是4,求2x+y的最大值.[解析]由题意得:3S=×2a×a=4,∴a=2.设z=2x+y,∴y=-2x+z,由,得(2,2),即z在(2,2)处取得最大值6.能力提升一、选择题1.(2015·安徽文,5)已知x、y满足约束条件,则z=-2x+y的最大值是(A)A.-1B.-2C.-5D.1[解析]根据题意作出约束条件确定的可行域,如图.令z=-2x+y,则y=2x+z,可知在图中A(1,1)处,z=-2x+y取到最大值-1,故选A.2.已知点P(x,y)的坐标满足条件,那么x2+y2的取值范围是(D)A.[1,4]B.[1,5]C.[,4]D.[,5][解析]不等式组所表示的平面区域,如图中的阴影部分,显然,原点O到直线2x+y-2=0的距离最小,为=,此时可得(x2+y2)min=;点(1,2)到原点O的距离最大,为=,此时可得(x2+y2)max=5.故选D.3.点P(2,t)在不等式组表示的平面区域内,则点P(2,t)到直线3x+4y+10=0距离的最大值为(B)A.2B.4C.6D.8[解析]画出不等式组表示的平面区域(如下图中阴影部分所示).结合图形可知,点P在直线x+y-3=0上时,P点到直线3x+4y+10=0的距离最大.由得P点坐标为(2,1),故所求最大距离为dmax==4.44.(2015·湖南文,4)若变量x、y满足约束条件,则z=2x-y的最小值为(A)A.-1B.0C.1D.2[解析]由约束条件作出可行域,然后根据所得图得到最优解,求出最优解的坐标,数形结合得到答案.由约束条件,作出可行域如图,由图可知,最优解为A,联立,∴.∴A(0,1),∴z=2x-y在点A处取得最小值为2×0-1=-1,故选A.二、填空题5.在△ABC中,三个顶点分别为A(2,4)、B(-1,2)、C(1,0),点P(x,y)在△ABC的内部及其边界上运动,则y-x的取值范围为[-1,3].[解析]画出三角形区域如图,易知kAB=<1,令z=y-x,则y=x+z,作出直...