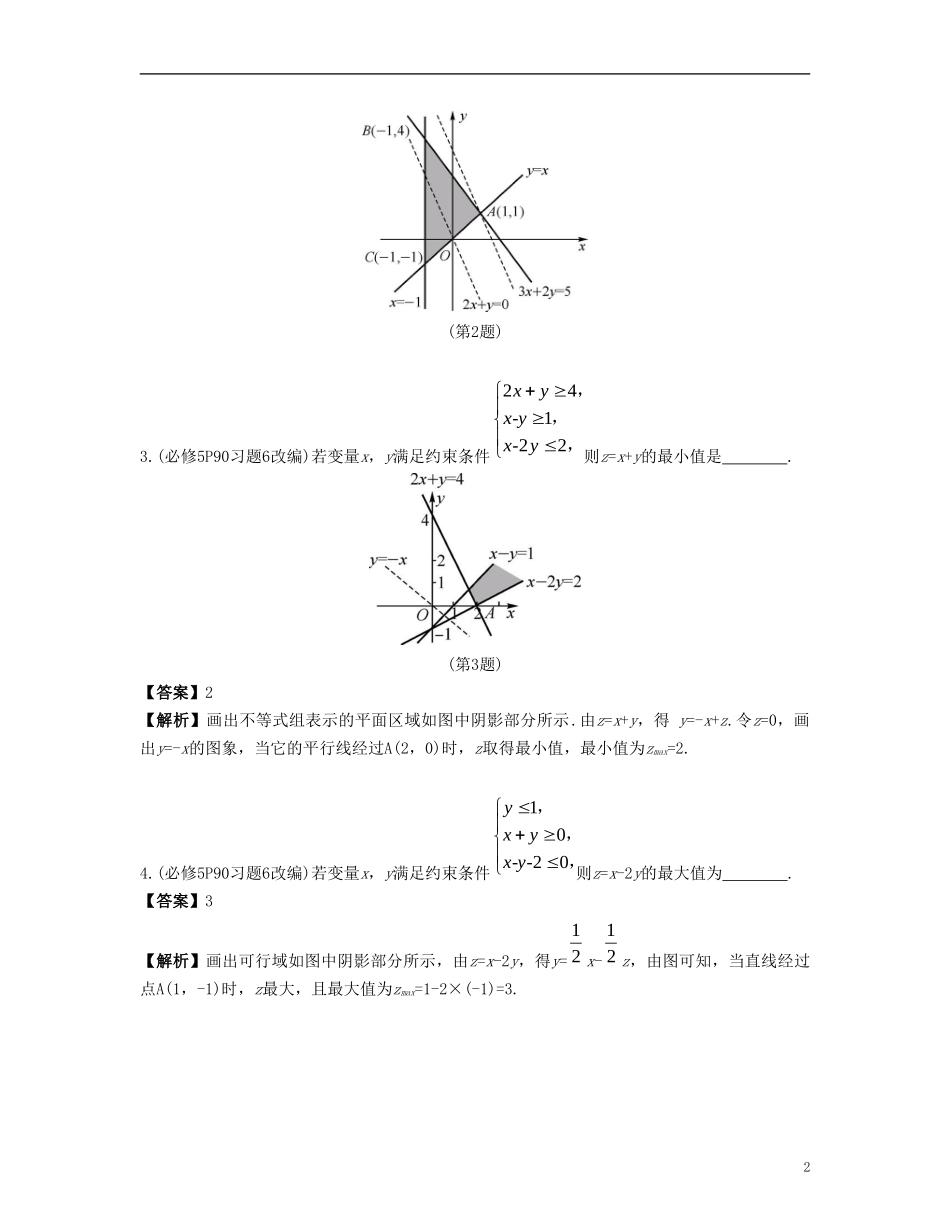
第46课简单的线性规划(本课时对应学生用书第页)自主学习回归教材1.(必修5P95习题11改编)若实数x,y满足不等式组1-102--20xxyxy,,,则z=x2+y2的最小值是.(第1题)【答案】5【解析】作出可行域如图中阴影部分所示,z=x2+y2的最小值表示阴影部分(包含边界)中的点到原点的距离的最小值的平方,由图可知直线x-y+1=0与直线x=1的交点(1,2)到原点的距离最近,故z=x2+y2的最小值为12+22=5.2.(必修5P94习题8改编)若变量x,y满足约束条件-1325xyxxy,,,则z=2x+y的最大值为.【答案】3【解析】作出可行域如图中阴影部分所示,可得直线y=x与直线3x+2y=5的交点A(1,1)为最优解点,所以当x=1,y=1时,zmax=3.1(第2题)3.(必修5P90习题6改编)若变量x,y满足约束条件24-1-22xyxyxy,,,则z=x+y的最小值是.(第3题)【答案】2【解析】画出不等式组表示的平面区域如图中阴影部分所示.由z=x+y,得y=-x+z.令z=0,画出y=-x的图象,当它的平行线经过A(2,0)时,z取得最小值,最小值为zmax=2.4.(必修5P90习题6改编)若变量x,y满足约束条件10--20yxyxy,,,则z=x-2y的最大值为.【答案】3【解析】画出可行域如图中阴影部分所示,由z=x-2y,得y=12x-12z,由图可知,当直线经过点A(1,-1)时,z最大,且最大值为zmax=1-2×(-1)=3.2(第4题)1.线性规划及其相关概念(1)目标函数:欲达到最大值或最小值所涉及的变量x,y的解析式称为目标函数.关于x,y的一次目标函数称为线性目标函数.(2)约束条件:由x,y的不等式(或方程)组成的不等式组称为x,y的约束条件.关于x,y的一次不等式或方程组成的不等式组称为x,y的线性约束条件.(3)可行解:满足线性约束条件的解(x,y)称为可行解.(4)可行域:所有可行解组成的集合称为可行域.(5)最优解:使目标函数取得最大值或最小值的可行解称为最优解.(6)求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题.2.解线性规划问题的步骤(1)画,即画出线性约束条件所表示的可行域;(2)移,即在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;(3)求,即通过解方程组求最优解;(4)答,即给出答案.【要点导学】要点导学各个击破3简单的线性规划问题例1(2015·天津卷)设变量x,y满足约束条件-20-202-80xxyxy,,,则目标函数z=3x+y的最大值为.【思维引导】先根据约束条件画出可行域,将z=3x+y转化成直线y=-3x+z,得到z的几何意义是纵截距.通过平移直线来求出z的最大值.(例1)【答案】9【解析】方法一:作出约束条件表示的平面区域如图中的阴影部分所示,根据目标函数的几何意义可知,目标函数在点A(2,3)处取得最大值,且zmax=9.方法二:z=3x+y=52(x-2)+12(x+2y-8)+9≤9,当x=2,y=3时取得最大值.【精要点评】(1)线性规划是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值.(2)解决此类问题常利用数形结合,根据约束条件画可行域时,准确作出图形是解决问题的关键.(3)要弄清与z有关的量的几何意义.常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离.(4)在直线平移过程中要注意目标直线的斜率与可行域中各直线斜率的比较.变式(2015·全国卷)若变量x,y满足约束条件-20-2102-20xyxyxy,,,则z=3x+y的最大值为.4(变式)【答案】4【解析】作出约束条件表示的可行域如图中阴影部分所示,当目标函数线平移至经过可行域的顶点A(1,1)时,目标函数z取得最大值,故zmax=3×1+1=4.非线性目标函数的最值问题例2已知变量x,y满足约束条件-4-335251xyxyx,,,试求解下列问题.(1)z=22xy的最大值和最小值;(2)z=2yx的最大值和最小值;(3)z=|3x+4y+3|的最大值和最小值.【思维引导】(1)z的几何意义是区域中的点(x,y)到原点(0,0)的距离;(2)z的几何意义是指区域中的点(x,y)与点(-2,0)连线的斜率;(3)5z的几何意义是表示区域中的点(x,y)到直线3x+4y+3=0的距离.(例2)5【解答】作出约束条件表示的可行域如图中阴影部分所示,易得A(1,1),B(5,...