（江苏专用）高考数学大一轮复习 第十一章 第62课 抛物线自主学习-人教版高三全册数学试题VIP免费

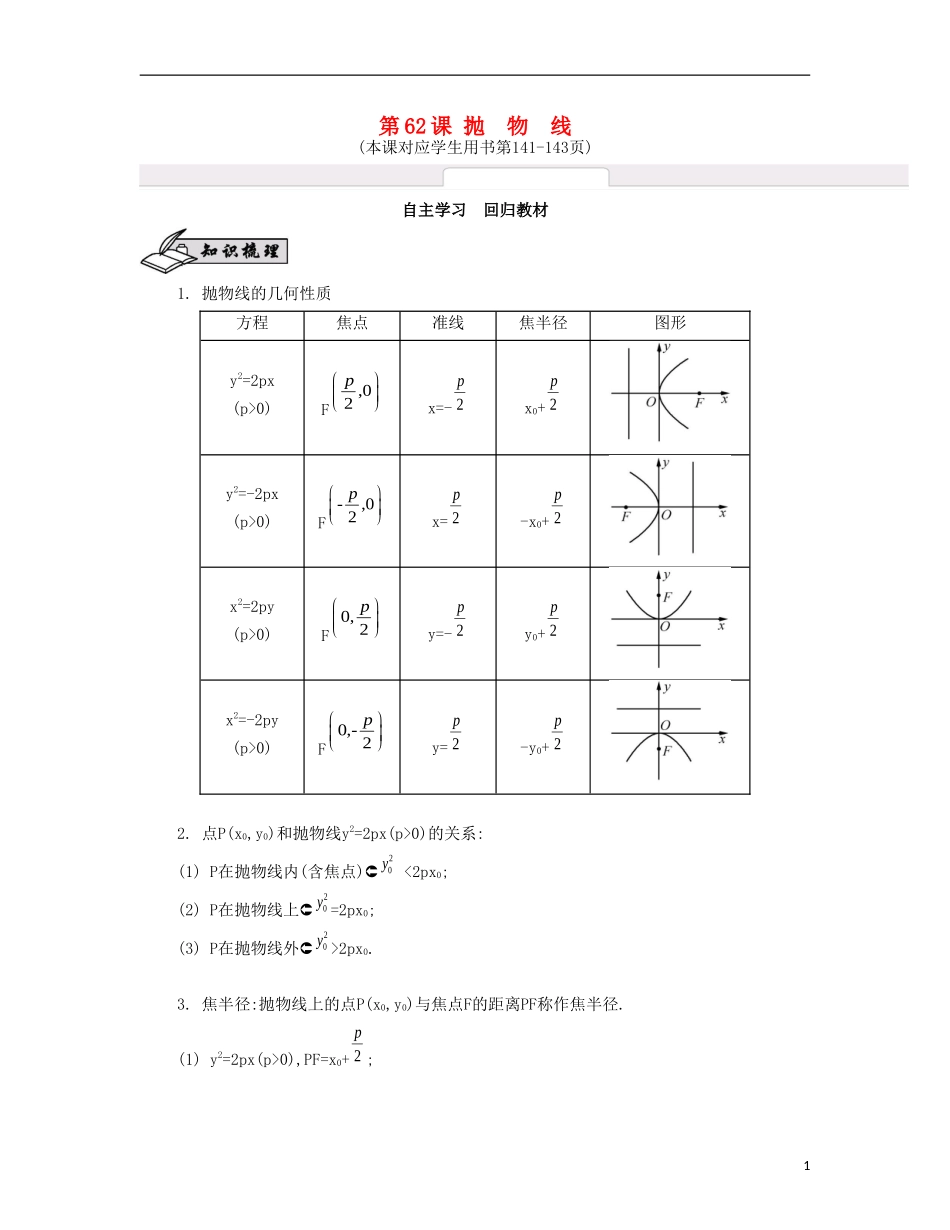
第62课抛物线(本课对应学生用书第141-143页)自主学习回归教材1.抛物线的几何性质方程焦点准线焦半径图形y2=2px(p>0)F,02px=-2px0+2py2=-2px(p>0)F-,02px=2p-x0+2px2=2py(p>0)F0,2py=-2py0+2px2=-2py(p>0)F0,-2py=2p-y0+2p2.点P(x0,y0)和抛物线y2=2px(p>0)的关系:(1)P在抛物线内(含焦点)20y<2px0;(2)P在抛物线上20y=2px0;(3)P在抛物线外20y>2px0.3.焦半径:抛物线上的点P(x0,y0)与焦点F的距离PF称作焦半径.(1)y2=2px(p>0),PF=x0+2p;1(2)y2=-2px(p>0),PF=-x0+2p;(3)x2=2py(p>0),PF=y0+2p;(4)x2=-2py(p>0),PF=-y0+2p.4.焦点弦:AB为抛物线y2=2px(p>0)经过焦点F的弦(简称焦点弦).已知点A(x1,y1),B(x2,y2),直线AB的倾斜角为α,那么:(1)x1x2=24p;(2)y1y2=-p2;(3)AB=x1+x2+p=22ipsn,当且仅当α=2时,ABmin=2p.1.(选修2-1P46例1改编)若抛物线的准线方程为x=1,则该抛物线的焦点坐标为.[答案](-1,0)[解析]因为抛物线的准线与x轴的交点和焦点关于y轴对称,所以焦点坐标为(-1,0).2.(选修2-1P47习题2改编)抛物线y2=ax的准线方程为.[答案]x=-4a3.(选修2-1P48习题5改编)顶点在原点、对称轴为坐标轴、焦点在直线2x-y+4=0上的抛物线的标准方程为.[答案]x2=16y或y2=-8x4.(选修1-1P47练习3改编)已知一个抛物线形拱桥,当水面离拱顶2m时,水面宽4m.若水面上升1m,则水面宽度为m.(第4题)2[答案]22[解析]以抛物线顶点为原点、过焦点且垂直于抛物线准线的直线为y轴建立如图所示的平面直角坐标系,设抛物线方程为x2=-2py,则M(2,-2)是抛物线上的点,所以2p=2,抛物线方程是x2=-2y,若水面上升1m,则点N(m,-1)在抛物线上,所以m=±2,所以水面宽度是22m.5.(选修1-1P41练习2改编)若P(x0,4)是抛物线y2=-32x上一点,F是抛物线的焦点,则PF=.[答案]172[解析]因为点P(x0,4)在抛物线y2=-32x上,所以x0=-12,抛物线的准线是x=8,所以PF=8-x0=172.3