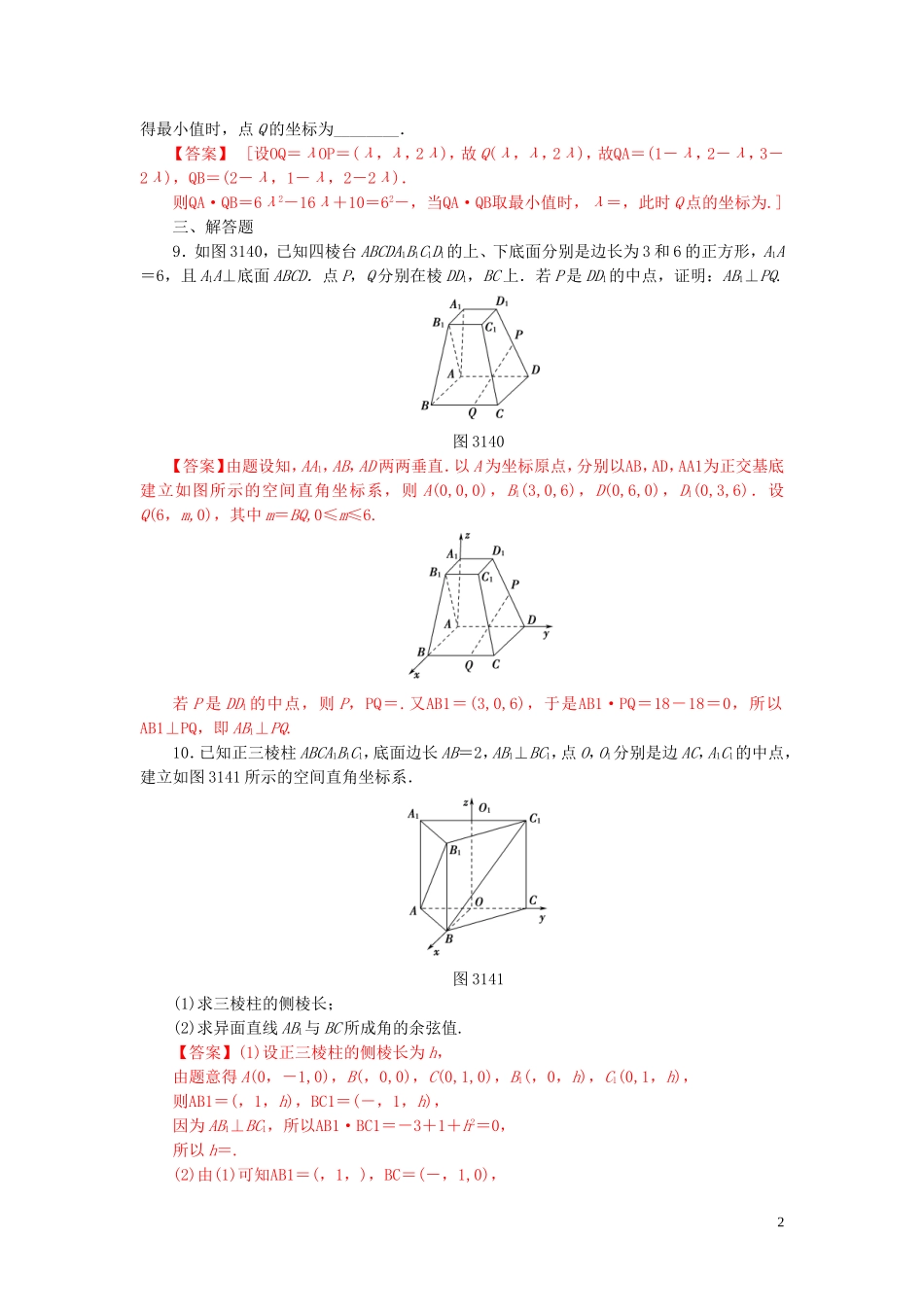
3.1.5空间向量运算的坐标表示(建议用时:40分钟)一、选择题1.已知a=(1,-2,1),a-b=(-1,2,-1),则b=()A.(2,-4,2)B.(-2,4,-2)C.(-2,0,-2)D.(2,1,-3)【答案】A[b=a-(a-b)=(1,-2,1)-(-1,2,-1)=(2,-4,2).]2.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离|CM|的值为()A.B.C.D.【答案】C[ AB的中点M,∴CM=,故|CM|=|CM|==.]3.已知a=(x,1,2),b=(1,2,-y),且(2a+b)∥(-a+2b),则()A.x=,y=1B.x=,y=-4C.x=2,y=-D.x=1,y=-1【答案】B[2a+b=(2x+1,4,4-y),-a+2b=(2-x,3,-2y-2), (2a+b)∥(-a+2b),则存在非零实数λ,使得2a+b=λ(-a+2b),∴∴.]4.已知向量a=(-2,x,2),b=(2,1,2),c=(4,-2,1),若a⊥(b-c),则x的值为()A.-2B.2C.3D.-3【答案】A[ b-c=(-2,3,1),a·(b-c)=4+3x+2=0,∴x=-2.]5.已知a+b=(2,,2),a-b=(0,,0),则cos〈a,b〉=()A.B.C.D.【答案】C[由已知,得a=(1,,),b=(1,0,),∴cos〈a,b〉===.]二、填空题6.已知a=(1,1,0),b=(0,1,1),c=(1,0,1),p=a-b,q=a+2b-c,则p·q=________.【答案】-1[ p=a-b=(1,0,-1),q=a+2b-c=(0,3,1),∴p·q=1×0+0×3+(-1)×1=-1.]7.已知a=(cosα,1,sinα),b=(sinα,1,cosα),则向量a+b与a-b的夹角是________.【答案】90°[a+b=(cosα+sinα,2,sinα+cosα),a-b=(cosα-sinα,0,sinα-cosα),∴(a+b)·(a-b)=0,∴(a+b)⊥(a-b).]8.已知点A(1,2,3),B(2,1,2),P(1,1,2),O(0,0,0),点Q在直线OP上运动,当QA·QB取基础篇1得最小值时,点Q的坐标为________.【答案】[设OQ=λOP=(λ,λ,2λ),故Q(λ,λ,2λ),故QA=(1-λ,2-λ,3-2λ),QB=(2-λ,1-λ,2-2λ).则QA·QB=6λ2-16λ+10=62-,当QA·QB取最小值时,λ=,此时Q点的坐标为.]三、解答题9.如图3140,已知四棱台ABCDA1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD.点P,Q分别在棱DD1,BC上.若P是DD1的中点,证明:AB1⊥PQ.图3140【答案】由题设知,AA1,AB,AD两两垂直.以A为坐标原点,分别以AB,AD,AA1为正交基底建立如图所示的空间直角坐标系,则A(0,0,0),B1(3,0,6),D(0,6,0),D1(0,3,6).设Q(6,m,0),其中m=BQ,0≤m≤6.若P是DD1的中点,则P,PQ=.又AB1=(3,0,6),于是AB1·PQ=18-18=0,所以AB1⊥PQ,即AB1⊥PQ.10.已知正三棱柱ABCA1B1C1,底面边长AB=2,AB1⊥BC1,点O,O1分别是边AC,A1C1的中点,建立如图3141所示的空间直角坐标系.图3141(1)求三棱柱的侧棱长;(2)求异面直线AB1与BC所成角的余弦值.【答案】(1)设正三棱柱的侧棱长为h,由题意得A(0,-1,0),B(,0,0),C(0,1,0),B1(,0,h),C1(0,1,h),则AB1=(,1,h),BC1=(-,1,h),因为AB1⊥BC1,所以AB1·BC1=-3+1+h2=0,所以h=.(2)由(1)可知AB1=(,1,),BC=(-,1,0),2所以AB1·BC=-3+1=-2.因为|AB1|=,|BC|=2,所以cos〈AB1,BC〉==-.所以异面直线AB1与BC所成角的余弦值为.1.已知A(1,2,-1),B(5,6,7),则直线AB与平面xOz交点的坐标是()A.(0,1,1)B.(0,1,-3)C.(-1,0,3)D.(-1,0,-5)【答案】D[设直线AB与平面xOz交点的坐标是M(x,0,z),则AM=(x-1,-2,z+1).又AB=(4,4,8),AM与AB共线,∴AM=λAB,即,解得x=-1,z=-5,∴点M的坐标为(-1,0,-5).故选D.]2.直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为()A.B.C.D.【答案】C[建立如图所示的空间直角坐标系Cxyz,设BC=2,则B(0,2,0),A(2,0,0),M(1,1,2),N(1,0,2),所以BM=(1,-1,2),AN=(-1,0,2),故BM与AN所成角θ的余弦值cosθ===.]3.如图3142,在三棱锥VABC中,顶点C在空间直角坐标系的原点处,顶点A,B,V分别在x,y,z轴上,D是线段AB的中点,且AC=BC=2,当∠VDC=60°时,异面直线AC与VD所成角的余弦值为________.图3142【答案】[由题意,A(2,0,0),...