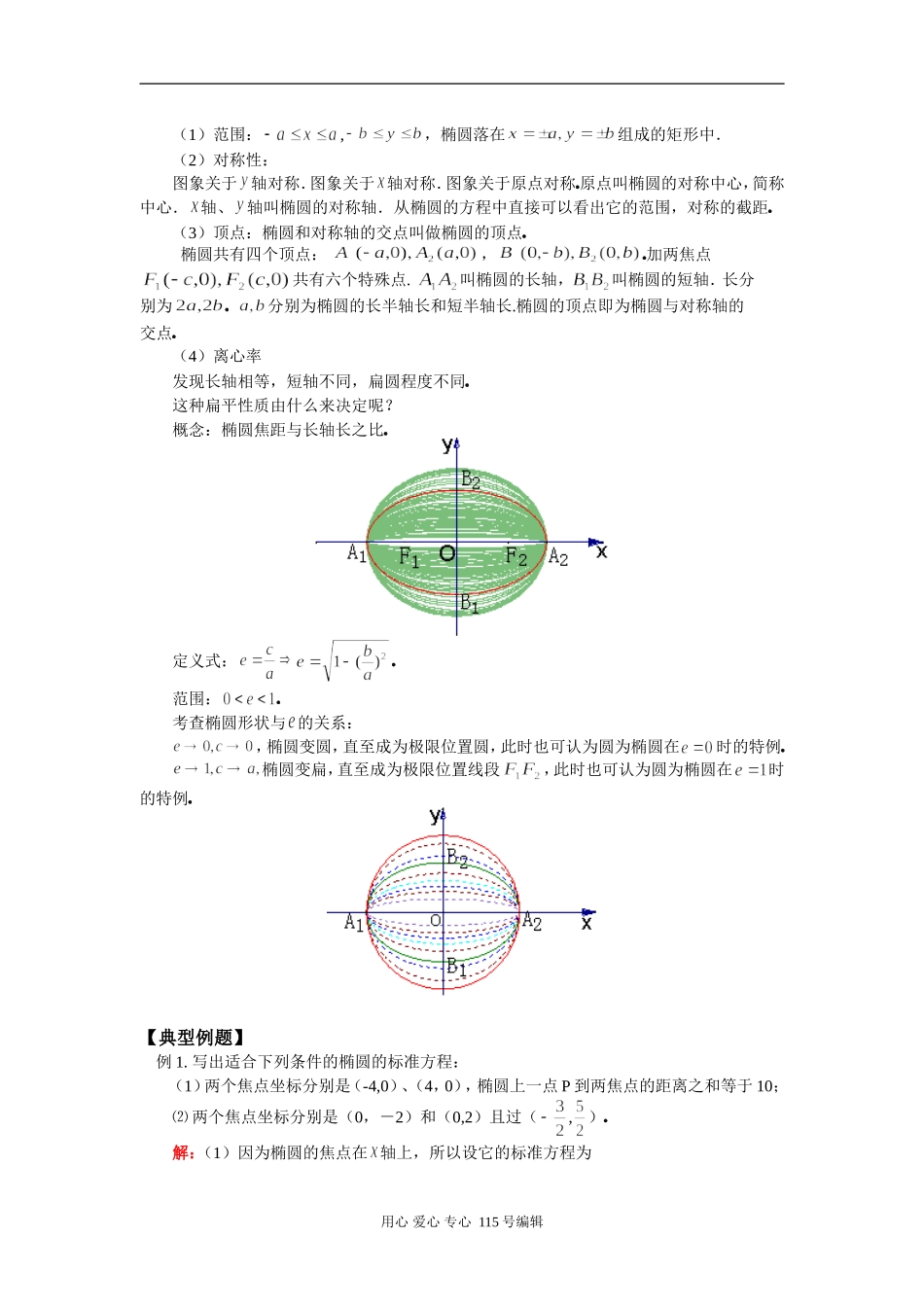
高二数学常用逻辑用语、圆锥曲线与方程苏教版【本讲教育信息】一.教学内容:常用逻辑用语、圆锥曲线与方程二、本周教学目标:1.理解四种命题的关系,并能利用这个关系判断命题的真假奎屯王新敞新疆2.正确理解充分条件、必要条件和充要条件三个概念,并能在判断、论证中正确运用3.能正确运用椭圆的定义与标准方程解题,学会用待定系数法与定义法求椭圆的方程奎屯王新敞新疆三、本周知识要点:(一)常用逻辑用语1.命题及其相互关系(1)四种命题及其形式原命题:若p则q;逆命题:若q则p;否命题:若p则q;逆否命题:若q则p互逆命题、互否命题与互为逆否命题都是说两个命题的关系,若把其中一个命题叫做原命题时,另一个命题就叫做原命题的逆命题、否命题与逆否命题。因此,四种命题之间的相互关系,可用下图表示:(2)四种命题的真假关系一个命题的真假与其他三个命题的真假有如下三条关系:①原命题为真,它的逆命题不一定为真奎屯王新敞新疆②原命题为真,它的否命题不一定为真奎屯王新敞新疆③原命题为真,它的逆否命题一定为真奎屯王新敞新疆2.充分条件与必要条件若pq,则说p是q的充分条件,q是p的必要条件.若pq,但pq,则说p是q的充分而不必要条件;若pq,但pq,则说p是q的必要而不充分条件;若pq,且pq,则说p是q的既不充分也不必要条件.例如,“x>2”是“x>1”的充分而不必要的条件;“x>1”是“x>2”的必要而不充分的条件;“x>0,y>0”是“x+y<0”的既不充分也不必要的条件.3.简单的逻辑联结词(1)“且”、“或”、“非”用心爱心专心115号编辑(2)量词“”的否定为“”“”的否定为“”(二)圆锥曲线1.椭圆定义:平面内与两个定点的距离之和等于常数(大于)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距奎屯王新敞新疆2.椭圆标准方程:(1).(a>b>0)它所表示的椭圆的焦点在轴上,焦点是,中心在坐标原点的椭圆方程.其中奎屯王新敞新疆(2).(a>b>0)它所表示的椭圆的焦点在轴上,焦点是,中心在坐标原点的椭圆方程奎屯王新敞新疆其中奎屯王新敞新疆3.椭圆的性质:由椭圆方程用心爱心专心115号编辑(1)范围:,,椭圆落在组成的矩形中.(2)对称性:图象关于轴对称.图象关于轴对称.图象关于原点对称奎屯王新敞新疆原点叫椭圆的对称中心,简称中心.轴、轴叫椭圆的对称轴.从椭圆的方程中直接可以看出它的范围,对称的截距奎屯王新敞新疆(3)顶点:椭圆和对称轴的交点叫做椭圆的顶点奎屯王新敞新疆椭圆共有四个顶点:,奎屯王新敞新疆加两焦点共有六个特殊点.叫椭圆的长轴,叫椭圆的短轴.长分别为奎屯王新敞新疆分别为椭圆的长半轴长和短半轴长.椭圆的顶点即为椭圆与对称轴的交点奎屯王新敞新疆(4)离心率发现长轴相等,短轴不同,扁圆程度不同奎屯王新敞新疆这种扁平性质由什么来决定呢?概念:椭圆焦距与长轴长之比奎屯王新敞新疆定义式:奎屯王新敞新疆范围:奎屯王新敞新疆考查椭圆形状与的关系:,椭圆变圆,直至成为极限位置圆,此时也可认为圆为椭圆在时的特例奎屯王新敞新疆椭圆变扁,直至成为极限位置线段,此时也可认为圆为椭圆在时的特例奎屯王新敞新疆【典型例题】例1.写出适合下列条件的椭圆的标准方程:(1)两个焦点坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点的距离之和等于10;⑵两个焦点坐标分别是(0,-2)和(0,2)且过(,)奎屯王新敞新疆解:(1)因为椭圆的焦点在轴上,所以设它的标准方程为用心爱心专心115号编辑所以所求椭圆标准方程为奎屯王新敞新疆(2)因为椭圆的焦点在轴上,所以设它的标准方程为由椭圆的定义知,+又所以所求标准方程为奎屯王新敞新疆例2.求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标,并用描点法画出它的图形.解:把已知方程化成标准方程所以,,因此,椭圆的长轴的长和短轴的长分别为,离心率,两个焦点分别为,椭圆的四个顶点是,奎屯王新敞新疆将已知方程变形为,根据,在的范围内算出几个点的坐标:先描点画出椭圆的一部分,再利用椭圆的对称性画出整个椭圆:01234543.93.73.22.40例3.求适合下列条件的椭圆的标准方程.(1)焦点在轴上,且经过点(2,0)和点...