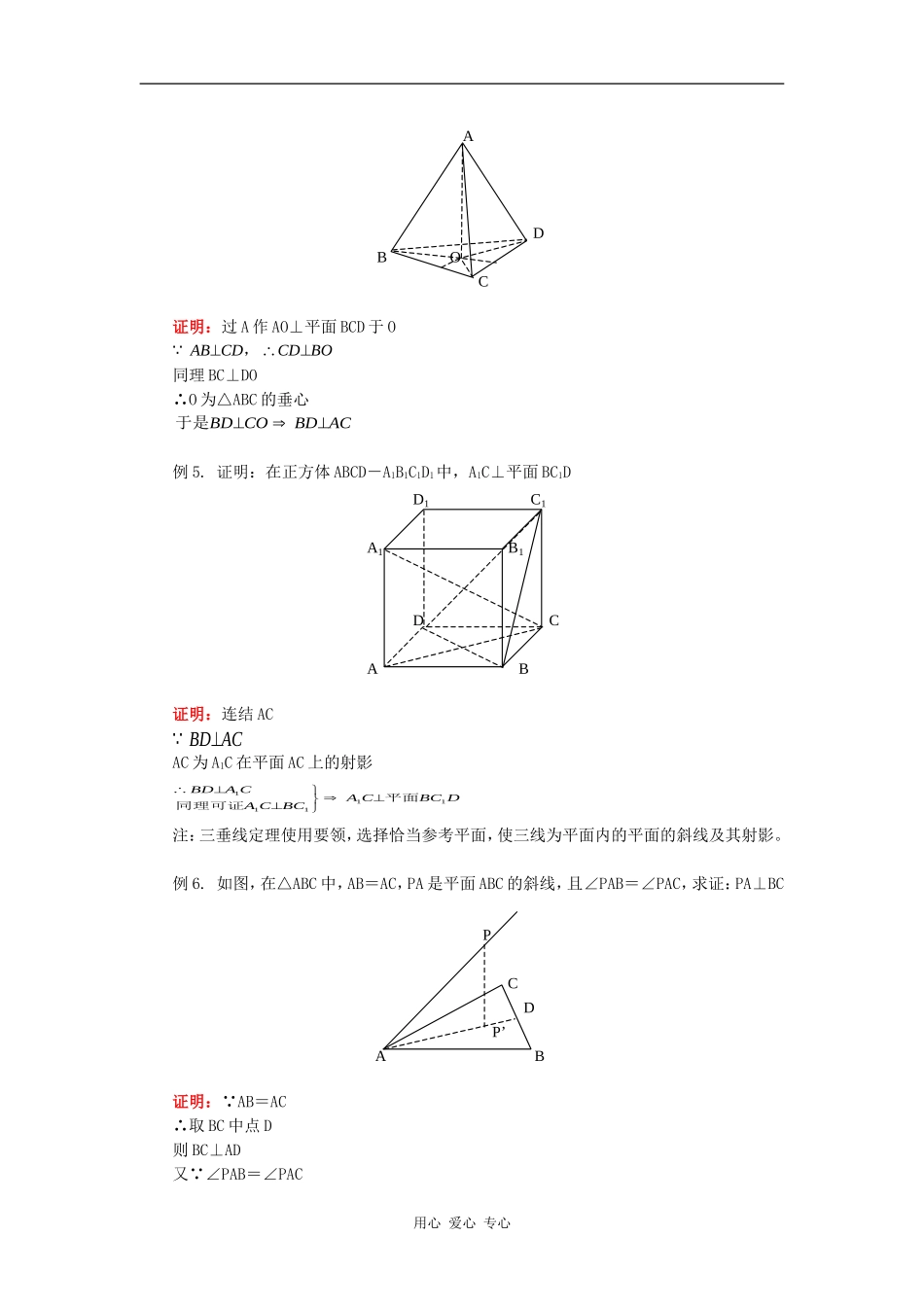
高二数学线、面垂直人教版【本讲教育信息】一.教学内容:线、面垂直目标:掌握线、面垂直的定义、判断、性质、三垂线定理及逆定理。二.重点、难点重点:判定定理、三垂线定理及逆定理。难点:三垂线定理及逆定理的应用,线、面垂直的判定及应用。知识点:1.线、面垂直定义:若直线l垂直于平面α内的任一直线,则l⊥α。2.线、面垂直的判定定理:若直线与平面内两条相交直线垂直,则直线与平面垂直。3.线、面垂直的性质定理:()若,则1lla()若,且,则21212llll//()若,且,则31212llll//4.三垂线定理:已知,为的斜线,为在内的射影,若,则。alllalal''三垂线定理的逆定理:若,则(已知同上)alal'注:讨论两直线垂直可选定一参考平面α使其中一线在内,一线为α的斜线。【典型例题】例1.若,且,求证:llll1212//l1l2a证明:设a为α内任一直线lla11,则又,llla212//用心爱心专心l2例2.设ABCD是空间四边形,若AB=AD,CB=CD,求证:AC⊥BDADEBC证明: AB=AD,BC=DC∴取BD中点E则BDAEBDCEBDAECBDAC平面,例3.已知O是△ABC的外心,P是△ABC所在平面外一点,且PA=PB=PC,求证:PO⊥平面ABC证明:过P作PO’⊥平面ABC于O’PAPBPCPCAOBOAOCOB'''OO'与重合于是POABC平面例4.空间四边形ABCD中,若AB⊥CD,BC⊥AD,求证:AC⊥BD用心爱心专心ADBOC证明:过A作AO⊥平面BCD于OABCDCDBO,同理BC⊥DO∴O为△ABC的垂心于是BDCOBDAC例5.证明:在正方体ABCD-A1B1C1D1中,A1C⊥平面BC1DD1C1A1B1DCAB证明:连结ACBDACAC为A1C在平面AC上的射影BDACACBCACBCD11111同理可证平面注:三垂线定理使用要领,选择恰当参考平面,使三线为平面内的平面的斜线及其射影。例6.如图,在△ABC中,AB=AC,PA是平面ABC的斜线,且∠PAB=∠PAC,求证:PA⊥BCPCDP’AB证明: AB=AC∴取BC中点D则BC⊥AD又 ∠PAB=∠PAC用心爱心专心∴AP在平面ABC内射影在AD上∴由三垂线定理得:BC⊥PA【模拟试题】一.选择题1.过直线l外的两点作与l平行的平面,则这样的平面()A.不可能作出B.只能作一个C.能作出无数个D.以上情况都有可能2.下面四个命题正确的个数是()①如果a、b是两条直线且a//b,那么a平行于经过b的任何一个平面;②如果直线a和平面满足a//,那么a与内的任何直线都平行;③如果直线a、b和平面满足a//,b//,那么直线a//b④如果直线a、b和平面满足a//b,a//,那么b//A.0个B.1个C.2个D.3个3.如果点M是两条异面直线外一点,则过M且与a、b都平行的平面()A.只有一个B.恰有两个C.没有或只有一个D.有无数个4.在下列条件中,可判定平面与平面平行的是()A.、都垂直于平面B.内不共线的三个点到的距离相等C.lm、是内两条直线,且lm////,D.lm、是两异面直线且lmlm////////,,且,5.给出下列四个命题:①若两个平面没有公共点,则这个平面平行;②平行于同一直线的两个平面平行;③垂直于同一直线的两个平面平行;④平行于同一平面的两个平面平行。其中正确的命题是()A.①②③④B.②③④C.①③④D.①②③二.填空题6.正方体ABCD-A1B1C1D1的棱长为1,过A1C1且平行于对角线B1D的截面的面积等于____________7.已知直线a、b为异面直线,点A、B在直线a上,点C、D在直线b上,且AC=AD,BC=BD,则直线a、b所成的角为__________8.正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过A、C、E的平面的位置关系是____________三.解答题9.已知平面//平面,A、C,BD、,点E、F分别在线段AB、CD上,且AEEBCFFD,求用心爱心专心证:EF//10.如图,点P为长方形ABCD所在平面外一点,M、N分别是AB、PD上的点,且AM:MB=DN:NP,求证:MN//平面PBCPNDCAMB11.如图,PA平面ABCD,ABCD是矩形,M、N分别是AB、PC的中点,求证:MNABPNDCABM附加题:如图,已知空间四边形ABCD的边AC=BC,AD=BD,引BECD,E为垂足,作AHBE于H,求证:AH平面BCDABDHEC用心爱心专心试题答案一.选择题1.D2.A3.C4.D5.C二.填空题...