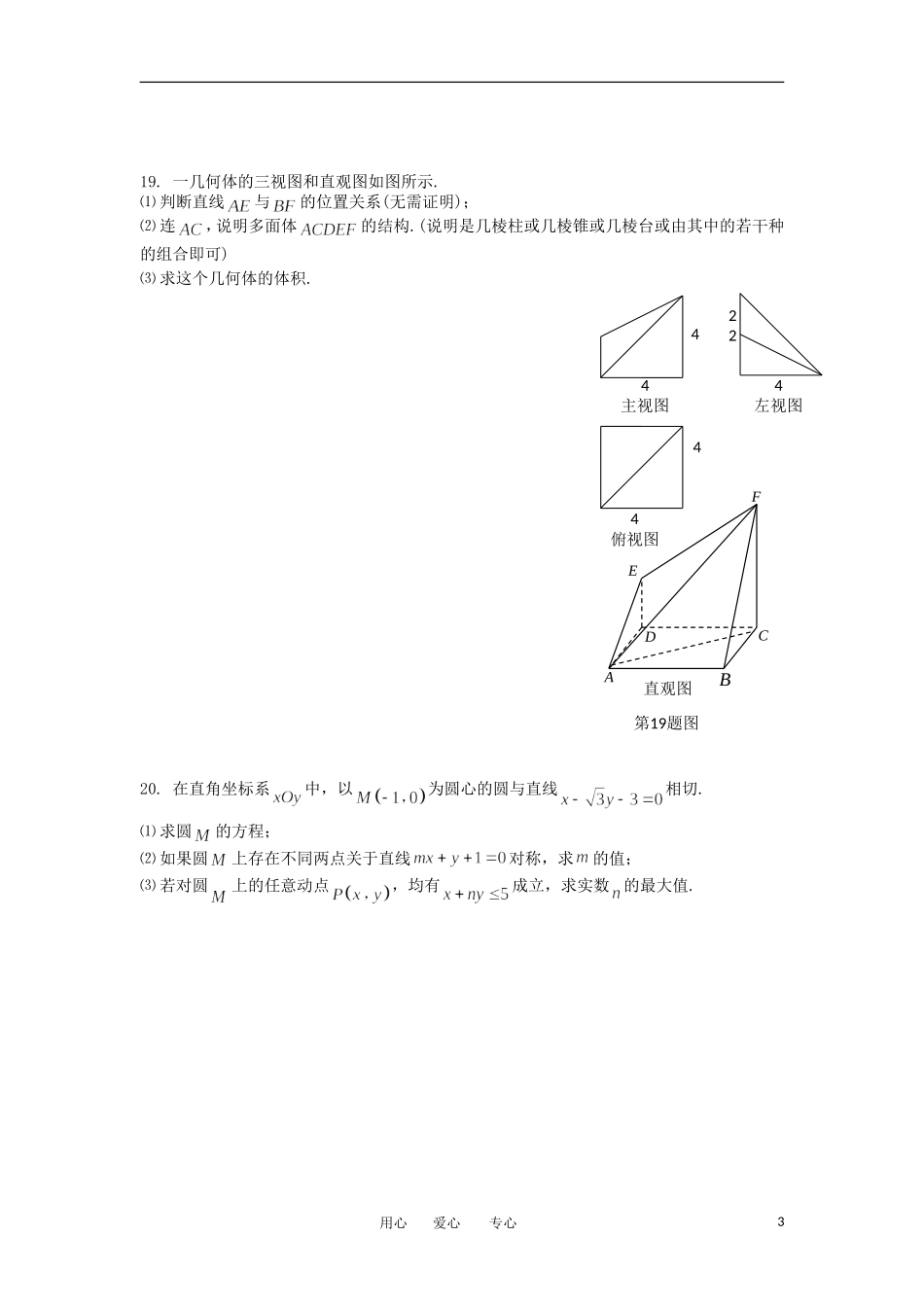
浙江省湖州市2011学年上学期高二数学期终样卷一、选择题1.抛物线的焦点坐标是A.B.C.D.2.若集合,则“”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知是椭圆的两个焦点,是该椭圆过的弦,且满足,则等于A.B.C.D.4.过点且倾斜角为的直线被圆所截得的弦长为A.B.C.D.5.设是两条不同的直线,是两个不同的平面,下列命题正确的是A.若,则B.若,则C.若,则D.若,则6.表面积为的圆锥的侧面展开图为半圆,则圆锥的底面半径为A.B.C.D.7.直线的倾斜角的范围是A.B.C.D.8.已知三棱柱的侧棱与底面边长都相等,在底面内的射影为的中心,则与底面所成角的正弦值等于A.B.C.D.9.点是抛物线上一动点,则点到点的距离与到直线的距离和的最小值是A.B.C.D.10.如图,是平面的一条斜线段,为斜足,与成,且,上的动点用心爱心专心1ABC1A1B1CO第8题图满足到的距离为,则动点的轨迹为A.直线B.圆C.抛物线D.椭圆二、填空题11.直线与的距离是_________.12.点关于直线的对称点的坐标是.13.在空间直角坐标系中,已知的坐标分别为,则线段在坐标平面上的射影的长度为______________.14.中,,,以为焦点的双曲线过的顶点,则双曲线的离心率为_________.15.在正方体中,是棱上一点,且,则异面直线与所成角的余弦值为_________.16.已知直线,的交点在一个定圆上,则该圆的标准方程为____________.17.已知是球表面上的点,平面,,,,则球的表面积等于______________.(球的表面积为)三、解答题18.已知命题,命题,若是的必要不充分条件,求实数的取值范围.用心爱心专心2ABP第10题图19.一几何体的三视图和直观图如图所示.⑴判断直线与的位置关系(无需证明);⑵连,说明多面体的结构.(说明是几棱柱或几棱锥或几棱台或由其中的若干种的组合即可)⑶求这个几何体的体积.20.在直角坐标系中,以为圆心的圆与直线相切.⑴求圆的方程;⑵如果圆上存在不同两点关于直线对称,求的值;⑶若对圆上的任意动点,均有成立,求实数的最大值.用心爱心专心34俯视图444左视图224主视图第19题图ABCDEF直观图21.如图,四边形为矩形,平面,,为上的点,且平面.⑴设分别在线段上,且满足,求证:平面;⑵求证:;⑶求二面角的大小.22.椭圆的中心在原点,短轴长为,长轴长为,左焦点为,直线与轴交于点,且.⑴求椭圆的方程;⑵设直线与椭圆交于两点,点关于轴的对称点为.试问当变化时,直线是否经过轴上的定点?若是,写出定点坐标,并证明你的结论;若不是,请说明理由.一、选择题题号12345678910答案CACCCACBDD二、填空题11.12.13.14.15.16.17.三、解答题18.解:由已知得得;用心爱心专心4第21题图ABCDFNEM得.由是的必要不充分条件,即是的充分不必要条件,得,的取值范围是.19.解:⑴和是异面直线;⑵多面体是以为顶点,为底面的四棱锥;⑶由三视图知直观图中,平面,平面,底面为边长为的正方形,,平面,面为直角梯形,,所以几何体的体积为.20.解:⑴的半径,的方程为;⑵由已知得直线过,⑶令,则由题意知直线与圆有公共点,所以到其距离不大于半径,即,故依题意有,所以的最大值为.21.⑴证明:在上取靠近的三等分点,连,则由知,又,,平面,平面,所以平面,同理:平面,又平面,所以平面平面,而平面,所以平面;用心爱心专心54左视图44主视图4224俯视图第19题图ABCDEF直观图MABCDFENO⑵证明:平面,平面,平面,平面,平面,平面,平面,平面,.⑶由⑵知可如图建立空间直角坐标系,因为,故取中点,可得为平面的法向量,因为,平面,所以为平面的法向量,又在上,故为中点.在所建立的坐标系下,各点的坐标为,所以点的坐标为,点的坐标为,即,,所以二面角的余弦值为,所以二面角为.22.解:⑴由,即,又,椭圆的方程为.⑵化为,令,得直线过定点,由知该直线斜率存在,故可设其方程为,联立消,得,设,则,且.由直线斜率,得直线的方程为,令,得,将用心爱心专心6ABCDFNEMxyzP代入,得,即无论也即如何变化,直线过定点.⑵另解:化为,令,得直线过定点,不妨将其改变形式为,由知.由消,得,设,则,且.由直线斜率,得直线的方程为,令,得,将代入,得,即无论也即如何变化,直线过定点.用心爱心专心7