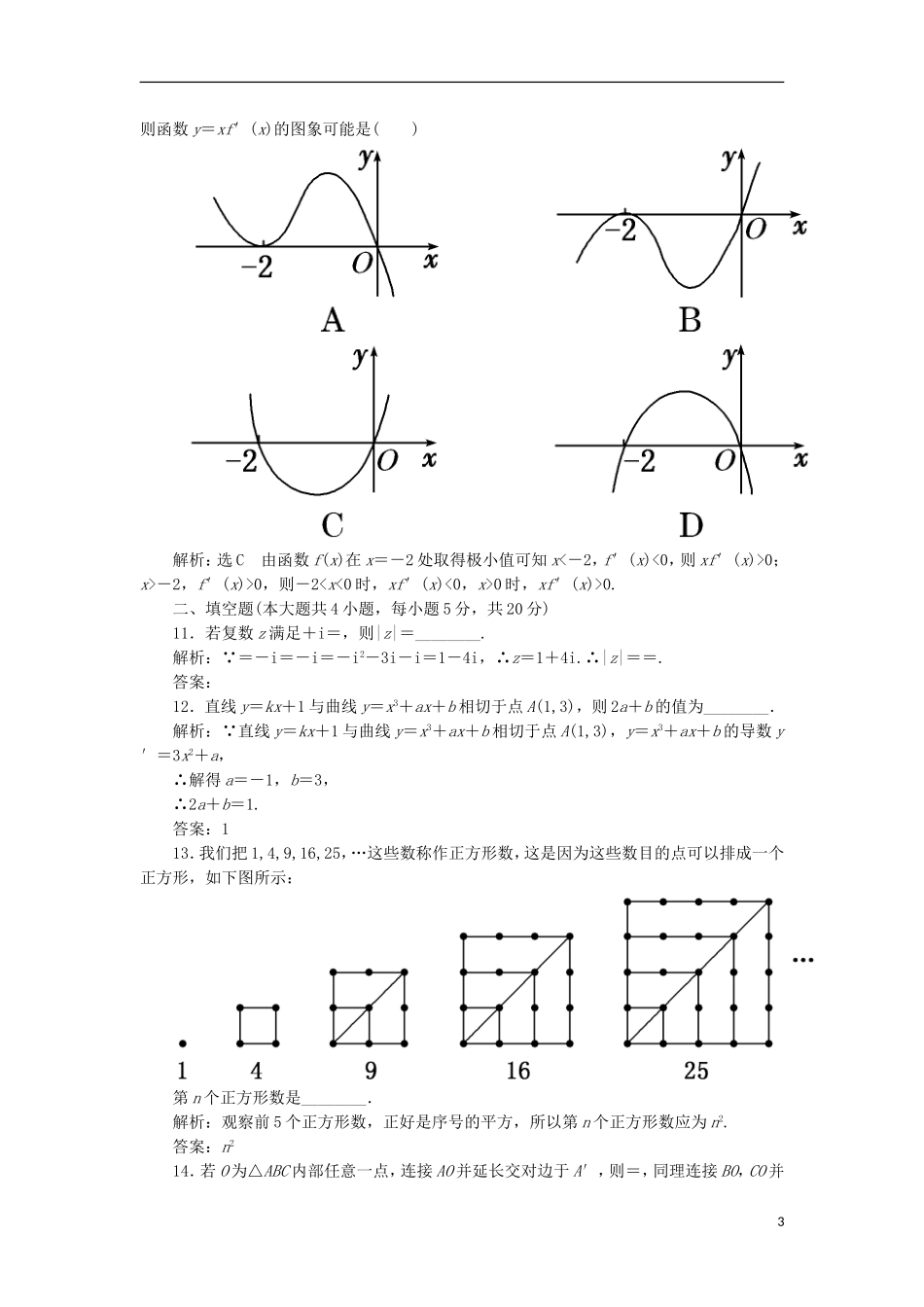
模块综合检测(一)(时间120分钟,满分150分)一、选择题(本大题共10小题,每小题5分,共50分)1.设z=,则z的共轭复数为()A.-1+3iB.-1-3iC.1+3iD.1-3i解析:选D z===1+3i,∴=1-3i.2.若函数f(x)=excosx,则此函数的图象在点(1,f(1))处的切线的倾斜角为()A.0B.锐角C.D.钝角解析:选Df′(x)=ex·cosx+ex·(-sinx)=ex(cosx-sinx).当x=1时,cosx-sinx<0,故f′(1)<0,所以倾斜角为钝角.3.用反证法证明命题“若函数f(x)=x2+px+q,那么|f(1)|,|f(2)|,|f(3)|中至少有一个不小于”时,反设正确的是()A.假设|f(1)|,|f(2)|,|f(3)|都不小于B.假设|f(1)|,|f(2)|,|f(3)|都小于C.假设|f(1)|,|f(2)|,|f(3)|至多有两个小于D.假设|f(1)|,|f(2)|,|f(3)|至多有一个小于解析:选B“|f(1)|,|f(2)|,|f(3)|中至少有一个不小于”的反设为“|f(1)|,|f(2)|,|f(3)|都小于”.4.设a=x-dx,b=1-xdx,c=x3dx,则a,b,c的大小关系为()A.a>b>cB.b>a>cC.a>c>bD.b>c>a解析:选A由题意可得a=x-dx==x=;b=1-xdx=1-=1-=;c=x3dx==.综上可得,a>b>c.5.由①y=2x+5是一次函数;②y=2x+5的图象是一条直线;③一次函数的图象是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是()A.②①③B.③①②C.①②③D.②③①解析:选B该“三段论”应为:一次函数的图象是一条直线(大前提),y=2x+5是一次函数(小前提),y=2x+5的图象是一条直线(结论).6.如下图,我们知道,圆环也可以看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×.所以,圆环的面积等于以线段AB=R-r为宽,以AB的中点绕圆心O旋转一周所形成的圆的周长2π×为长的矩形面积.请你将上述想法拓展到空间,并解决下列问题:若将平面区域M=(其中00,类比可得方程ax2+bx+c=0(a,b,c∈C且a≠0)有两个不同的复数根的条件是b2-4ac>0;④由向量加法的几何意义,可以类比得到复数加法的几何意义.其中类比得到的结论正确的是()A.①③B.②④C.②③D.①④解析:选D②中|z|2∈R,但z2不一定是实数.③中复数集不能比较大小,不能用b2-4ac来确定根的个数.9.设x>0,y>0,A=,B=+,则A与B的大小关系为()A.A>BB.A≥BC.A<BD.A≤B解析:选C+>+=.10.设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=-2处取得极小值,2则函数y=xf′(x)的图象可能是()解析:选C由函数f(x)在x=-2处取得极小值可知x<-2,f′(x)<0,则xf′(x)>0;x>-2,f′(x)>0,则-20时,xf′(x)>0.二、填空题(本大题共4小题,每小题5分,共20分)11.若复数z满足+i=,则|z|=________.解析: =-i=-i=-i2-3i-i=1-4i,∴z=1+4i.∴|z|==.答案:12.直线y=kx+1与曲线y=x3+ax+b相切于点A(1,3),则2a+b的值为________.解析: 直线y=kx+1与曲线y=x3+ax+b相切于点A(1,3),y=x3+ax+b的导数y...