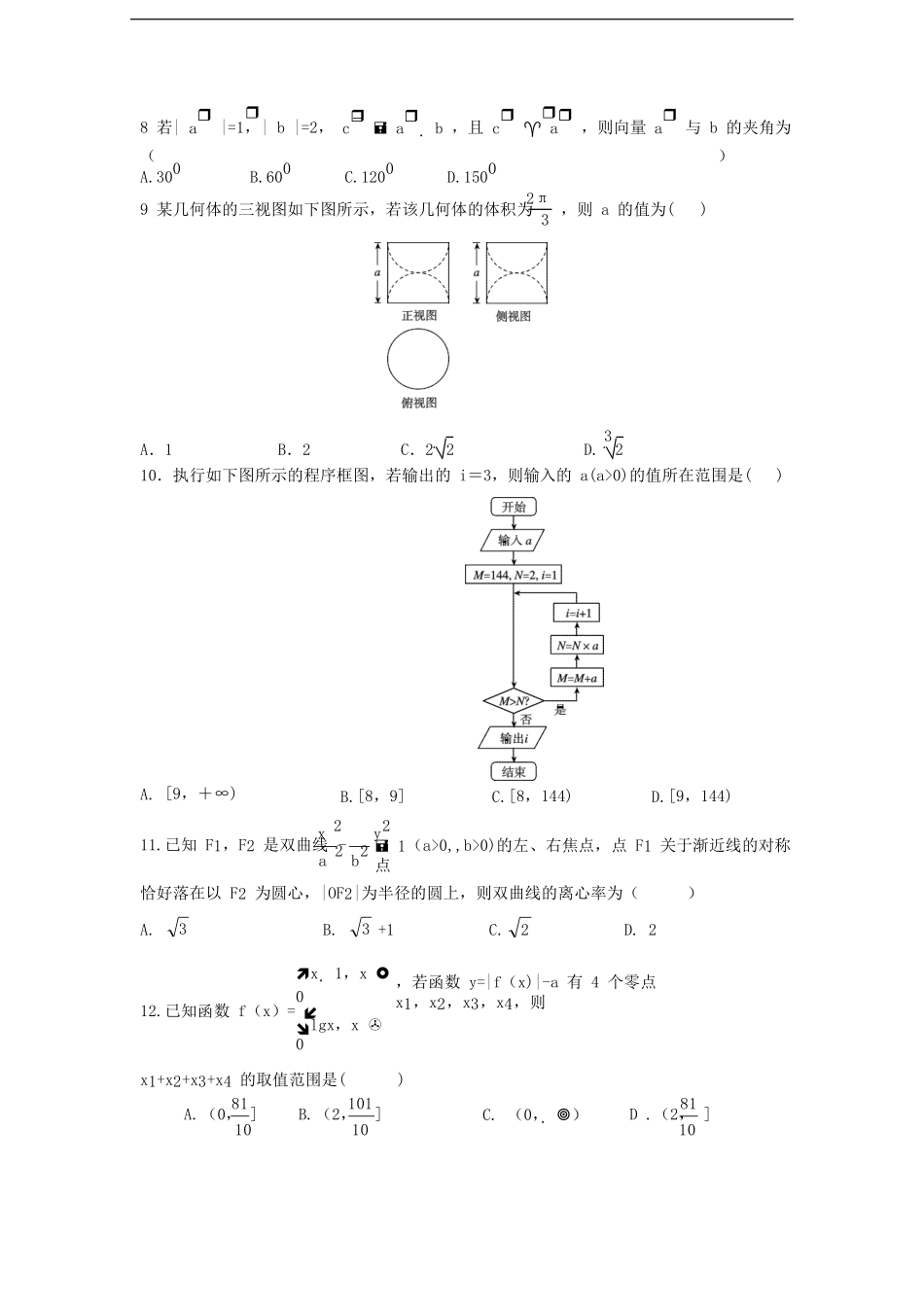
2017年上学期湘东五校联考高二年级期末考试理科数学试题时间:120分钟满分:150分一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x2+4x+3≥0},B={x|2x<1},则A∩B=()A.[-3,-1]B.(-∞,-3]∪[-1,0)C.(-∞,-3)∪(-1,0]D.(-∞,0)3+i2.已知复数z=,其中i为虚数单位,则|z|=()2(1+i)1A.2B.1C.2D.2x3.设命题p:若x,y∈R,x=y,则=1;命题q:若函数f(x)=ex,则对任意x≠x都有y12f(x1)-f(x2)x1-x2()>0成立.在命题①p∧q,②p∨q,③p∧q,④p∨q中,是真命题的是A.①③B.①④C.②③D.②④4.椭圆x2+my2=1的长轴长为4,则其焦点坐标为()A.(3,0)B.(1,0)C.(0,1)D.(0,3)5.甲乙丙三人相约晚7时到8时之间在某地会面,已知这三人都不会违约且无两人同时到达,则甲第一个到达,丙第三个到达的概率为()1111A.B.C.D.34566.我国古代数学名著《张邱建算经》:今有与人钱,初一人与三钱,次一人与四钱,次一人与五钱,以次与之,转多一钱,与讫,还敛聚与均分之,人得一百钱,问人几何?意思是:将钱分给若干人,第一人给3钱,第二人给4钱,第3人给5钱,以此类推,每人比前一人多给1钱,分完后,再把钱收回平均分给各人,结果每人分得100钱,问有多少人?则题中的人数是()A.193B.194C.195D.1967.函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图像如下图所示,则f11π的值为()246A.-23B.-22C.-2D.-118若|a|=1,|b|=2,cab,且ca,则向量a与b的夹角为()A.300B.600C.1200D.15002π9某几何体的三视图如下图所示,若该几何体的体积为3,则a的值为()3A.1B.2C.22D.210.执行如下图所示的程序框图,若输出的i=3,则输入的a(a>0)的值所在范围是()A.[9,+∞)B.[8,9]x2y2C.[8,144)D.[9,144)11.已知F1,F2是双曲线-a2b21(a>0,,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则双曲线的离心率为()A.3B.3+1C.2D.2x1,x012.已知函数f(x)=lgx,x0,若函数y=|f(x)|-a有4个零点x1,x2,x3,x4,则x1+x2+x3+x4的取值范围是()8110181A.(0,]10B.(2,]10C.(0,)D.(2,]10第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13.函数f(x)=ax+lnx在x=1处的切线与直线x-y+1=0垂直,则实数a=314.1x-2x12的展开式的常数项为15.在ABC中,已知AB=3,C=,则CACB的最大值为316.一个样本容量为20的样本数据,它们组成一个公差不为0的等差数列{an},若a2=6且前4项和为S4=28,则此样本数据的平均数和中位数分别为、三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题12分)已知数列{an}的前n项和为Sn,Sn=2an-1,数列{bn}为等差数列,且b1=a1,b6=a5(1)求数列{an}与{bn}的通项公式;(2)若Cn=anbn,求数列{cn}的前n项和Tn。18.(本小题12分)如图所示,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.(1)求证:AF⊥EF;(2)求二面角A•PC•B的平面角的正弦值.19.(本小题12分)有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布表如下:所用的时间(天数)10111213通过公路1的频数20402020通过公路2的频数10404010假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发(将频率视为概率).(1)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径?(2)若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元(其他费用忽略不计),此项费用由生产商承担.若生产商...