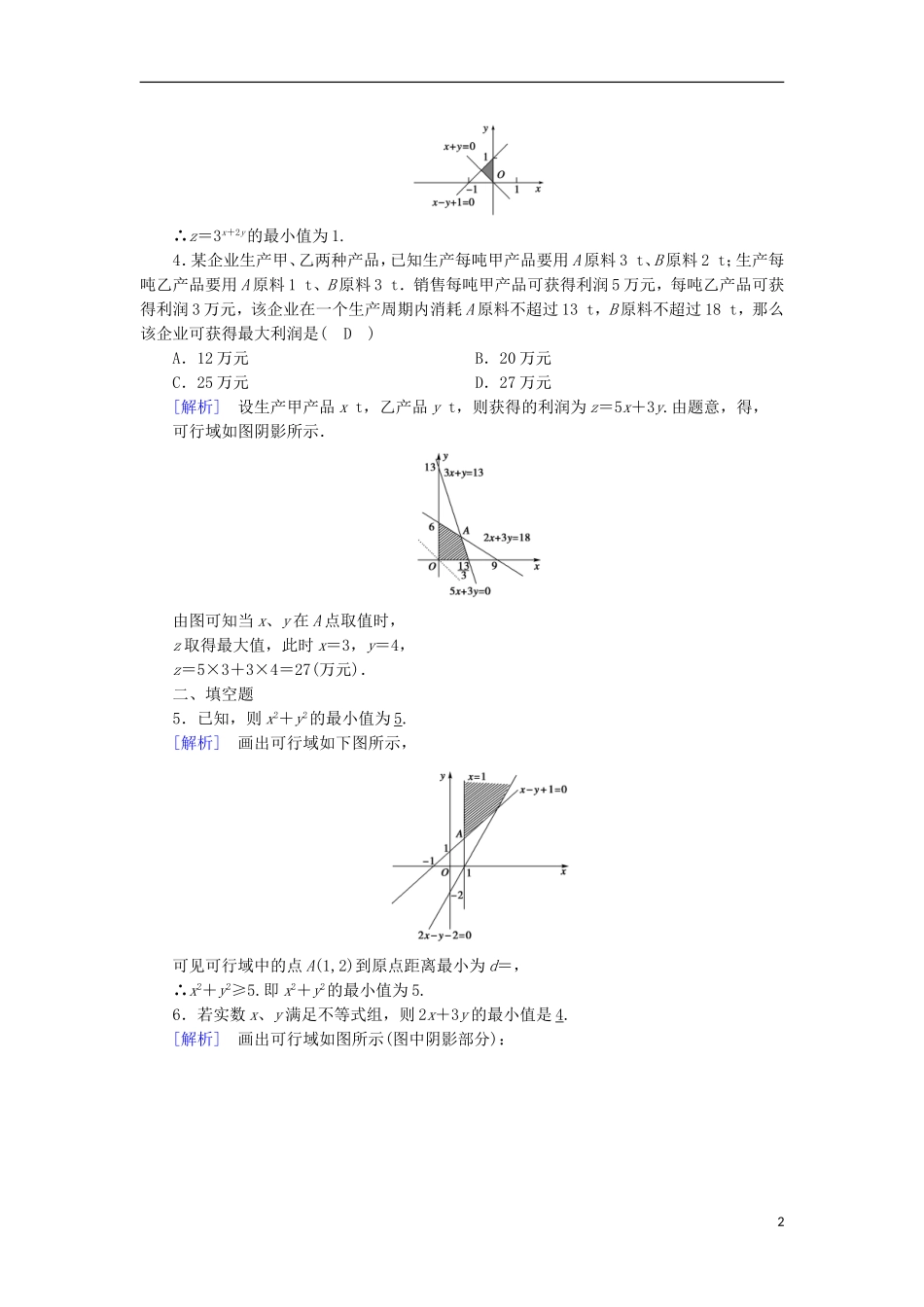
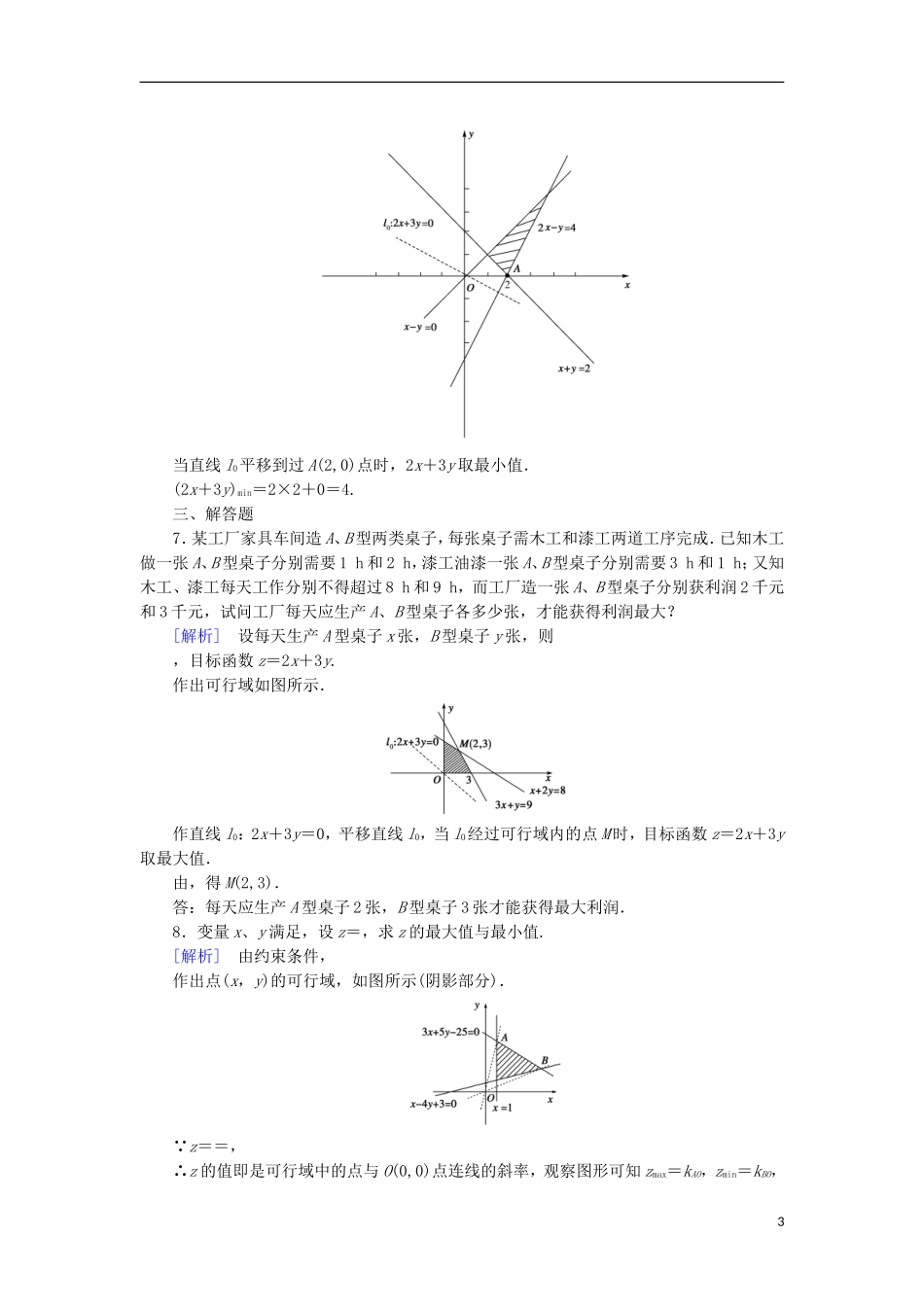
2017春高中数学第3章不等式3.5二元一次不等式(组)与简单的线性规划问题第3课时简单的线性规划的应用课时作业新人教B版必修5基础巩固一、选择题1.已知O为坐标原点,点M(3,1),若N(x,y)满足不等式组,则OM·ON的最大值为(D)A.6B.8C.10D.12[解析]目标函数为z=OM·ON=3x+y,作出不等式组表示的可行域,如图所示.作出直线l0:3x+y=0,再将直线l0平移,当l0的平行线l1经过点A(4,0)时,z取得最大值12,即OM·ON的最大值为12.2.设变量x、y满足约束条件,则目标函数z=4x+2y的最大值为(B)A.12B.10C.8D.2[解析]画出可域如图中阴影部分所示,目标函数z=4x+2y可转化为y=-2x+,作出直线y=-2x并平移,显然当其过点A时纵截距最大.解方程组得A(2,1),∴zmax=10.3.若实数x、y满足,则z=3x+2y的最小值是(B)A.0B.1C.D.9[解析]由已知不等式组作可行域,如图阴影部分所示,令x+2y=k,则y=-x+,问题由求z的最小值转化为求直线y=-x+的纵截距的最小值.显然当直线y=-x+过原点O时,纵截距最小,此时k=0,1∴z=3x+2y的最小值为1.4.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3t、B原料2t;生产每吨乙产品要用A原料1t、B原料3t.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13t,B原料不超过18t,那么该企业可获得最大利润是(D)A.12万元B.20万元C.25万元D.27万元[解析]设生产甲产品xt,乙产品yt,则获得的利润为z=5x+3y.由题意,得,可行域如图阴影所示.由图可知当x、y在A点取值时,z取得最大值,此时x=3,y=4,z=5×3+3×4=27(万元).二、填空题5.已知,则x2+y2的最小值为5.[解析]画出可行域如下图所示,可见可行域中的点A(1,2)到原点距离最小为d=,∴x2+y2≥5.即x2+y2的最小值为5.6.若实数x、y满足不等式组,则2x+3y的最小值是4.[解析]画出可行域如图所示(图中阴影部分):2当直线l0平移到过A(2,0)点时,2x+3y取最小值.(2x+3y)min=2×2+0=4.三、解答题7.某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1h和2h,漆工油漆一张A、B型桌子分别需要3h和1h;又知木工、漆工每天工作分别不得超过8h和9h,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?[解析]设每天生产A型桌子x张,B型桌子y张,则,目标函数z=2x+3y.作出可行域如图所示.作直线l0:2x+3y=0,平移直线l0,当l0经过可行域内的点M时,目标函数z=2x+3y取最大值.由,得M(2,3).答:每天应生产A型桌子2张,B型桌子3张才能获得最大利润.8.变量x、y满足,设z=,求z的最大值与最小值.[解析]由约束条件,作出点(x,y)的可行域,如图所示(阴影部分). z==,∴z的值即是可行域中的点与O(0,0)点连线的斜率,观察图形可知zmax=kAO,zmin=kBO,3由,解得A(1,),kAO=.由,解得B(5,2),kBO=.故zmax=,zmin=.能力提升一、选择题1.若变量x、y满足,则z=3x+2y的最大值是(C)A.90B.80C.70D.40[解析]由得可行域如图所示.将l0:3x+2y=0在可行域内平行移动,移动到经过B点时,z=3x+2y取最大值.由,得B点坐标为(10,20),∴zmax=3×10+2×20=70,故选C.2.已知x、y满足,则的最值是(C)A.最大值是2,最小值是1B.最大值是1,最小值是0C.最大值是2,最小值是0D.有最大值无最小值[解析]作出不等式组表示的平面区域如图.表示可行域内点与原点连线的斜率.显然在A(1,2)处取得最大值2.在x轴上的线段BC上时取得最小值0,∴选C.3.不等式组表示的平面区域内整点的个数是(D)A.0B.2C.4D.5[解析]不等式组变形为,即作出其平面区域如图.可见其整点有:(-1,0)、(0,1)、(0,0)、(0,-1)和(1,0)共五个.44.已知x、y满足约束条件,则z=x+y的最大值是(B)A.B.C.2D.4[解析]画出可行域为如图阴影部分.由,解得A(,),∴当直线z=x+y经过可行域内点A时,z最大,且zmax=.二、填空题5.若x、y满足约束条件,则z=2x-y的最大值为9.[解析]约束条件的可行域为如图所示.作l0...