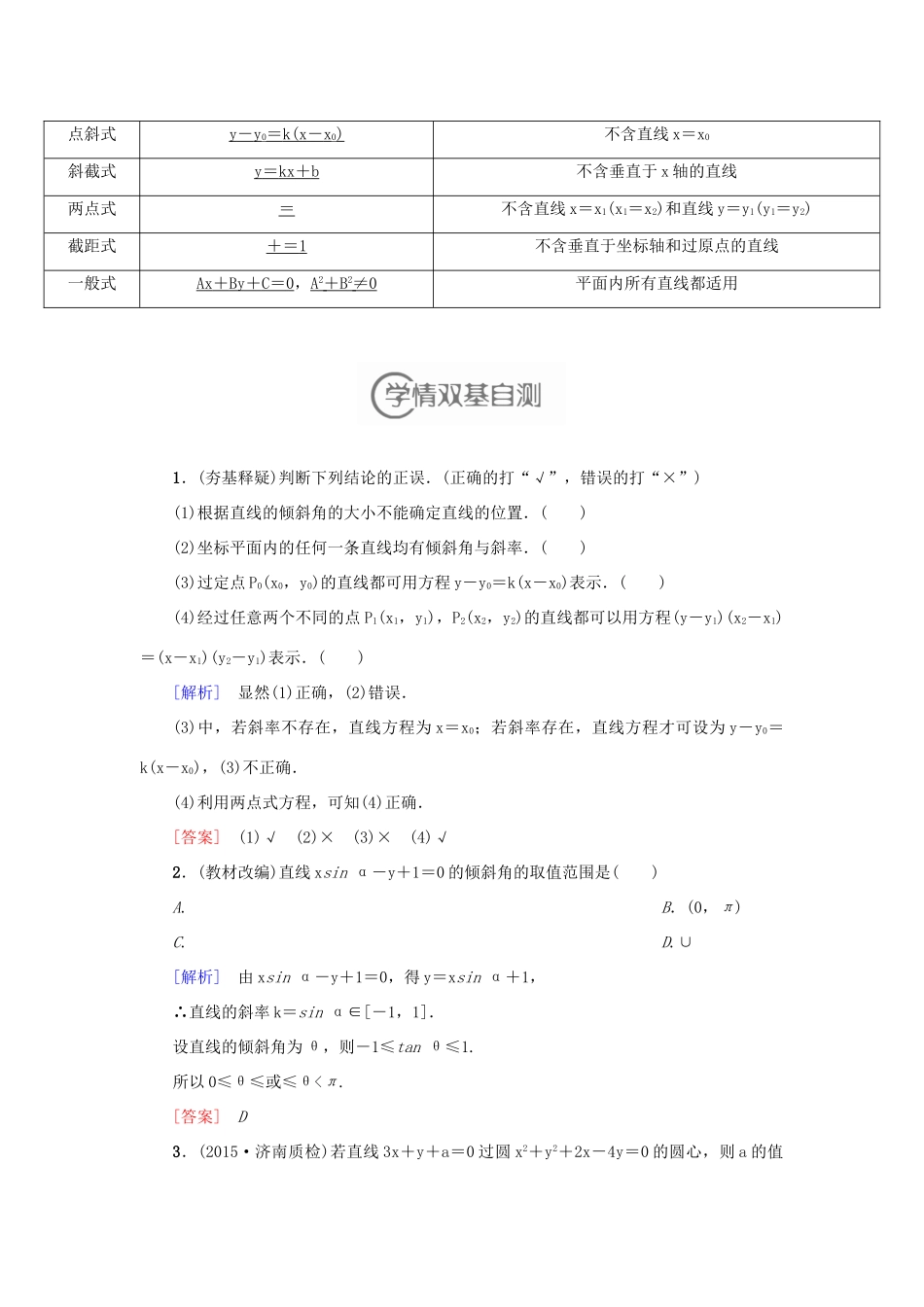
第八章平面解析几何平面解析几何在高考中占有举足轻重的地位,从近几年课标区各省市高考题试卷来看,与本章相关题的分值约22分,占总分值的14%~15%.对直线方程、圆及圆锥曲线的概念和性质的考查一般以选择题或填空如2014·四川14,2014·陕西12,2014·天津5),重在考查学生的双基掌握情况.对直线与圆锥曲线的位置关系的考查,常以压轴题的形式出现,其命题形式常与向量结合,重在考查圆锥曲线的几何性质(2014·课标全国卷2014·福建19,2014·山东10),另外定值问题、最值问题及探索性问题依然是考查的热点问题(如2014·北京19,2014·福建9,2014·山东21等).1.抓主线,构建知识体系,对直线、圆及圆锥曲线的基本定义、标准方程和相关性质应熟练掌握,如对直线与圆锥曲线的位置关系的解法及解题思想应灵活掌握.2.依托基础知识,强化思想方法训练,直线、圆及圆锥曲线是数与形结合的完美载体,要熟练运用坐标法和“数形结合”思想,另外,函数与方程的思想是本章学习的另一个重点,应加强运用.3.加强纵横联系,强化综合应用意识,在知识的交汇处命题,已成为高考的一大亮点,尤其应加强该部分知识与向量、函数、方程及不等式间的内在联系,同时解题中立足通性、通法、淡化技巧以达到优化解题思路化解题过程的目的.本章内容集中体现了两大数学思想:函数与方程及数形结合的思想,且常与向量、三角函数、不等式、导数等知识交汇命题,体现了综合与创4.突出重点,热点考查内容的复习,如轨迹问题,对称问题,定值题、范围问题,开放和探索性问题及向量与解析几何的综合应用问题等等第一节直线的倾斜角与斜率、直线方程[考纲传真]1.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.2.掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.1.直线的倾斜角(1)定义(2)范围[0,π).2.直线的斜率(1)定义:若直线的倾斜角α不是90°,则其斜率k=tan_α;(2)斜率公式:若由A(x1,y1),B(x2,y2)确定的直线不垂直x轴,则k=.3.直线方程的五种形式名称方程适用范围点斜式y-y0=k(x-x0)不含直线x=x0斜截式y=kx+b不含垂直于x轴的直线两点式=不含直线x=x1(x1=x2)和直线y=y1(y1=y2)截距式+=1不含垂直于坐标轴和过原点的直线一般式Ax+By+C=0,A2+B2≠0平面内所有直线都适用1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)根据直线的倾斜角的大小不能确定直线的位置.()(2)坐标平面内的任何一条直线均有倾斜角与斜率.()(3)过定点P0(x0,y0)的直线都可用方程y-y0=k(x-x0)表示.()(4)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.()[解析]显然(1)正确,(2)错误.(3)中,若斜率不存在,直线方程为x=x0;若斜率存在,直线方程才可设为y-y0=k(x-x0),(3)不正确.(4)利用两点式方程,可知(4)正确.[答案](1)√(2)×(3)×(4)√2.(教材改编)直线xsinα-y+1=0的倾斜角的取值范围是()A.B.(0,π)C.D.∪[解析]由xsinα-y+1=0,得y=xsinα+1,∴直线的斜率k=sinα∈[-1,1].设直线的倾斜角为θ,则-1≤tanθ≤1.所以0≤θ≤或≤θ<π.[答案]D3.(2015·济南质检)若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心,则a的值为()A.-1B.1C.3D.-3[解析]圆的方程(x+1)2+(y-2)2=5,圆心为(-1,2). 直线过圆心,∴3×(-1)+2+a=0,∴a=1.[答案]B4.(2014·福建高考)已知直线l过圆x2+(y-3)2=4的圆心,且与直线x+y+1=0垂直,则直线l的方程是()A.x+y-2=0B.x-y+2=0C.x+y-3=0D.x-y+3=0[解析]圆x2+(y-3)2=4的圆心为点(0,3),又因为直线l与直线x+y+1=0垂直,所以直线l的斜率k=1.由点斜式得直线l:y-3=x-0,化简得x-y+3=0.[答案]D5.直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则实数a=________.[解析]令x=0,则l在y轴上的截距为2+a;令y=0,得直线l在x轴上的截距为1+.依题意2+a=1+,解得a=1或a=-2.[答案]1或-2考向1直线的倾斜角和斜率【典例...