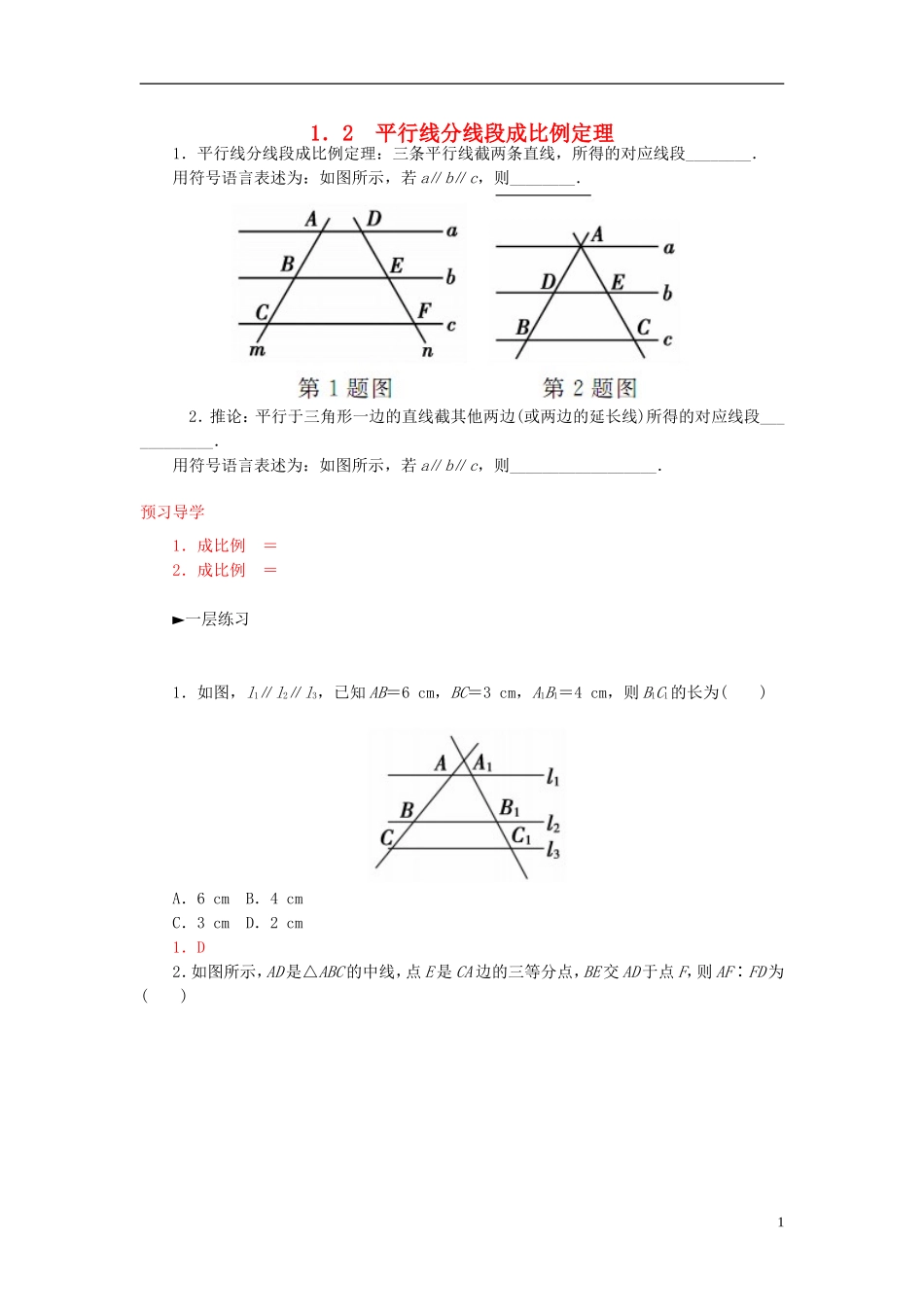
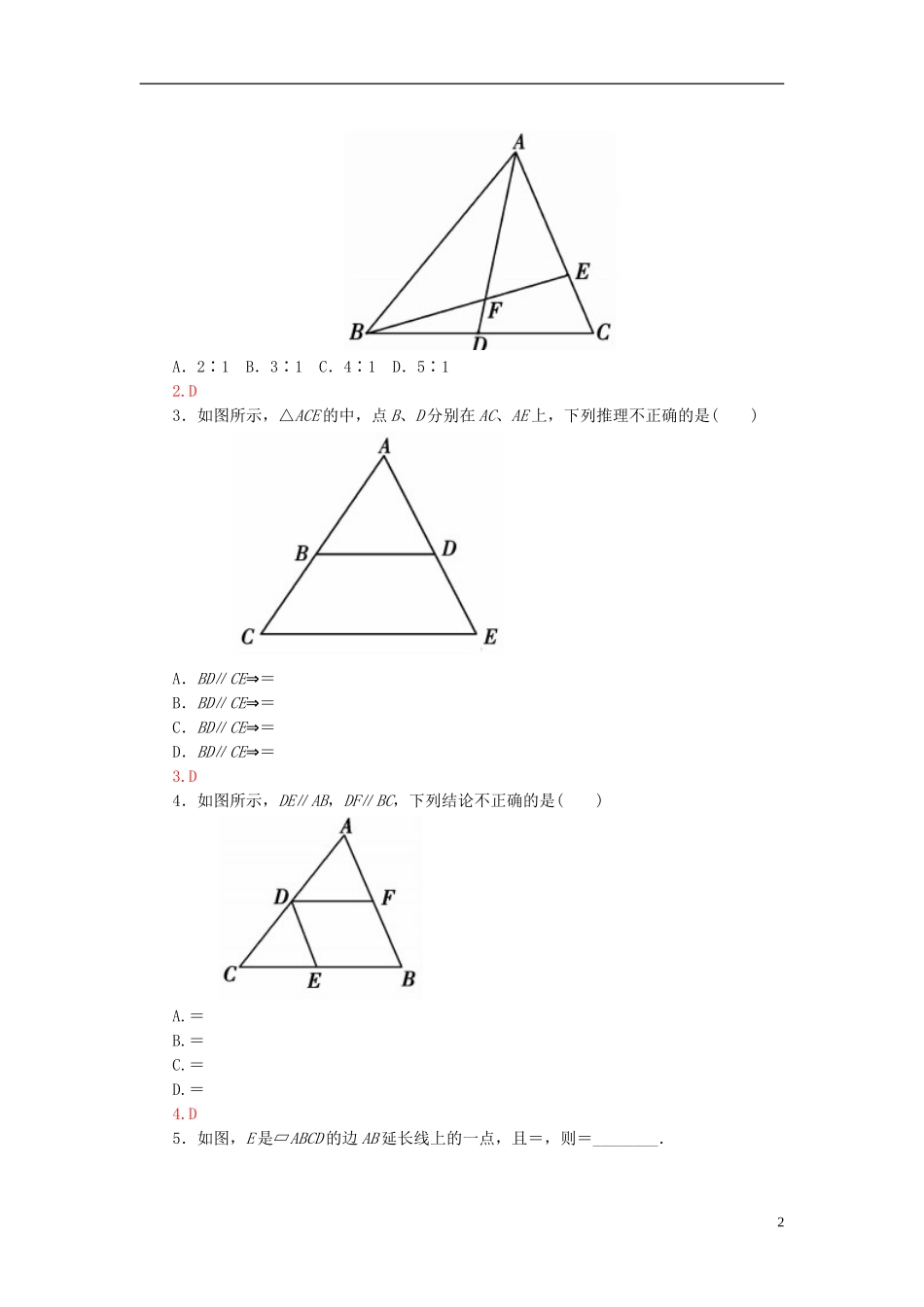
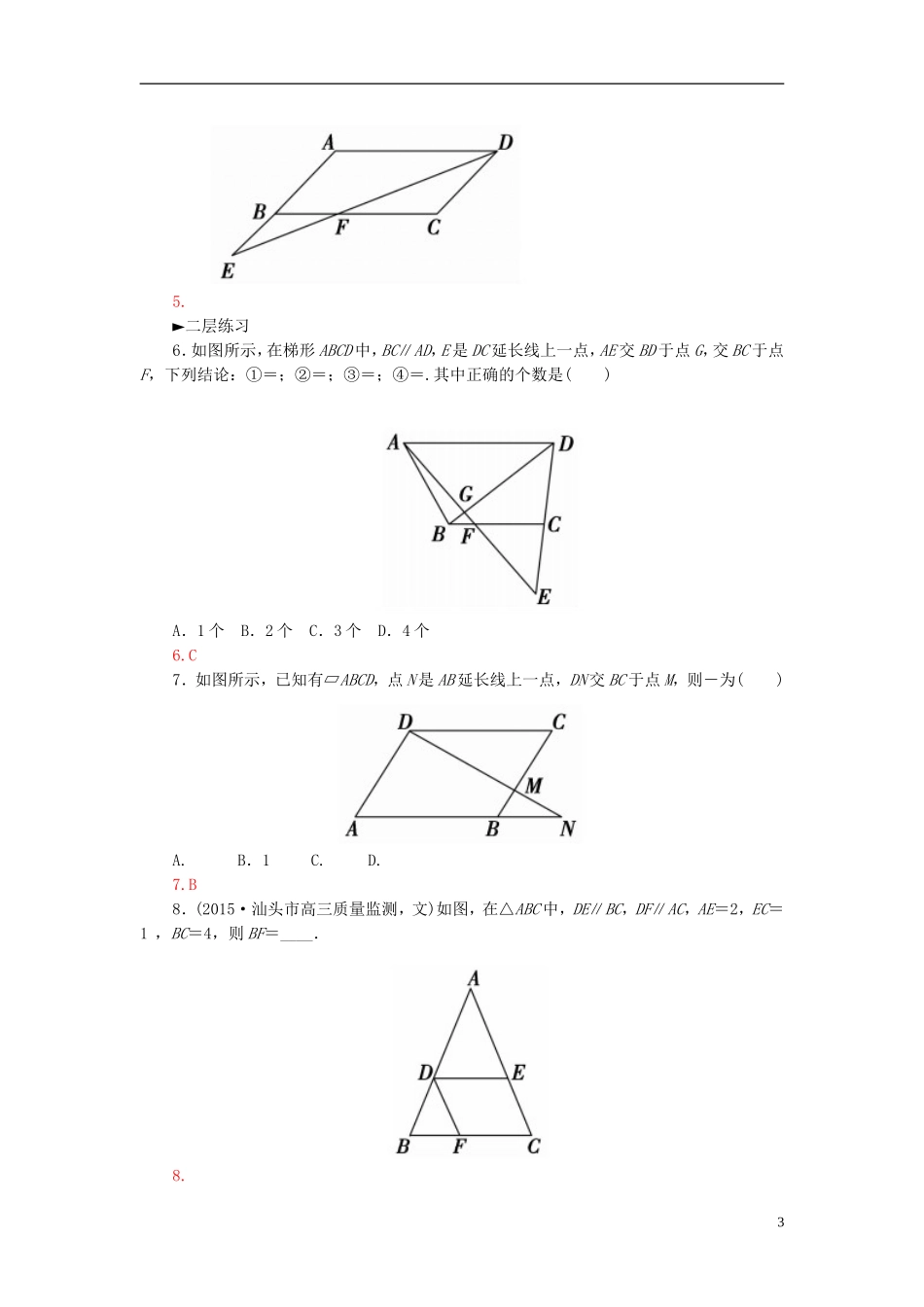
1.2平行线分线段成比例定理1.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段________.用符号语言表述为:如图所示,若a∥b∥c,则________.2.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段____________.用符号语言表述为:如图所示,若a∥b∥c,则__________________.预习导学1.成比例=2.成比例=►一层练习1.如图,l1∥l2∥l3,已知AB=6cm,BC=3cm,A1B1=4cm,则B1C1的长为()A.6cmB.4cmC.3cmD.2cm1.D2.如图所示,AD是△ABC的中线,点E是CA边的三等分点,BE交AD于点F,则AF∶FD为()1A.2∶1B.3∶1C.4∶1D.5∶12.D3.如图所示,△ACE的中,点B、D分别在AC、AE上,下列推理不正确的是()A.BD∥CE⇒=B.BD∥CE⇒=C.BD∥CE⇒=D.BD∥CE⇒=3.D4.如图所示,DE∥AB,DF∥BC,下列结论不正确的是()A.=B.=C.=D.=4.D5.如图,E是▱ABCD的边AB延长线上的一点,且=,则=________.25.►二层练习6.如图所示,在梯形ABCD中,BC∥AD,E是DC延长线上一点,AE交BD于点G,交BC于点F,下列结论:①=;②=;③=;④=.其中正确的个数是()A.1个B.2个C.3个D.4个6.C7.如图所示,已知有▱ABCD,点N是AB延长线上一点,DN交BC于点M,则-为()A.B.1C.D.7.B8.(2015·汕头市高三质量监测,文)如图,在△ABC中,DE∥BC,DF∥AC,AE=2,EC=1,BC=4,则BF=____.8.39.如下图(左)所示,在△ABC中,DE∥BC,EF∥CD,且AB=2,AD=,则AF=________.9.110.如上图(右),E,F是梯形ABCD的腰AD,BC上的点,其中CD=2AB,EF∥AB,若=,则=________.10.解析:过A作AH∥BC,交EF、CD于G、H.设AB=a,CD=2a,则=.有EF=a.由EF∥AB∥CD得====-1.又AD=AE+ED,故=-1,得=.答案:11.如图所示,BD∶DC=5∶3,E为AD的中点,求BE∶EF的值.11.解析:4过D作DG∥CA交BF于G,则==. E为AD的中点,DG∥AF,∴△DGE≌△AFE,EG=EF.∴===2×=.故==+1=+1=.►三层练习12.如图,在梯形ABCD中,AB∥CD,AB=4,CD=2,E,F分别为AD,BC上的点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比为________.12.13.在△ABC中,D是边AC的中点,点E在线段BD上,且满足BE=BD,延长AE交BC于点F,则的值为________.13.解析:如图,过D作DG∥AF,交BC于G.在△BDG中,DG∥AF且BE=BD,则BF=FG,5同理,CG=FC.即CG=FG.∴BF=FC.即=.答案:14.已知:如图所示,四边形ABCD是正方形,延长BC到点E,连接AE交CD于点F,FG∥AD交DE于点G.求证:FC=FG.14.证明:在正方形ABCD中, AB∥CD,∴=. FG∥AD,∴=.∴=. AB=AD,∴CF=FG.15.如图所示,在▱ABCD中,点E是AB延长线上一点,DE交AC于点G,交BC于点F.(1)求证:DG2=GE·GF;(2)求证:=.15.证明:(1) CD∥AE,∴=.又 AD∥CF,∴=,∴=,即DG2=GE·GF.(2) BF∥AD,∴=.又 CD∥BE,∴=,∴=.点评:利用定理或其推论解决问题时,要注意寻找图形中的基本图形“A”型或“X”型.16.如图所示,AC∥BD,AD、BC相交于点E,EF∥BD,求证:+=.16.证明: AC∥EF∥BD,∴=,=.两式相加得:+===1,即+=.61.定理应用注意事项.(1)定理的条件:与平行线等分线段定理相同,它需要a、b、c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a、b、c相交,即被平行线a、b、c所截,平行线的条数还可以更多.(2)定理比例的变式:对于3条平行线截两条直线的图形,需要注意以下变化:如果已知a∥b∥c,那么根据定理就可以得到所有的对应线段都成比例,可以归纳为=,=,=等,便于记忆.2.解题思路.(1)利用平行线分线段成比例定理及其推论,要注意线段的对应关系,有时要用到比例的一些性质才能解决相关问题,过定点作某一线段的平行线是常用的作辅助线的方法.(2)“平行线”在解决比例问题时有很重要的作用,如题目中有平行线,要充分利用这一条件,若没有平行关系,需构造一组平行线,利用平行关系,找出对应的比例关系.【习题1.2】1.解析:如图所示,由题意知△OCD∽△OAB,∴△OCD与△OAB的三边对应成比例.∴=....