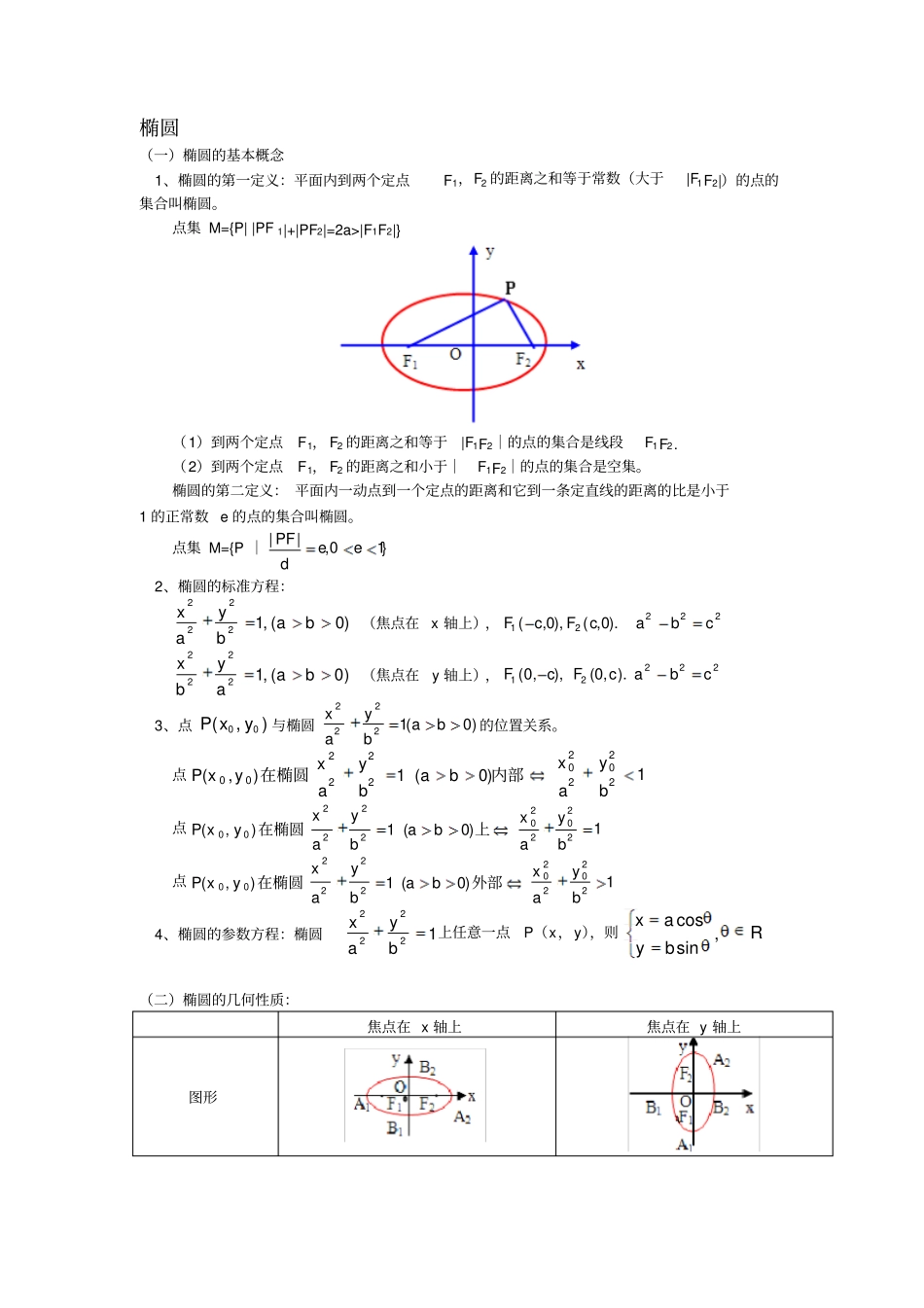
椭圆(一)椭圆的基本概念1、椭圆的第一定义:平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的集合叫椭圆。点集M={P||PF1|+|PF2|=2a>|F1F2|}(1)到两个定点F1,F2的距离之和等于|F1F2|的点的集合是线段F1F2.(2)到两个定点F1,F2的距离之和小于|F1F2|的点的集合是空集。椭圆的第二定义:平面内一动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数e的点的集合叫椭圆。点集M={P|}1e0,ed|PF|2、椭圆的标准方程:)0(,12222babyax(焦点在x轴上),22221cba).0,c(F),0,c(F)0(,12222baaybx(焦点在y轴上),22221cba).c,0(F),c,0(F3、点),(00yxP与椭圆)0ba(1byax2222的位置关系。点1byax)0ba(1byax)y,x(P220220222200内部在椭圆点1byax)0ba(1byax)y,x(P220220222200上在椭圆点1byax)0ba(1byax)y,x(P220220222200外部在椭圆4、椭圆的参数方程:椭圆12222byax上任意一点P(x,y),则Rbyax,sincos(二)椭圆的几何性质:焦点在x轴上焦点在y轴上图形性质范围|x|≤a,|y|≤b|x|≤b,|y|≤a对称性关于x轴、y轴、坐标原点对称顶点A1(-a,0)A2(a,0)B1(0,-b)B2(0,b)A1(0,-a)A2(0,a)B1(-b,0)B2(b,0)离心率离心率e=ac,0b>0)3、椭圆上任意一点P到焦点F的距离的最大值是|PF|=a+c,最小值是|PF|=a-c.4、椭圆上任意一点P到两焦点的距离之积的最大值是a2,此时P点与椭圆的短轴的两端点重合5、注意利用平面几何知识解决椭圆问题。如:|PN||PM||PF||PF|,|OA||OF||PN||PF||PM||PF|212221双曲线1.双曲线定义:第一定义:平面内到两定点21,FF距离之差的绝对值等于常数(小于||21FF)的点的集合叫做双曲线。定点21,FF叫双曲线的焦点,两焦点间距离是焦距。M=|}FF|a2,a2||PF||PF|||P{2121第二定义:平面内到定点F的距离与到定直线L的距离之比是大于1的常数的点的集合叫双曲线,定点是双曲线的焦点,定直线是双曲线的准线。M=}1,|||{eedPFP注意:(1)在第一定义中:若2a=||21FF,则点的集合是以21,FF为端点的射线,若2a>||21FF,点的集合是空集。(2)在第一定义中:当aPFPF2||||21,则点的集合是双曲线的右支(如图1),当aPFPF2||||12,点的集合是双曲线的左支(如图2)。(3)在定义二中定点F不在定直线L上。2.双曲线的标准方程(1))0,0(,12222babyax,焦点在x轴上(实轴在x轴上),222cba(2))0,0(,12222babxay,焦点在y轴上(实轴在y轴上),222cba3.双曲线几何性质图形对称性关于x轴、y轴、原点对称范围ax或axay或ay顶点A1(-a,0)A2(a,0)实轴:2a,虚轴:2bA1(0,-a)A2(0,a)实轴:2a虚轴:2b离心率1ace(e:确定双曲线的开口程度)渐近线xabyxbay焦点半径(1)P(),00yx点在右支上,则01||exaPF,02||exaPF(2)P),(00yx点在左支上,则aexPFaexPF0201||,||(1)),(00yxP点在上支上0201||,||eyaPFeyaPF(2)P),(00yx点在下支上aeyPFaeyPF0201||||,4.求双曲线标准方程常见的类型及方法:(1)定义法(已知条件满足双曲线定义)(2)待定系数法(定位:确定双曲线的焦点位置,设方程:根据焦点位置设方程,定值:确定系数)(3)已知渐进线方程0aybx,可设双曲线方程是2222yaxb,确定值即可。(4)不能确定双曲线的焦点位置时。可设方程为:)0(,122mnnymx(5)与双曲线)0,0(,12222babyax共焦点的双曲线方程设为:)(,1222222akbkbykax5.几种特殊的双曲线(1)等轴双曲线:222ayx,(等轴双曲线离心率是2)(2)共扼双曲线:1122222222byaxbyax与互为共轭双曲线。(性质:(1)互为共轭双曲线的四个焦点共圆,(2)离心率倒数平方和等于1,(3)有相同的渐近线)6.双曲线中的基本三角形:(1)如图3:,tan,||,||,|OA|abAOBbABcOBaAOB中,AOBecos1(2)焦点三角形21PFF的面积:2cot2bS,(21PFF)抛...