第6章 平面问题高阶单元VIP免费

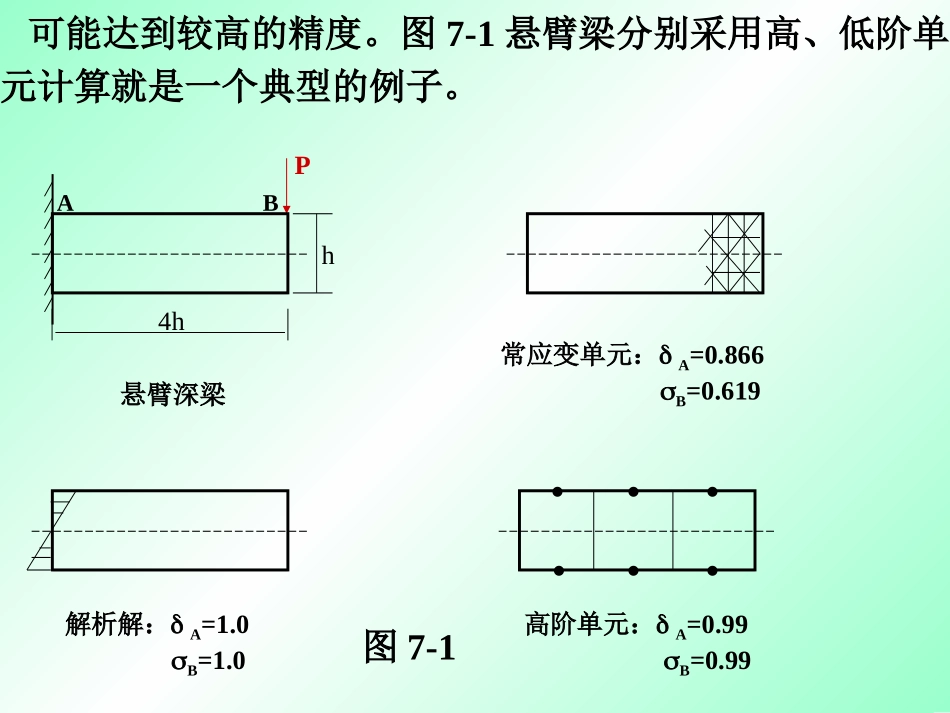
第7章平面问题高阶单元7.1位移模式阶次的选择在前面两章中讨论了平面问题三结点三角形单元，其位移模式的最高阶是坐标x、y的一次项。这种位移模式导致单元常应变、常应力特性，单元应变矩阵、应力矩阵、刚度矩阵均为常数矩阵，因此计算非常简单。但这种单元难以反映应力梯度的迅速变化。要想提高计算精度，必须细分网格，增加单元数和点数，因而加大输入数据的工作量。提高计算精度的另一条有效途径是采用高阶单元。由于高阶单元的应变、应力不再是常数，因此采用少量单元就可能达到较高的精度。图7-1悬臂梁分别采用高、低阶单元计算就是一个典型的例子。h4hPAB悬臂深梁解析解：A=1.0B=1.0常应变单元：A=0.866B=0.619高阶单元：A=0.99B=0.99••••••图7-1选择位移模式时，第2章提到要考虑解的收敛性，即要考虑到位移模式的完备性和协调性。实际操作中，一般应考虑位移模式的对称性。这是因为，有限元位移模式的选择实际是以帕斯卡（Pascal）三解形基础上的（如图7-2所示），由低价至高阶，顺序选取，组成多项式。多项式中的项数等于单元节点自由度数。如三节点三角形单元，位移模式取完全一次式，共3项。六节点三角形单元，位移模式取完全二次式共6项。如果某一阶次不能全取，则应按对称性原则适当选取。1xyx2xyy2x3x2yxy2y3x4x3yx2y2xy3y4图7-2多项式选择的怕斯卡三角形1xyx2xyy2x3x2yxy2y3x4x3yx2y2xy3y4图7-2多项式选择的怕斯卡三角形例如在下节将要讨论的四结点矩形单元中，位移模式不能取1，x，y，x2四项，也不能取1，x，y，y2四项，而应取1，x，y，xy四项。7.2四节点矩形单元图7-3示出的矩形单元，边长分别为2a和2b。取4个角点为节点，编号为i，j，l，m。将x轴和y轴置于单元的对称轴上。单元的位移函数可取为：1、位移函数在上式表示的位移模式中，a1,a2,a3,a5,a6,a7，a8反映了单元的刚体位移和常应变。在单元的边界(x=±a或y=±a)上（或），位移是按线性分布的。因此，相邻单元在公共边上的位移是连续的。这样，位移模式满足了解答收敛性的充分条件。ijlmxyaabb图7-3在式（7-1）中代入节点位移和节点坐标后，可解出xyayaxaavxyayaxaau87654321（7-1）式中形函数为：byaxNbyaxNbyaxNbyaxNmlji1141114111411141（7-3）mmlljjiimmlljjiiuNuNuNuNvuNuNuNuNu（7-2）各待定系数(a1…a8)。将这些系数再代入式（7-1），可得：则式（7-3）可简写为),,,(4/)1)(1(mljiNiii（7-4）将位移函数写成矩阵形式，即有与式（2-20）相同的形式eNvuf}]{[}{（7-5）式中Tmmlljjiievuvuvuvu][}{（7-6）令byax,在节点上的值为：),,,(,mljibyaxiiii][][ININININNnlji（7-7）其中，I为二阶单位矩阵。2、应变矩阵根据几何方程，可得与式（2-25）同样的形式eB}]{[}{（7-8）把应变矩阵[B]写成子矩阵形式]][][][][[][mljiBBBBB（7-9）其中),,,()1()1()1(00)1(41][mljibaababBiiiiiiiii（7-10）由此可见，[B]是、的函数，即是x、y的函数。因此单元中的应变不再是常数。3、应力矩阵根据应力-应变关系，可以计算单元中的应力，得到式（2-28）同样形式eSD]][[}]{[}{（7-11）应力矩阵[S]具有与式（2-29）同样形式]][[][BDS（7-12）将[S]写成子矩阵形式（7-13）][][mljiSSSSS其中)1(21)1(21)1()1()1()1()1(4][2iiiiiiiiiiiiibaabababES),,,(mlji（7-14）上式对应平面应力情形。对于平面应变情形，只需将其中的E，作相应的改变即可。4、单元刚度矩阵单元刚度矩阵可采用式（2-33a）进行计算AThdxdyBDBk]][[][][（2-33a）在四节点矩形单元中，[k]是一个8×8的矩阵。将[k]写成分块形式：][][][][][][][][][][][][][][...