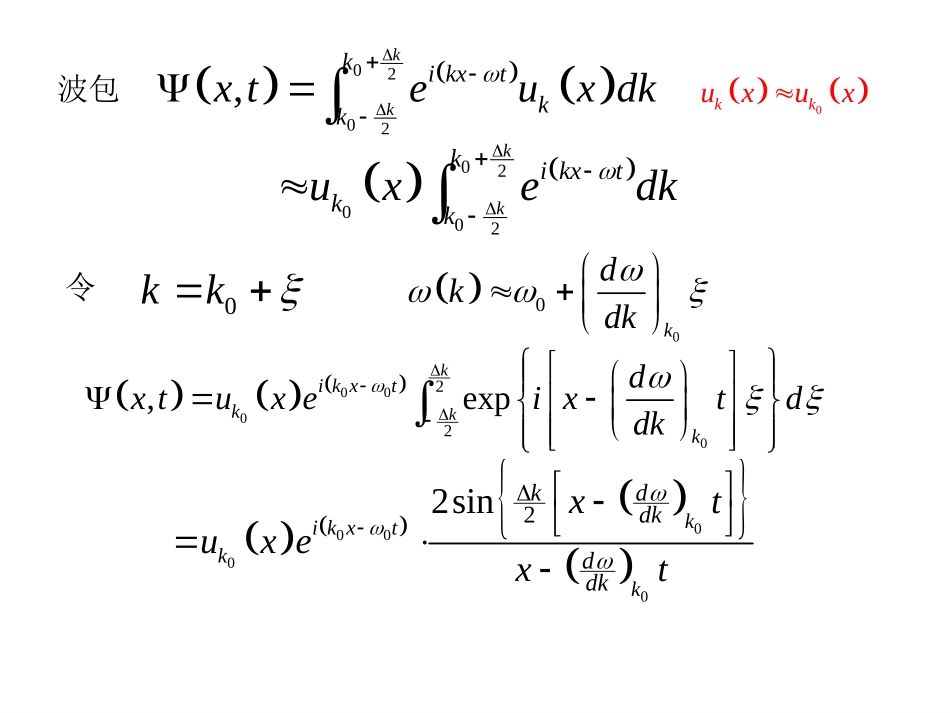第七章 晶体中电子在电场和磁场中的运动VIP免费

第七章晶体中电子在电场和磁场中的运动由于通常外加的场总是比晶体的周期场弱得多，因而可以在周期场的本征态的基础上进行讨论。采用的方法有两种：一是解含外场的波动方程222UVEmr通常情况下，这只能得到近似解；另一种方法是在一定条件下，把晶体中电子在外场中的运动当作准经典粒子来处理。条件：外场较弱、恒定，不考虑电子在不同能带间的跃迁，不考虑电子的衍射、干涉及碰撞等。§7.1准经典运动一、波包与电子速度在晶体中，可以用Bloch函数来组成波包。由于波包中含有能量不同的本征态，因此，必须用含时间的Bloch函数。对于一维情况，设波包由以k0为中心，在k的范围内的波函数组成，并假设k很小，可近似认为0kkuxux不随k而变。对于一确定的k，含时的Bloch函数为,ikxtkkxteux/kEk波包0202,kkkikxtkkxteuxdk02002kkkikxtkkuxedk令0kk00kdkdk000022,expkkikxtkkdxtuxeixtddk0000022sinkikxtkkkddkddkxtuxext0kkuxux为分析波包的运动，只需分析2，即几率分布即可。000222222sin,kkkkddkkddkxtxtuxkxt令0kdwxtdkw2k2k0222sinkkww波函数集中在尺度为的范围内，波包中心为：w＝0。2k有001kkddExttdkdk若将波包看成一个准粒子，则粒子的速度为001kdxdEvkdtdkEkk布里渊区的宽度：2/a，而假设k很小，一般要求2ka即2ak推广到三维情况，电子速度为1Ekv电子速度的方向为k空间中能量梯度的方向，即垂直于等能面。因此，电子的运动方向决定于等能面的形状，在一般情况下，在k空间中，等能面并不是球面，因此，v的方向一般并不是k的方向，只有当等能面为球面，或在某些特殊方向上，v才与k的方向相同。电子运动速度的大小与k的关系，以一维为例。在能带底和能带顶，E(k)取0dEdk极值，。因此，在能带底和能带顶，电子速度v＝0。220dEdk而在能带中的某处，电子速度的数值最大，这种情况与自由电子的速度总是随能量的增加而单调上升是完全不同的。二、电子的准动量在外场中，电子所受的力为F，在dt时间内，外场对电子所做的功为Fvdt根据功能原理，有dtdEEdkFvk1Ekv0ddtkFv在平行于v的方向上，和F的分量相等；当F与速度v垂直时，不能用功能原理来讨论电子能量状态的变化，但是我们仍可以证明在垂直于速度的方向上，ddtkddtk和外力F的分量也相等。ddtkF上式是电子在外场作用下运动状态变化的基本公式，具有与经典力学中牛顿定律相似的形式。k——电子的准动量。三、电子的加速度和有效质量晶体中电子准经典运动的基本关系式：1EddtkvkF{由以上两式可直接导出在外力作用下电子的加速度。1.一维情况2222211dEdkdvddEdkdEFadtdtdkdtdk引入电子的有效质量：222dEdkmdvFmdt有由于周期场中电子的能量E(k)与k的函数关系不是抛物线关系，因此，电子的有效质量m*与k有关。在能带底，220dEdkE(k)取极小值，这时，m*>0；在能带顶，E(k)取极大值，220dEdk所以，m*<0。2.三维情况11dddEEdtdtdtkkkvka其分量形式为3111dkdvdEEadtdtkdtkk23211EFkk＝1,2,3矩阵形式22222222222221xxyxzxxyyyxyyzzzzxzyzEEEkkkkkvFEEEvFkkkkkvFEEEkkkkk与牛顿定律1mvF相比可知...