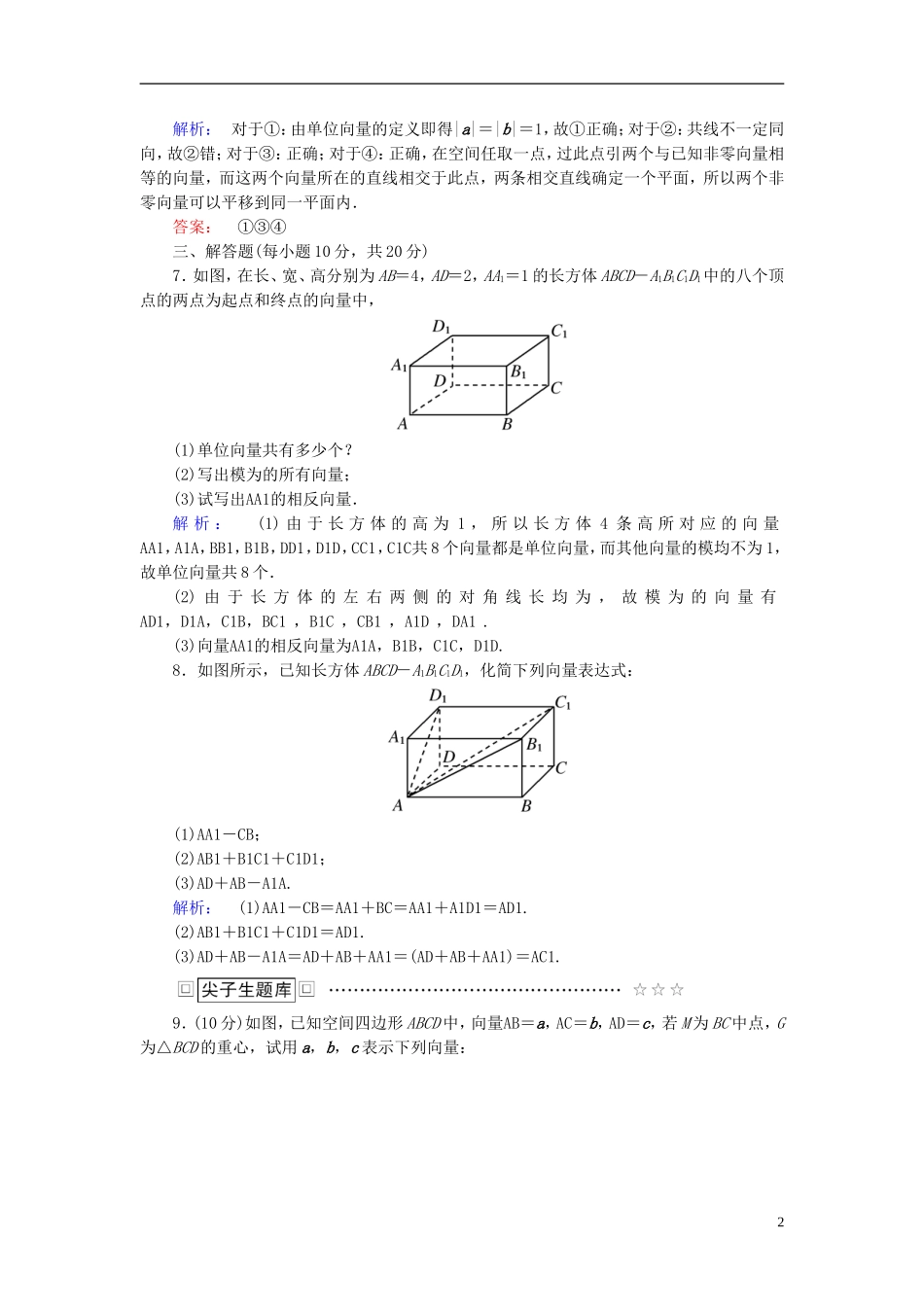
2016-2017学年高中数学第三章空间向量与立体几何3.1.1空间向量及其加减运算高效测评新人教A版选修2-1一、选择题(每小题5分,共20分)1.在平行六面体ABCD-A′B′C′D′中,与向量A′B′的模相等的向量有()A.7个B.3个C.5个D.6个解析:|D′C′|=|DC|=|C′D′|=|CD|=|BA|=|AB|=|B′A′|=|A′B′|.答案:A2.已知向量a,b是两个非零向量,a0,b0是与a,b同方向的单位向量,那么下列各式中正确的是()A.a0=b0B.a0=b0或a0=-b0C.a0=1D.|a0|=|b0|解析:两单位向量的模都是1,但方向不一定相同或相反.答案:D3.下列命题是真命题的是()A.分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量B.若|a|=|b|,则a,b的长度相等而方向相同或相反C.若向量AB,CD满足|AB|>|CD|,且AB与CD同向,则AB>CDD.若两个非零向量AB与CD满足AB+CD=0,则AB∥CD解析:A错.因为空间任两向量平移之后可共面,所以空间任两向量均共面.B错.因为|a|=|b|仅表示a与b的模相等,与方向无关.C错.空间任两向量不研究大小关系,因此也就没有AB>CD这种写法.D对.∵AB+CD=0,∴AB=-CD,∴AB与CD共线,故AB∥CD正确.答案:D4.已知向量AB,AC,BC满足|AB|=|AC|+|BC|,则()A.AB=AC+BCB.AB=-AC-BCC.AC与BC同向D.AC与CB同向解析:由|AB|=|AC|+|BC|=|AC|+|CB|,知C点在线段AB上,否则与三角形两边之和大于第三边矛盾,所以AC与CB同向.答案:D二、填空题(每小题5分,共10分)5.如图,在三棱柱ABC-A1B1C1中,CA与C1A1是________向量,CB与B1C1是________向量.解析:CA綊C1A1,CB綊C1B1,所以CA=C1A1,CB=-B1C1.答案:相等相反6.下列命题中正确的是________.①如果a,b是两个单位向量,则|a|=|b|;②两个空间向量共线,则这两个向量方向相同;③若a,b,c为非零向量,且a∥b,b∥c,则a∥c;④空间任意两个非零向量都可以平移到同一平面内.1解析:对于①:由单位向量的定义即得|a|=|b|=1,故①正确;对于②:共线不一定同向,故②错;对于③:正确;对于④:正确,在空间任取一点,过此点引两个与已知非零向量相等的向量,而这两个向量所在的直线相交于此点,两条相交直线确定一个平面,所以两个非零向量可以平移到同一平面内.答案:①③④三、解答题(每小题10分,共20分)7.如图,在长、宽、高分别为AB=4,AD=2,AA1=1的长方体ABCD-A1B1C1D1中的八个顶点的两点为起点和终点的向量中,(1)单位向量共有多少个?(2)写出模为的所有向量;(3)试写出AA1的相反向量.解析:(1)由于长方体的高为1,所以长方体4条高所对应的向量AA1,A1A,BB1,B1B,DD1,D1D,CC1,C1C共8个向量都是单位向量,而其他向量的模均不为1,故单位向量共8个.(2)由于长方体的左右两侧的对角线长均为,故模为的向量有AD1,D1A,C1B,BC1,B1C,CB1,A1D,DA1.(3)向量AA1的相反向量为A1A,B1B,C1C,D1D.8.如图所示,已知长方体ABCD-A1B1C1D1,化简下列向量表达式:(1)AA1-CB;(2)AB1+B1C1+C1D1;(3)AD+AB-A1A.解析:(1)AA1-CB=AA1+BC=AA1+A1D1=AD1.(2)AB1+B1C1+C1D1=AD1.(3)AD+AB-A1A=AD+AB+AA1=(AD+AB+AA1)=AC1.9.(10分)如图,已知空间四边形ABCD中,向量AB=a,AC=b,AD=c,若M为BC中点,G为△BCD的重心,试用a,b,c表示下列向量:2(1)DM;(2)AG.解析:(1)连接AM,在△ADM中,DM=DA+AM,由线段中点的向量表示知,AM=(AB+AC)=(a+b).由相反向量的概念知,DA=-AD=-c.所以DM=DA+AM=(a+b)-c=(a+b-2c).(2)在△ADG中,注意到三角形重心的性质,得AG=AD+DG=c+DM=c+=c+(AB-AD+AC-AD)=c+(a+b-2c)=(a+b+c).3