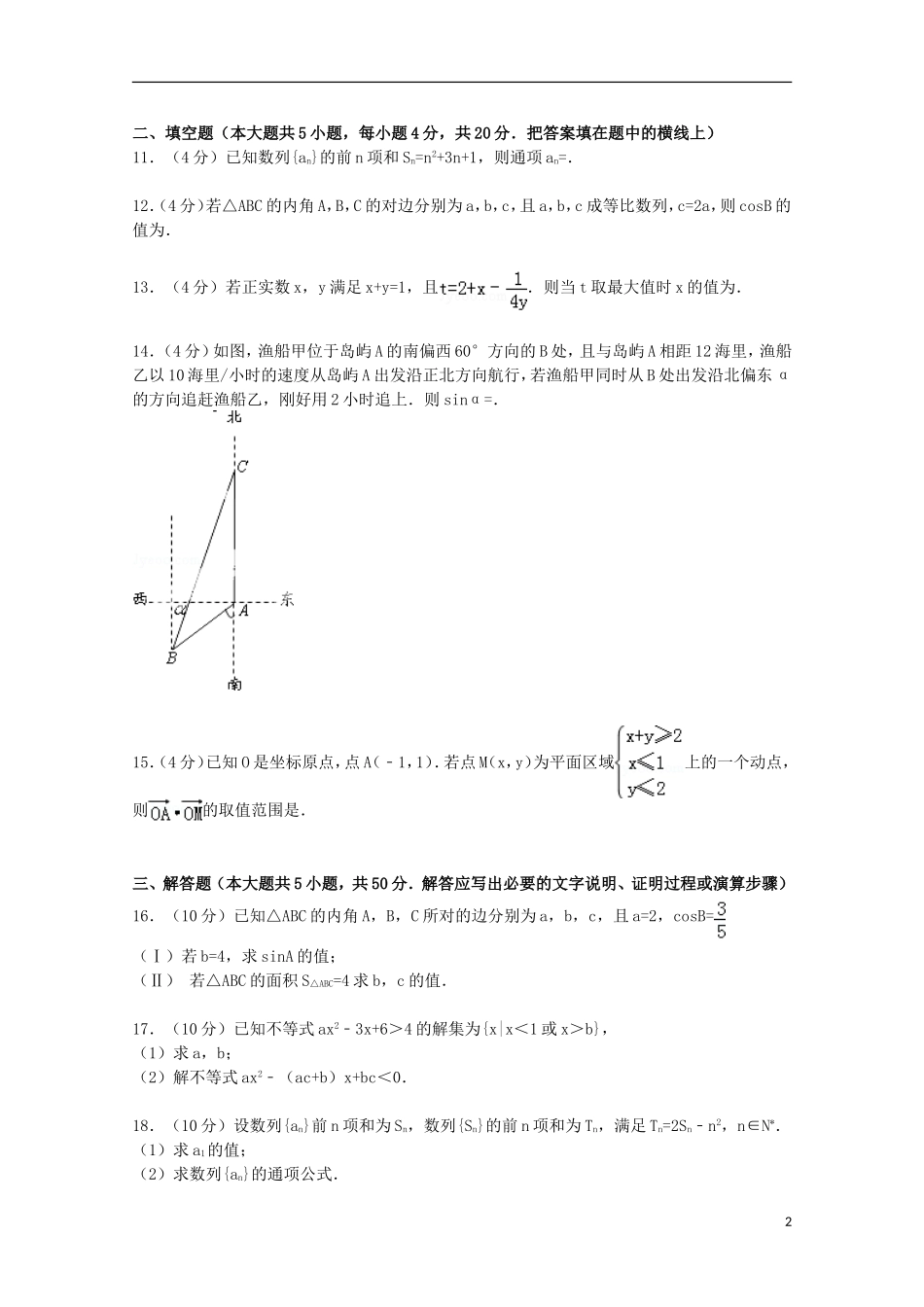
广东省揭阳三中2014-2015学年高二上学期模块数学试卷(必修5)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)若a>b,则下列正确的是()A.a2>b2B.ac>bcC.ac2>bc2D.a﹣c>b﹣c2.(5分)在△ABC中,A=60°,,则∠B等于()A.45°或135°B.135°C.45°D.30°3.(5分)已知数列{an}中,a1=1,an+1=an+3,若an=2014,则n=()A.667B.668C.669D.6724.(5分)若集合M={x|x2>4},,则M∩N=()A.{x|x<﹣2}B.{x|2<x<3}C.{x|x<﹣2或x>3}D.{x|x>3}5.(5分)已知各项均为正数的等比数列{an},a1•a9=16,则a2•a5•a8的值()A.16B.32C.48D.646.(5分)在△ABC中,角A,B,C所对的边分别是a,b,c,若acosB=bcosA,则△ABC是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形7.(5分)若实数x,y满足,则S=2x+y﹣1的最大值为()A.6B.4C.3D.28.(5分)函数f(x)=的最大值为()A.B.C.D.19.(5分)公差不为零的等差数列{an}的前n项和为Sn.若a4是a3与a7的等比中项,S8=32,则S10等于()A.18B.24C.60D.9010.(5分)△ABC中,BC=2,角B=,当△ABC的面积等于时,sinC=()A.B.C.D.1二、填空题(本大题共5小题,每小题4分,共20分.把答案填在题中的横线上)11.(4分)已知数列{an}的前n项和Sn=n2+3n+1,则通项an=.12.(4分)若△ABC的内角A,B,C的对边分别为a,b,c,且a,b,c成等比数列,c=2a,则cosB的值为.13.(4分)若正实数x,y满足x+y=1,且.则当t取最大值时x的值为.14.(4分)如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.则sinα=.15.(4分)已知O是坐标原点,点A(﹣1,1).若点M(x,y)为平面区域上的一个动点,则的取值范围是.三、解答题(本大题共5小题,共50分.解答应写出必要的文字说明、证明过程或演算步骤)16.(10分)已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,cosB=(Ⅰ)若b=4,求sinA的值;(Ⅱ)若△ABC的面积S△ABC=4求b,c的值.17.(10分)已知不等式ax2﹣3x+6>4的解集为{x|x<1或x>b},(1)求a,b;(2)解不等式ax2﹣(ac+b)x+bc<0.18.(10分)设数列{an}前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn﹣n2,n∈N*.(1)求a1的值;(2)求数列{an}的通项公式.219.(10分)为了提高产品的年产量,某企业拟在2013年进行技术改革,经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3﹣(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)(1)试确定k的值,并将2013年该产品的利润y万元表示为技术改革费用m万元的函数(利润=销售金额﹣生产成本﹣技术改革费用);(2)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.20.(10分)定义:若数列{An}满足An+1=An2,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.(1)证明:数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)•…•(2an+1),求数列{an}的通项及Tn的表达式.广东省揭阳三中2014-2015学年高二上学期模块数学试卷(必修5)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)若a>b,则下列正确的是()A.a2>b2B.ac>bcC.ac2>bc2D.a﹣c>b﹣c考点:不等关系与不等式.专题:证明题.分析:由不等式的运算性质对四个选...