历年高考数学真题考点归纳 第四章 三角函数及三角恒等变换 第二节 三角函数的图像和性质及三角恒等变换试卷VIP免费

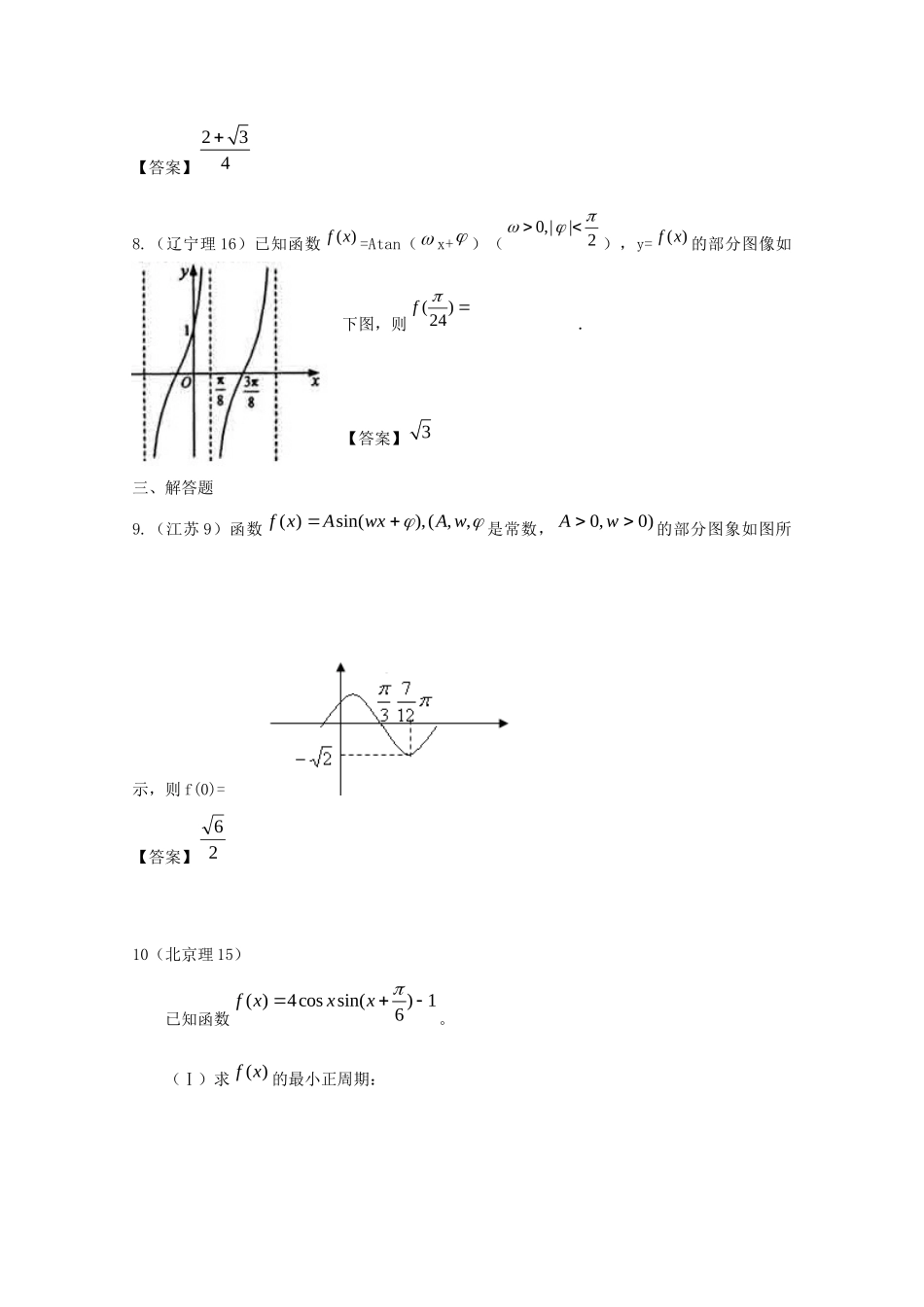
历年高考真题考点归纳2011年第四章三角函数及三角恒等变换第二节三角函数的图像和性质及三角恒等变换一、选择题1.（山东理6）若函数()sinfxx(ω>0)在区间0,3上单调递增，在区间,32上单调递减，则ω=A．3B．2C．32D．23【答案】C2.（山东理9）函数2sin2xyx的图象大致是【答案】C3.（全国大纲理5）设函数()cos(0)fxx＞，将()yfx的图像向右平移3个单位长度后，所得的图像与原图像重合，则的最小值等于A．13B．3C．6D．9【答案】C4.（湖北理3）已知函数()3sincos,fxxxxR，若()1fx，则x的取值范围为A．|,3xkxkkZB．|22,3xkxkkZC．5{|,}66xkxkkZD．5{|22,}66xkxkkZ【答案】B5.（全国新课标理11）设函数()sin()cos()fxxx(0,||)2的最小正周期为，且()()fxfx则（A）()yfx在(0,)2单调递减（B）()yfx在3(,)44单调递减（C）()yfx在(0,)2单调递增（D）()yfx在3(,)44单调递增【答案】A6.（安徽理9）已知函数()sin(2)fxx，其中为实数，若()()6fxf对xR恒成立，且()()2ff，则()fx的单调递增区间是（A）,()36kkkZ（B）,()2kkkZ（C）2,()63kkkZ（D）,()2kkkZ【答案】C二、填空题7.（上海理8）函数sin()cos()26yxx的最大值为。【答案】2348.（辽宁理16）已知函数)(xf=Atan（x+）（2||,0），y=)(xf的部分图像如下图，则)24(f．【答案】3三、解答题9.（江苏9）函数,,(),sin()(wAwxAxf是常数，)0,0wA的部分图象如图所示，则f(0)=【答案】2610（北京理15）已知函数()4cossin()16fxxx。（Ⅰ）求()fx的最小正周期：（Ⅱ）求()fx在区间,64上的最大值和最小值。解：（Ⅰ）因为1)6sin(cos4)(xxxf1)cos21sin23(cos4xxx1cos22sin32xxxx2cos2sin3)62sin(2x所以)(xf的最小正周期为（Ⅱ）因为.32626,46xx所以于是，当6,262xx即时，)(xf取得最大值2；当)(,6,662xfxx时即取得最小值—1.11．（福建理16）已知等比数列{an}的公比q=3，前3项和S3=133。（I）求数列{an}的通项公式；（II）若函数()sin(2)(0,0)fxAxAp在6x处取得最大值，且最大值为a3，求函数f（x）的解析式。本小题主要考查等比数列、三角函数等基础知识，考查运算求解能力，考查函数与方程思想，满分13分。解：（I）由313(13)13133,,3133aqS得解得11.3a所以12133.3nnna（II）由（I）可知233,3.nnaa所以因为函数()fx的最大值为3，所以A=3。因为当6x时()fx取得最大值，所以sin(2)1.6又0,.6故所以函数()fx的解析式为()3sin(2)6fxx12.（广东理16）已知函数1()2sin(),.36fxxxR（1）求5()4f的值；（2）设106,0,,(3),(32),22135faf求cos()的值．解：（1）515()2sin()4346f2sin24；（2）10132sin32sin,132326f61(32)2sin(32)2sin2cos,5362f53sin,cos,13522512cos1sin1,13132234sin1cos1,55故3125456cos()coscossinsin.5131356513.（湖北理16）设ABC的内角A、B、C、所对的边分别为a、b、c，已知11.2.cos.4abC（Ⅰ）求ABC的周长（Ⅱ）求cosAC的值本小题主要考查三角函数的基本公式和解斜三角形的基础知识，同时考查基本运算能力。（满分10分）解：（Ⅰ）22212cos14444cababC2.cABC的周长为1225.abc（Ⅱ）22...