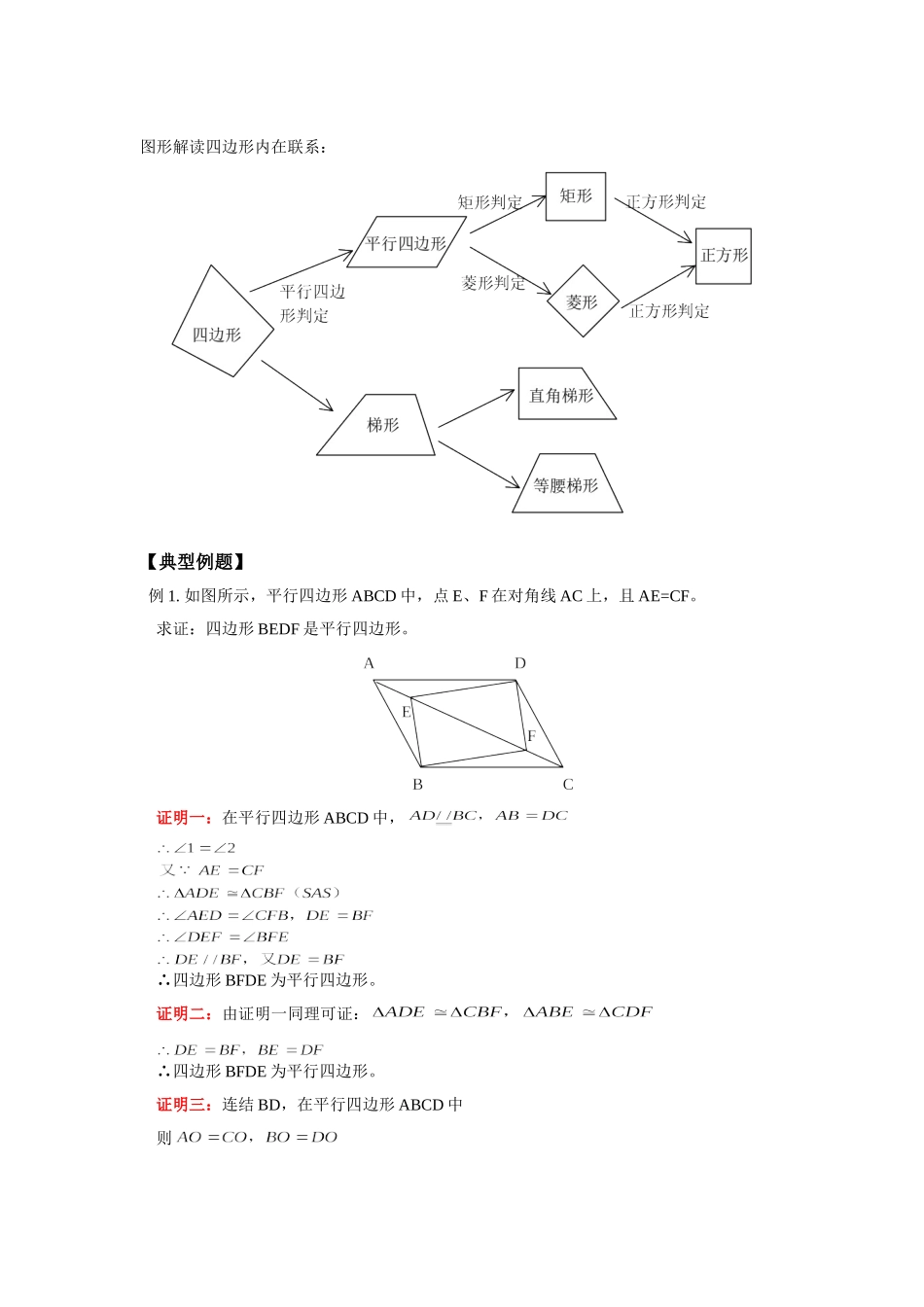
初三数学用推理方法研究四边形华东师大版【同步教育信息】一.本周教学内容:用推理方法研究四边形[重要知识归纳]一.平行四边形1.平行四边形的判定定理:(1)从边的关系去判定①一组对边平行且相等的四边形是平行四边形。②两组对边分别平行的四边形是平行四边形。③两组对边分别相等的四边形是平行四边形。(2)从角的关系去判定④两组对角分别相等的四边形是平行四边形。(注:邻角都互补的四边形也可证其是平行四边形。)(3)从对角线的关系去判定:⑤对角线相互平分的四边形是平行四边形。2.平行四边形的性质定理:(1)从边的关系分析①平行四边形对边平行且相等。(2)从角的关系分析②平行四边形对角相等、邻角互补。(3)从对角线分析③平行四边形对角线互相平分。(4)从对称性分析④平行四边形是中心对称图形,对角线交点是对称中心。(注:由中心对称性,可通过绕三角形一边中点旋转180°来构造平行四边形。)二.矩形1.矩形的判定定理:(1)有一个角是直角的平行四边形是矩形。(2)有三个角是直角的四边形是矩形。(3)对角线相等的平行四边形是矩形。(4)对角线相等且相互平分的四边形是矩形。2.矩形的性质定理:(1)矩形的四个角都是直角。(2)矩形的对角线相等且相互平分。3.矩形的对称性:矩形既是轴对称图形,又是中心对称图形。三.菱形1.菱形的判定定理:①四条边都相等的四边形是菱形。②有一组邻边相等的平行四边形是菱形。③对角线互相垂直的平行四边形是菱形。④对角线互相垂直且平分的四边形是菱形。2.菱形的性质定理:①菱形四条边都相等。②菱形对角线互相垂直且平分,并且每条对角线平分一组对角。3.菱形的对称性:菱形既是轴对称图形又是中心对称图形。4.菱形的面积等于它的两条对角线的乘积的一半。四.正方形1.正方形的性质:(1)正方形四个角都是直角,四条边都相等。(2)正方形两对角线互相垂直平分且相等,并且每条对角线平分一组对角。2.正方形的对称性:正方形既是中心对称图形,又是轴对称图形。3.正方形的边长与对角线长的比为。4.正方形的判定定理:(1)有一组邻边相等的矩形是正方形。(2)对角线相互垂直的矩形是正方形。(3)有一个角是直角的菱形是正方形。(4)对角线相等的菱形是正方形。(5)对角线互相垂直平分且相等的四边形是正方形。注:证明四边形是正方形往往先证明它是矩形或菱形,然后再证明其是正方形,有时也从对角线关系出发直接证其是正方形。图形解读四边形内在联系:【典型例题】例1.如图所示,平行四边形ABCD中,点E、F在对角线AC上,且AE=CF。求证:四边形BEDF是平行四边形。证明一:在平行四边形ABCD中,∴四边形BFDE为平行四边形。证明二:由证明一同理可证:∴四边形BFDE为平行四边形。证明三:连结BD,在平行四边形ABCD中则∴四边形BFDE为平行四边形。例2.分别以平行四边形ABCD的邻边AB和AD为一边,在平行四边形ABCD外作正三角形ABF和正三角形ADE,连结CE、EF、CF得△CEF,试判断△CEF的形状,并证明你的结论。证明: 四边形ABCD是平行四边形 △ADE、△ABF为正三角形例3.已知:如图所示,延长平行四边形ABCE的边BC至E,DA至F,使CE=AF,EF与BD交于点O,求证:EF与BD互相平分。证明:连结FB,DE 四边形ABCD是平行四边形∴四边形FBED是平行四边形∴EF与BD互相平分。例4.已知:如图所示,在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E。求证:△ACE是等腰三角形。证法一:∴四边形BDCE是_____________四边形。∴BD=EC 四边形ABCD是矩形∴AC=_____________。∴AC=EC,∴△ACE是等腰三角形证法二: 四边形ABCD是矩形∴四边形BDCE是平行四边形∴EB=CD∴AB=EB在△ABC和△EBC中即△ACE是等腰三角形。证法三: 四边形ABCD是矩形∴△ACE为等腰三角形。例5.如图所示,延长矩形的边CB至E,使CE=CA,F是AE的中点,求证:。证明: 四边形ABCD是矩形 F是AE的中点(直角三角形斜边中线等于___________)。_________。即在△ADF和△BCF中例6.已知:如图所示,将矩形ABCD沿着直线BD折叠,使点C落在C’处,BC’交AD于E,AD=8,AB=4,求△BED的面积。解:在矩形ABCD中,AD//BC,当矩形AB...