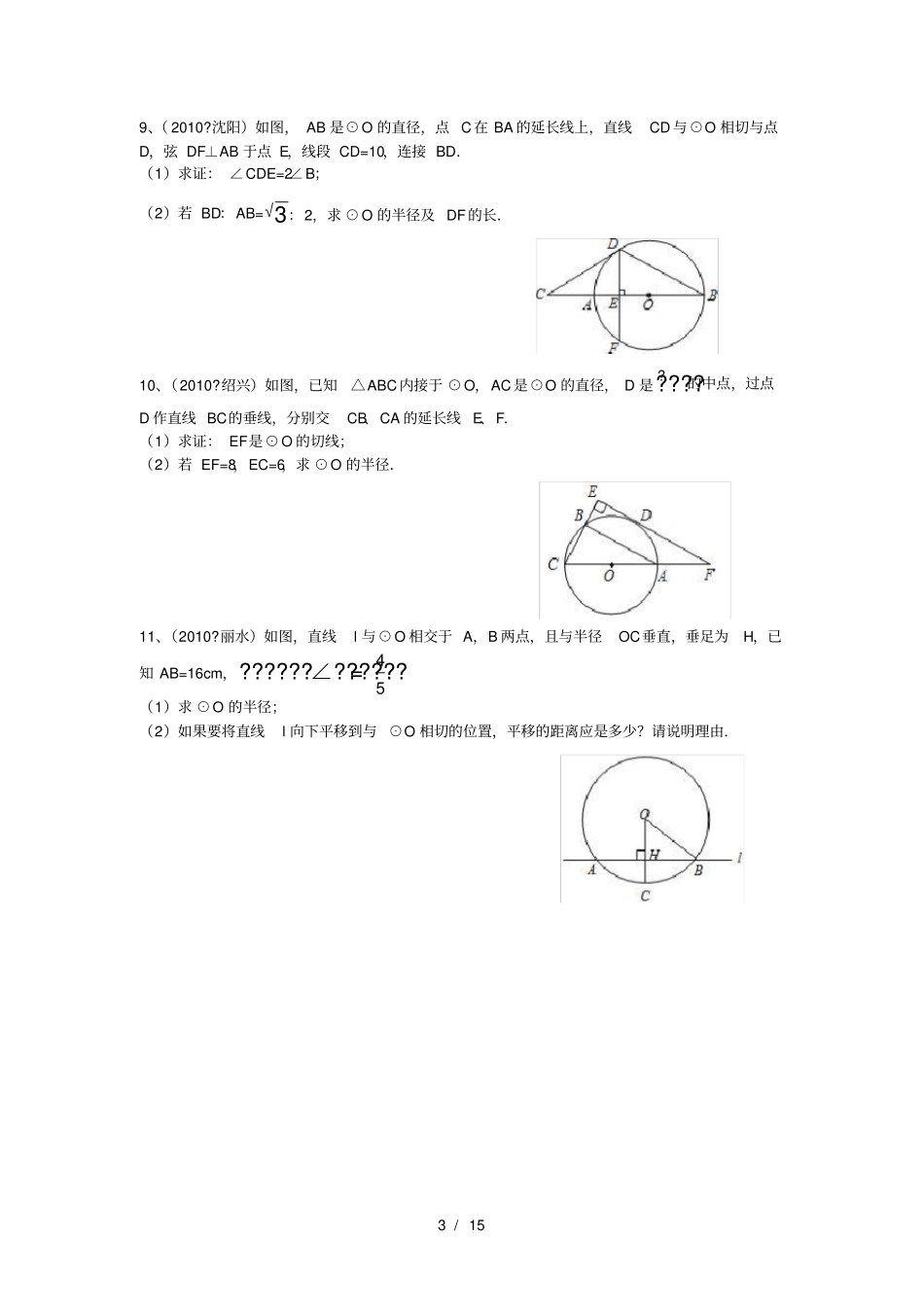
1/151、(2011?湖州)如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;(2)求图中阴影部队的面积.2、(2011?衡阳)如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.(1)判断CD与⊙O的位置关系并说明理由;(2)若∠ACB=120°,OA=2.求CD的长.3、(2011?杭州)在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形(1)你取出的是哪个三角形?写出平移的方向和平移的距离;(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于52?请说明理由.4、(2011?杭州)在△ABC中,AB=√3,AC=√2,BC=1.(1)求证:∠A≠30°;(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.2/155、(2011?贵阳)在?ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.(1)圆心O到CD的距离是_________.(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)6、(2011?抚顺)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.(1)求证:CF为⊙O的切线.(2)若半径ON⊥AD于点M,CE=√3,求图中阴影部分的面积.7、(2011?北京)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=12∠CAB.(1)求证:直线BF是⊙O的切线;(2)若AB=5,sin∠CBF=√55,求BC和BF的长.8、(2010?义乌市)如图,以线段AB为直径的⊙O交线段AC于点E,点M是?????的中点,OM交AC于点D,∠BOE=60°,cosC=12,BC=2√3.(1)求∠A的度数;(2)求证:BC是⊙O的切线(3)求MD的长度.3/159、(2010?沈阳)如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切与点D,弦DF⊥AB于点E,线段CD=10,连接BD.(1)求证:∠CDE=2∠B;(2)若BD:AB=√3:2,求⊙O的半径及DF的长.10、(2010?绍兴)如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是?????的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F.(1)求证:EF是⊙O的切线;(2)若EF=8,EC=6,求⊙O的半径.11、(2010?丽水)如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16cm,??????∠??????=45.(1)求⊙O的半径;(2)如果要将直线l向下平移到与⊙O相切的位置,平移的距离应是多少?请说明理由.4/151、(2011?湖州)如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;(2)求图中阴影部队的面积.考点:扇形面积的计算;垂径定理。分析:(1)在△OCE中,利用三角函数即可求得CE,OE的长,再根据垂径定理即可求得CD的长;(2)根据半圆的面积减去△ABC的面积,即可求解.解答:解:(1)在△OCE中, ∠CEO=90°,∠EOC=60°,OC=2,∴OE=12OC=1,∴CE=√32OC=√3, OA⊥CD,∴CE=DE,∴CD=2√3;(2) S△ABC=12AB?EC=12×4×√3=2√3,∴??阴影=12??×22﹣2√3=2??﹣2√3.点评:本题主要考查了垂径定理以及三角函数,一些不规则的图形的面积可以转化为规则图形的面积的和或差求解.2、(2011?衡阳)如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.(1)判断CD与⊙O的位置关系并说明理由;(2)若∠ACB=120°,OA=2.求CD的长.考点:切线的判定与性质;勾股定理;垂径定理;圆周角定理。专题:综合题。分析:(1)连接OC,证明OC⊥DC,利用经过半径的外端且垂直于半径的直线是圆的切线判5/15定切线即可;(2)利用等弧所对的圆心角相等和题目中的已知角得到∠D=30°,利用解直角三角形求得CD的长即可.解答:解:(1)CD与⊙O相切;证明:连接OC, CA=CB,∴?????=?????∴OC⊥AB, CD∥AB,∴OC⊥CD, OC是半径,∴CD与⊙O相切.(2) CA=CB,∠ACB=120°,∴∠DOC=60°∴∠D=30°, OA=2,∴OC=2∴CD=√????2﹣????2=2√3点评:本题考查常见的几何题型,包括切线的判定,角的大小及线段长度的求法,要求学生掌握常见的解题方法,并能结合图...