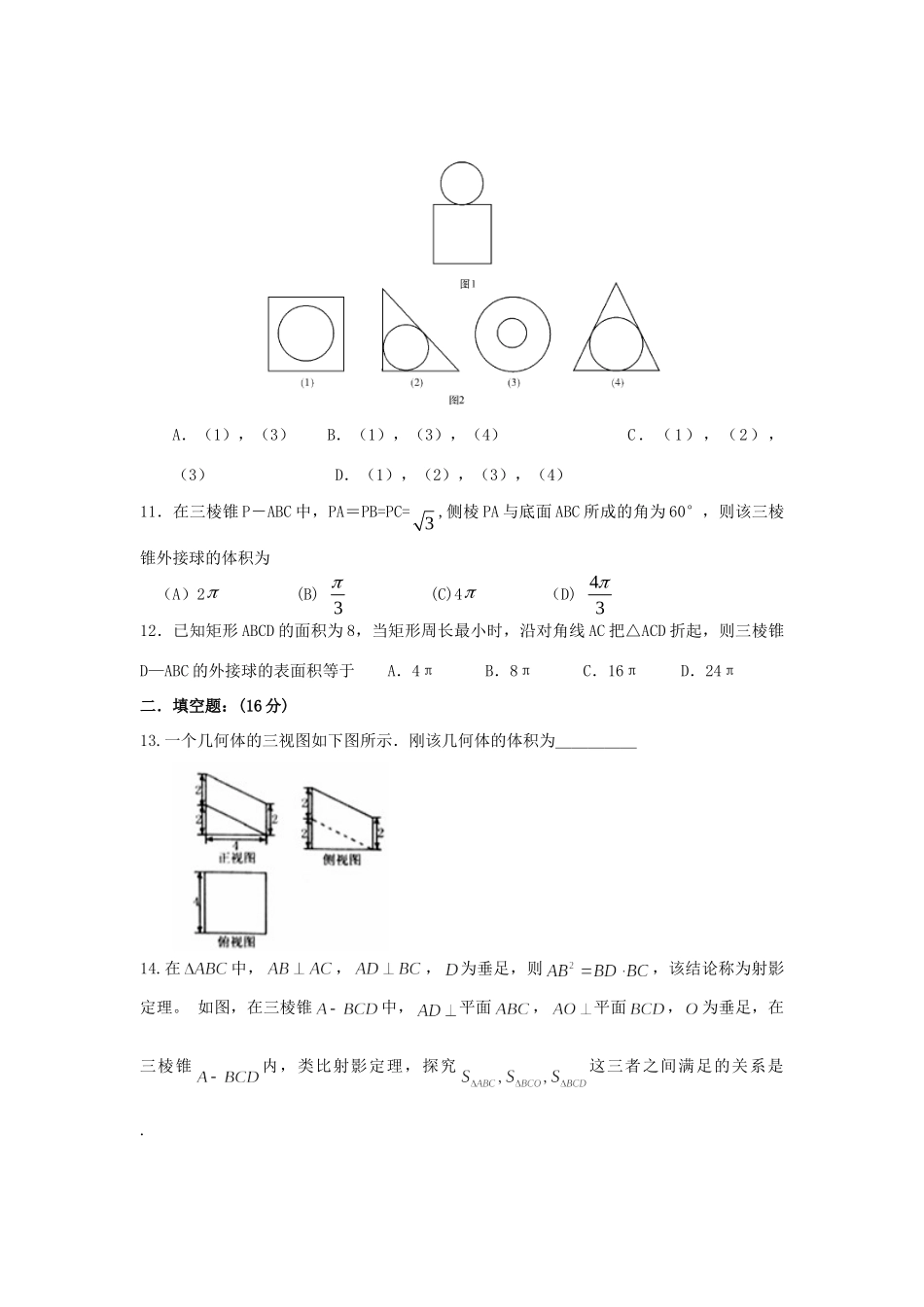
望子成龙学校高二上数学半期摸拟题一.选择题:(60分)1.在空间,异面直线a,b所成的角为α,且=A.B.C.或D.2.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以是()[学7优5高0考g网kGkStK]3.已知三条不重合的直线,两个不重合的平面,有下列命题:①若∥,,则∥;②若,,且∥,则∥③若,,,∥,则∥④若,=,,,则,其中正确命题的个数为()A.1个B.2个C.3个D.4个4.如右图是某几何体的三视图,则该几何体的体积为()A、16B、24C、34D、485.在空间中.l、m、n是三条不同的直线,α、β、γ是三个不同的平面,则下列结论错误的是:A.若α∥β,α∥γ,则β∥γB.若l∥α,l∥β,α∩β=m,则l∥mC.α⊥β,α⊥γ,β∩γ=l,则l⊥αD.若α∩β=m,β∩γ=l,γ∩α=n,l⊥m,l⊥n,则m⊥n(正视图)(俯视图)(A)(B)(C)(D)6.空间几何体的三视图如图所示,则该几何体的表面积为(A)6+25(B)8+23(C)8+25(B)6+237.已知平面内不共线的四点O,A,B,C满足则()A.1:3B.2:1C.1:2D.3:18.已知底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥的主视图、俯视图如图所示,其中为棱CB的中点,则该三棱锥的左视图的面积为()A.9B6.C.D.9.在三棱锥中,若O是底面ABC内部一点,满足,则()A.B.5C.2D.10.某几何体的正视图和侧视图均为如图1所示,则在图2的四个图中可以作为该几何体的俯视图的是A.(1),(3)B.(1),(3),(4)C.(1),(2),(3)D.(1),(2),(3),(4)11.在三棱锥P-ABC中,PA=PB=PC=3,侧棱PA与底面ABC所成的角为60°,则该三棱锥外接球的体积为(A)2(B)3(C)4(D)4312.已知矩形ABCD的面积为8,当矩形周长最小时,沿对角线AC把△ACD折起,则三棱锥D—ABC的外接球的表面积等于A.4πB.8πC.16πD.24π二.填空题:(16分)13.一个几何体的三视图如下图所示.刚该几何体的体积为_____14.在中,,,为垂足,则,该结论称为射影定理。如图,在三棱锥中,平面,平面,为垂足,在三棱锥内,类比射影定理,探究这三者之间满足的关系是.PADCBE15.用若干个体积为1的正方体搭成一个几何体,其正(主)视图、侧(左)视图都是如图所示的图形,则这个几何体的最大体积是___16..如图,将菱形ABCD沿对角线BD折起,使得C点至,E点在线段上,若二面角A—BD-E与二面角的大小分别为30°和45°,则=._______三.解答题:(74分)17.(本小题满分12分)如图,四棱锥P-ABCD中,PA面ABCD.底面ABCD为直角梯形,121,90ADBCABPABADABC。E为PD的中点。(1)求证://CE平面PAB;(2)求异面直线AB与PC所成的角的正切值。18.(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC.AB=AC=l,∠BAC=120,异面直线B1C与A1C1所成的角为60°。(I)求三棱柱ABC-A1B1C1的体积:(II)求二面角B1-AC-B的余弦值.19.(本题满分12分)如图,已知矩形的边与正方形所在平面垂直,,,是线段的中点。(1)求证:平面;(2)求二面角的大小。20.(本小题12分)如图,在四棱锥中,平面,四边形是菱形,,,E是PB上任意一点.(I)求证:AC⊥DE;(II)已知二面角的余弦值为,若为的中点,求与平面所成角的正弦值.PEDOCBAO21.(本小题满分12分)如图所示,四棱锥P-ABCD的底面是边长为1的正方形,PACD,PA=1,PD=,E为PD上一点,PE=2ED.(Ⅰ)求证:PA平面ABCD;(Ⅱ)求二面角D-AC-E的余弦值;(Ⅲ)在侧棱PC上是否存在一点F,使得BF//平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.22.(本小题共14分)如图边长为4的正方形所在平面与正所在平面互相垂直,分别为的中点.(1)求证:平面;(2)求:二面角的余弦值;(3)试问:在线段上是否存在一点使得平面平面若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.望子成龙学校高二上数学半期摸拟题答案一,选择题:(60分)ADBADCBBCADC二.填空题:(16分)13.答:32.14.答:15.答:11. 体积最大时,底层有9个小正方体,左上面有2个小正方体。16.答:三.解答题:(74分)17.解:1)取AD的中点F...