山西省孝义市高二数学3月阶段性考试试卷 理(PDF)答案 山西省孝义市高二数学3月阶段性考试试卷 理(PDF) 山西省孝义市高二数学3月阶段性考试试卷 理(PDF)VIP免费

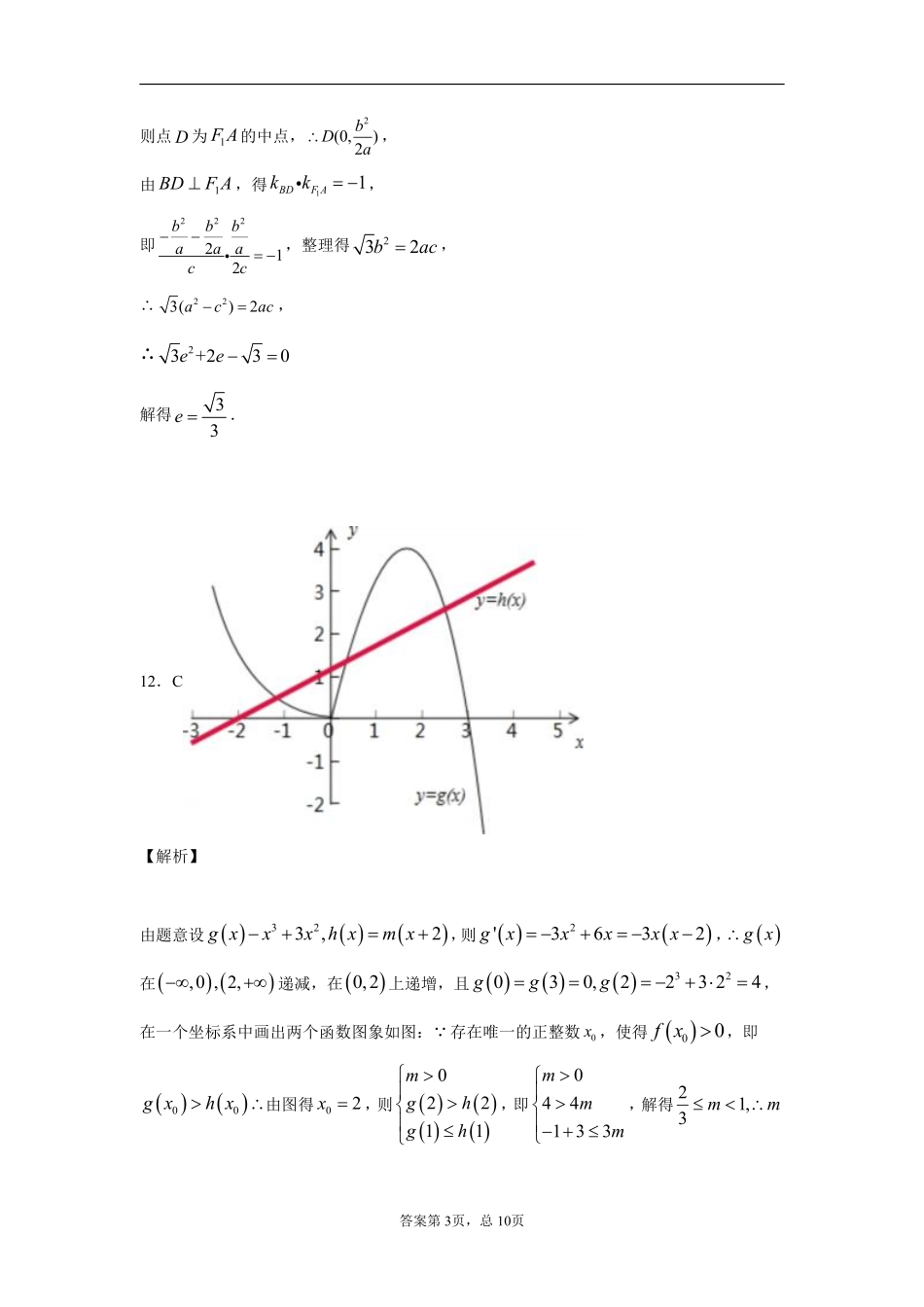
答案第1页，总10页参考答案1．Bv＝s′(t)＝gt，∴当t＝3时，v＝3g＝29.4.选B2．C由00111111limlim'1333xxffxfxffxx，0111lim'133xffxfx，故选C.3．A f（x）=x2+2f′（2）x+m，∴f′（x）=2x+2f′（2），∴f′（2）=2×2+2f′（2），∴f′（2）=﹣4．∴f（x）=x2﹣8x+m，其对称轴方程为：x=4，∴f（0）=m，f（5）=25﹣40+m=﹣15+m，∴f（0）＞f（5）．4．C在A中，-sin-cosx=-cos-cos-=0xdx，在B中，根据定积分的几何意义，122011xdx=1=44，在C中，11002dx=2202x，根据定积分的运算法则与几何意义，易知102211xdxxdx+120xdx=1202xdx，5．A 函数f(x)＝x3－ax2＋1在(0，2)内单调递减，∴f′(x)＝3x2－2ax≤0在(0，2)内恒成立，即a≥32x在(0，2)内恒成立． 32x<3，∴a≥3.6．D因为32()26fxxxm，所以2'()6126(2)fxxxxx，可以得到函数在[2,0]上答案第2页，总10页是增函数，在[0,2]上是减函数，所以当0x时，()fxm为最大值，所以3m，即32()263fxxx，所以(2)2(8)64337,(2)5ff，所以最小值是37，故选D.7．C20fxdx＝122012xdxxdx＝31220111|2|32xxx115422326，故选C.8．B由题可知长方形面积为3，而长方形空白部分面积为：11001|2xxedxexe，故所求概率为25133ee，9．Dsincos2fxxxxx，'cossinfxxxx．易知'fx是偶函数，排除A，'01f，排除B，'f()1又排除C．识图常用的方法(1)定性分析法：通过对问题进行定性的分析，从而得出图象的上升(或下降)的趋势，利用这一特征分析解决问题；(2)定量计算法：通过定量的计算来分析解决问题；(3)函数模型法：由所提供的图象特征，联想相关函数模型，利用这一函数模型来分析解决.10．A设圆柱的底面半径为r，高为h．∴4r+2h=l，∴42lrh．∴圆柱体积233224224()()8836rrlrlVrhrrlr（）．当且仅当6lr时取等号．11．D由题意可得，2(,)bAca，2(,)bBca，答案第3页，总10页则点D为1FA的中点，2(0,)2bDa，由1BDFA，得11BDFAkk，即222212bbbaaacc，整理得232bac，223()2acac，∴23+230ee解得33e．12．C【解析】由题意设323,2gxxxhxmx，则2'3632gxxxxx，gx在,0,2,递减，在0,2上递增，且32030,22324ggg，在一个坐标系中画出两个函数图象如图：存在唯一的正整数0x，使得00fx，即00gxhx由图得02x，则02211mghgh，即044133mmm，解得21,3mm答案第4页，总10页的取值范围是2,13，故选C.13．46抛物线E：x2=4y的焦点为（0，1），准线为y=﹣1．（0，1）代入圆C：x2+y2+8x+ay﹣5=0，可得1+a﹣5=0，∴a=4∴圆C：x2+y2+8x+4y﹣5=0，即（x+4）2+（y+2）2=25，∴圆心到直线的距离为d=1，∴抛物线E的准线与圆C相交所得的弦长为225146．故答案为4614．125S10=30(1+2x)dx=(x+x2)|3030=3+9=12.因为{an}是等差数列，所以，S10=5610aa2=5(a5+a6)=12，所以a5+a6=125.故答案为：12515．(,2)(02)， fxfx，∴函数fx为偶函数．设()()fxhxx，则2()()()xfxfxhxx， 当0x时，0xfxfx，∴当0x时()0hx，函数()hx单调递增．答案第5页，总10页又函数()hx为奇函数，∴当0x时，函数()hx单调递增．由20f得(2)(2)0hh．画出函数()hx的大致图象如图所示．由图象可得不等式()0hx的解集为(,2)(02)，．又不等式0xfx的解集与不等式()0hx的解集相同，∴不等式0xfx的解集是(,2)(02)，．故答案为(,2)(02)，．16．③④根据题意...