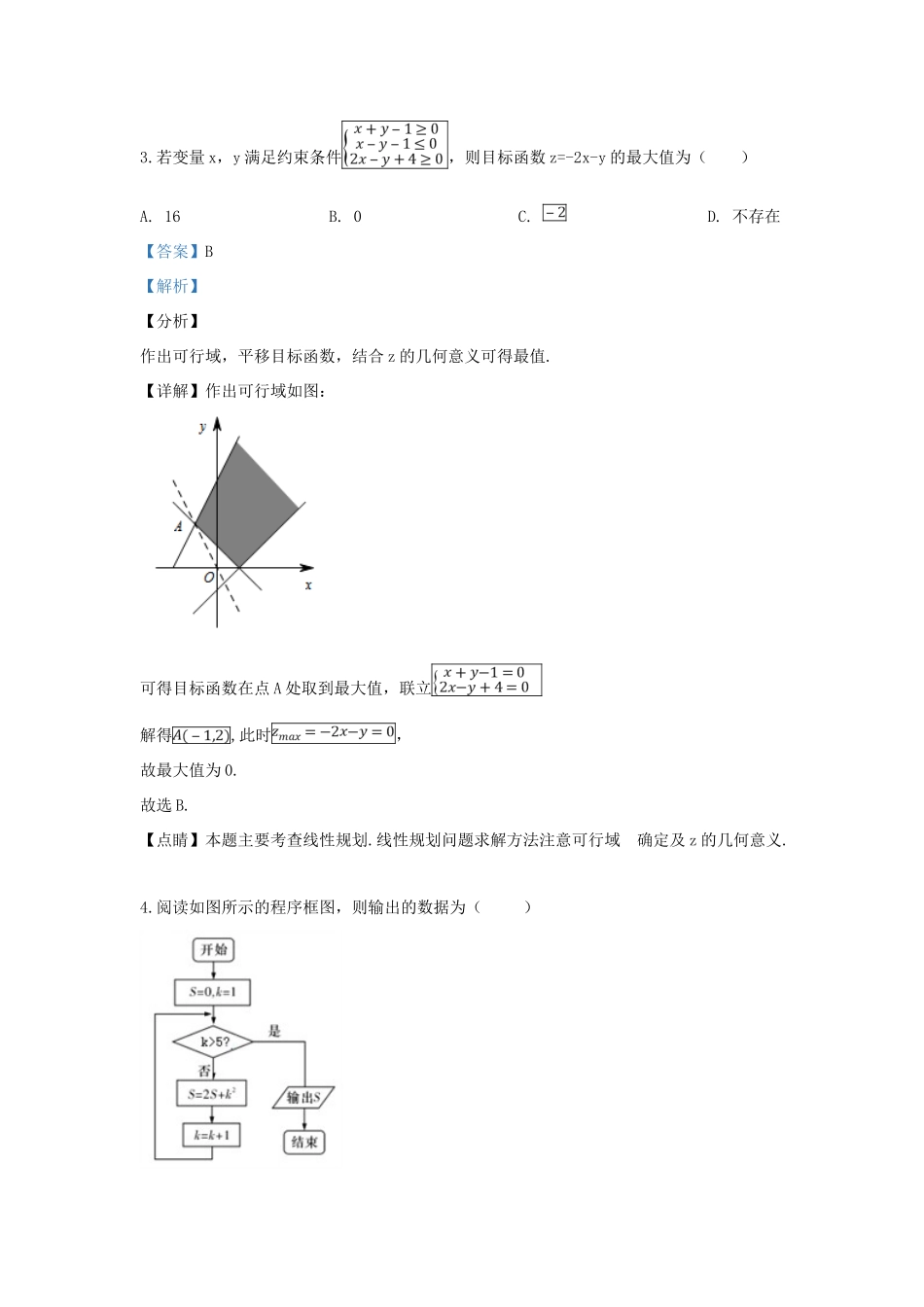
天津市2019届高三4月份联考数学试题一、选择题(本大题共8小题,共40.0分)1.设全集,集合,,则()A.B.C.D.【答案】D【解析】【分析】首先求出集合,然后再求出集合的补集,然后再根据集合的交集运算即可求出结果.【详解】由于,所以,所以,故选D.【点睛】本题主要考查集合的补集、交集运算,熟练掌握补集、交集的运算公式是解决问题的关键.2.设,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】【分析】首先解出不等式和,然后再根据充分必要条件的定义即可求出结果.【详解】由,得;由,得或;所以“”是“”的充分不必要条件,故选A.【点睛】本题主要考查充分条件和必要条件的判断,比较基础.3.若变量x,y满足约束条件,则目标函数z=-2x-y的最大值为()A.16B.0C.D.不存在【答案】B【解析】【分析】作出可行域,平移目标函数,结合z的几何意义可得最值.【详解】作出可行域如图:可得目标函数在点A处取到最大值,联立解得,此时,故最大值为0.故选B.【点睛】本题主要考查线性规划.线性规划问题求解方法注意可行域的确定及z的几何意义.4.阅读如图所示的程序框图,则输出的数据为()A.21B.58C.141D.318【答案】C【解析】经过第一次循环得到的结果为,;经过第二次循环得到的结果为,;经过第三次循环得到的结果为,;经过第四次循环得到的结果为,;经过第五次循环得到的结果为,,此时输出结果.故选C.5.抛物线的准线与双曲线的两条渐近线所围成的三角形面积为,则的值为()A.B.C.D.【答案】A【解析】【分析】求得抛物线的准线方程和双曲线的渐近线方程,解得两交点,由三角形的面积公式,计算即可得到所求值.【详解】抛物线的准线为,双曲线的两条渐近线为,可得两交点为,即有三角形的面积为,解得,故选A.【点睛】本题考查三角形的面积的求法,注意运用抛物线的准线方程和双曲线的渐近线方程,考查运算能力,属于基础题.6.的图像经过怎样的平移后所得的图像关于点中心对称()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【答案】C【解析】【分析】设出将函数y=sin(2x+)的图象平移ρ个单位得到关系式,然后将x=﹣代入使其等于0,再由正弦函数的性质可得到ρ的所有值,再对选项进行验证即可.【详解】假设将函数y=sin(2x+)的图象平移ρ个单位得到y=sin(2x+2ρ+)关于点(﹣,0)中心对称∴将x=﹣代入得到sin(﹣+2ρ+)=sin(+2ρ)=0∴+2ρ=kπ,∴ρ=﹣+,当k=0时,ρ=﹣,向右平移,故选:B.【点睛】本题考查的是三角函数的平移问题,首先保证三角函数同名,不是同名通过诱导公式化为同名,在平移中符合左加右减的原则,在写解析式时保证要将x的系数提出来,针对x本身进行加减和伸缩.7.已知定义在上的函数满足,且对任意(0,3)都有,若,,,则下面结论正确的是()A.B.C.D.【答案】C【解析】【分析】由条件,可知函数关于对称,由对任意(0,3)都有,可知函数在(0,3)时单调递减,然后根据单调性和对称性即可得到的大小.【详解】因为,得函数关于对称,又对任意(0,3)都有,所以函数在(0,3)时单调递减,因为,所以,又,所以,所以,故选C.【点睛】本题主要考查函数值的大小比较,利用条件求出函数的单调性和对称性,利用单调性和对称性之间的关系是解决本题的关键.8.边长为的菱形中,与交于点,是线段的中点,的延长线与相交于点.若,则()A.B.C.D.【答案】B【解析】【分析】根据两个三角形相似对应边成比例,得到,运用向量的加减运算和向量中点的表示,结合向量数量积的定义和性质,向量的平方即为模的平方,将向量用表示,利用数量积公式计算即可得到结果.【详解】由题意可知,做出菱形ABCD的草图,如下图:由题意易知,,可得,所以,又,所以,故选B.【点睛】本题考查平面向量的基本定理,向量数量积的定义及性质,考查了学生的归纳分析能力,和运算能力,属于中档题.二、填空题(本大题共6小题,共30.0分)9.设复数,则=__________.【答案】【解析】【分析】利用复数代数形式的乘除运算化简得到,再由共轭复数的概念得到,进而求出结果.【详解】.【点睛】本题考查...