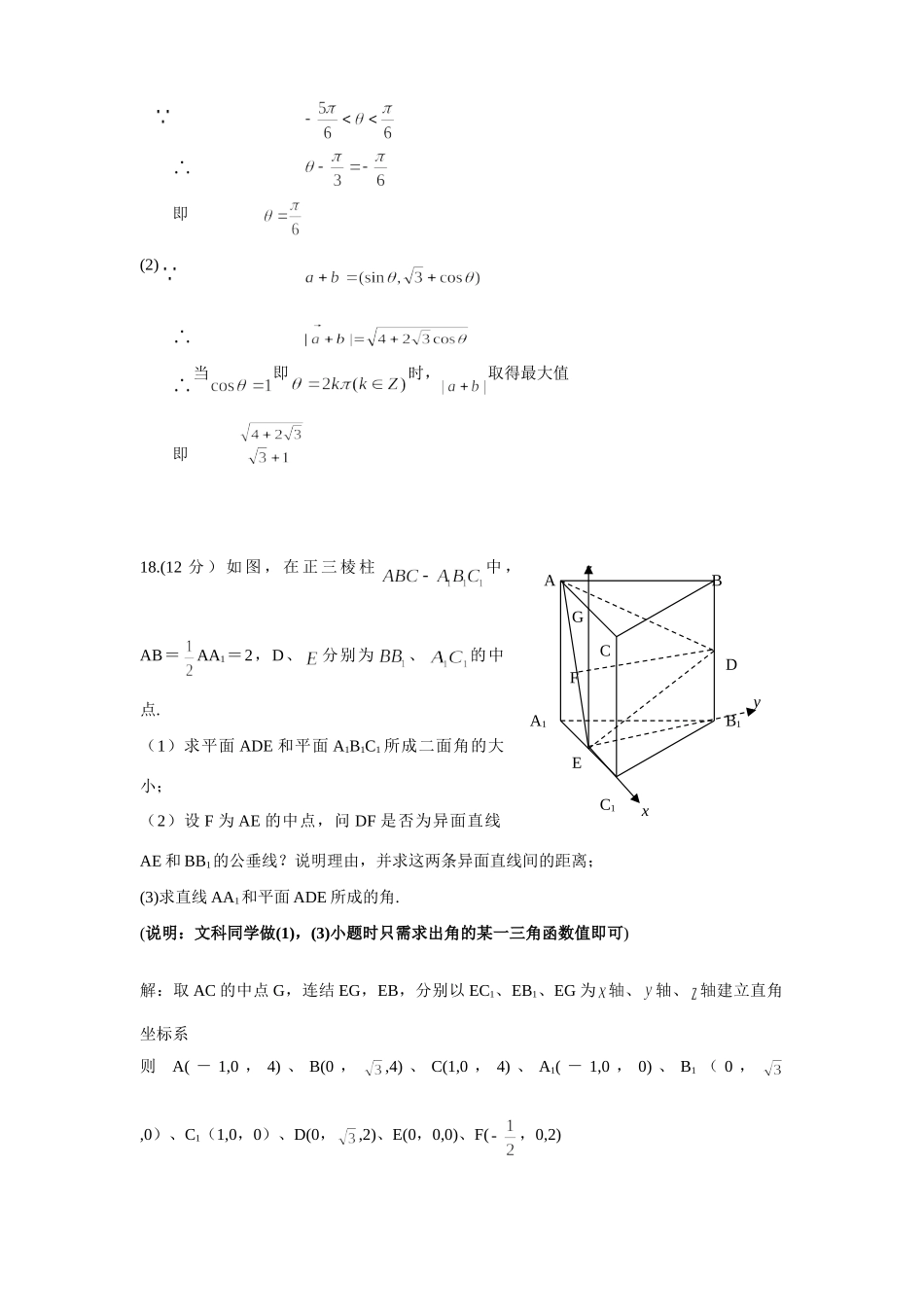
四川省成都市新都一中高2007级高三数学10月月考试卷命题人:陈靖一、选择题(60分)1.若,且,则的取值范围是A.B.C.D.2.若与都是非零向量,则“”是“//()”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.若至少存在一个实数,使得不等式成立,则满足A.B.C.或D.或4.已知双曲线的一条渐近线方程为,则双曲线的离心率为A.B.C.D.5.已知,且是递增的数列,则实数λ取值范围是A.λ0B.λC.λD.λ>-36.若函数满足1,成等差数列,则的反函数是A.y=(x>0)B.y=(x<0)C.y=(x>0)D..y=(x<0)7.在等比数列中,,前项和为,若数列也是等比数列,则等于(A)(B)(C)(D)8.若数列中,,当时则数列的通项公式等于A.B.C.D.9.已知二次函数(其中是的三条边长)则函数的定义域M和值域P的关系是A.M=PB.PMC.MPD.由的值而定.10.(理科)设函数,集合M=,P=(其中是的导函数),若MP,则实数a的取值范围是A.(-∞,1)B.(0,1)C.(1,+∞)D.[1,+∞10.(文科))已知曲线,则过点(1,2)的切线的斜率是(A)2(B)4(C)6(D)811.函数的最小值是A.B.C.D.12.在正方体上取4个顶点作为四面体的顶点,则所得的四面体是正四面体的概率为A.B.C.D.一、选择题CACADACCBCAB二、填空题(16分)13在的展开式中常数项是(用数字作答)14.已知∈(,2),sin=,则tan()等于15.已知是定义在R上的奇函数,且,则016.已知是上的减函数,那么的取值范围是三、解答题(74分)17.(12分)已知向量.(1)若且求;(2)求的最大值。解:(1)由得即即(2)当即时,取得最大值即18.(12分)如图,在正三棱柱中,AB=AA1=2,D、分别为、的中点.(1)求平面ADE和平面A1B1C1所成二面角的大小;(2)设F为AE的中点,问DF是否为异面直线AE和BB1的公垂线?说明理由,并求这两条异面直线间的距离;(3)求直线AA1和平面ADE所成的角.(说明:文科同学做(1),(3)小题时只需求出角的某一三角函数值即可)解:取AC的中点G,连结EG,EB,分别以EC1、EB1、EG为轴、轴、轴建立直角坐标系则A(-1,0,4)、B(0,,4)、C(1,0,4)、A1(-1,0,0)、B1(0,,0)、C1(1,0,0)、D(0,,2)、E(0,0,0)、F(,0,2)ABCA1B1C1DExyzGF(1)设平面ADE的法向量为,,由可得取,得又平面A1B1C1的法向量为,所以平面ADE和平面A1B1C1所成二面角为或(2)与不垂直,即DF不是EA与B1B的公垂线,又所以B1E是EA与B1B的公垂线,EA与B1B的距离为(3)由(1)知所以A1A与平面ADE所成角为即19.(12分)已知和中,是关于的方程的二根,设.(1)求的最大值;(2).解:由已知得解得,(1),当时,;当时,,即的最大值为1;(2)令,则,=所以20.(12分)袋中装着标有数字1,2,3,4的小球各2个,从袋中任取2个小球,若取出两球数字相同,则计4分,若取出两球数字不同则用较大数字减去较小数字作为得分,每个小球被取出的可能性都相等.求:①取出的2个小球上的数字互不相同的概率;②(理)用表示取出的2个小球的得分,求随机变量的概率分布和数学期望.②(文)求取出两球的得分不超过3分的概率.解:①用A表示事件“取出的2个小球上的数字互不相同”则P(A)=(或P(A)=)答:取出的2个小球上的数字互不相同的概率是②(理)由题意有,且,,,.答:随机变量的概率分布为数学期望为②(文)用Ak(k=1,2,3)表示事件“取出两球的得分为k”则,,,所以,取出两球的得分不超过3分的概率为++=答:取出两球的得分不超过3分的概率.21.(理科)(13分)已知函数(为常数),函数在上是增函数,求的取值范围.21.(文科)(13分)设函数,已知是奇函数。(Ⅰ)求、的值;(Ⅱ)求的单调区间与极值.解:(理),,由题意有当时即恒成立.令=下面求函数=()的最大值1234P=,由=0()得,当时>0,即在上是增函数;当时<0,即在上是减函数.所以当时,=()取得最大值.(文)是奇函数,,由=0得,当变化时的关系如下表所示:+0-0+极大极小因此,函数递增区间有和,递减区间有,当时,极大极为;当时取极小值.22.(13分)双曲线的半焦距等于实轴的长,且为它的右准线.(Ⅰ)求此双曲线的方程;(Ⅱ)(理科)若数列,且满足点在双曲线上,求证:.(Ⅱ)(文科)若数列,且满足点在双曲线上,求数列的通项公式.解:(Ⅰ)由已知得解得双曲线方程为(Ⅱ)由题意有,即,亦即令,则即又(文科至此解答完毕)(理科)即成立.