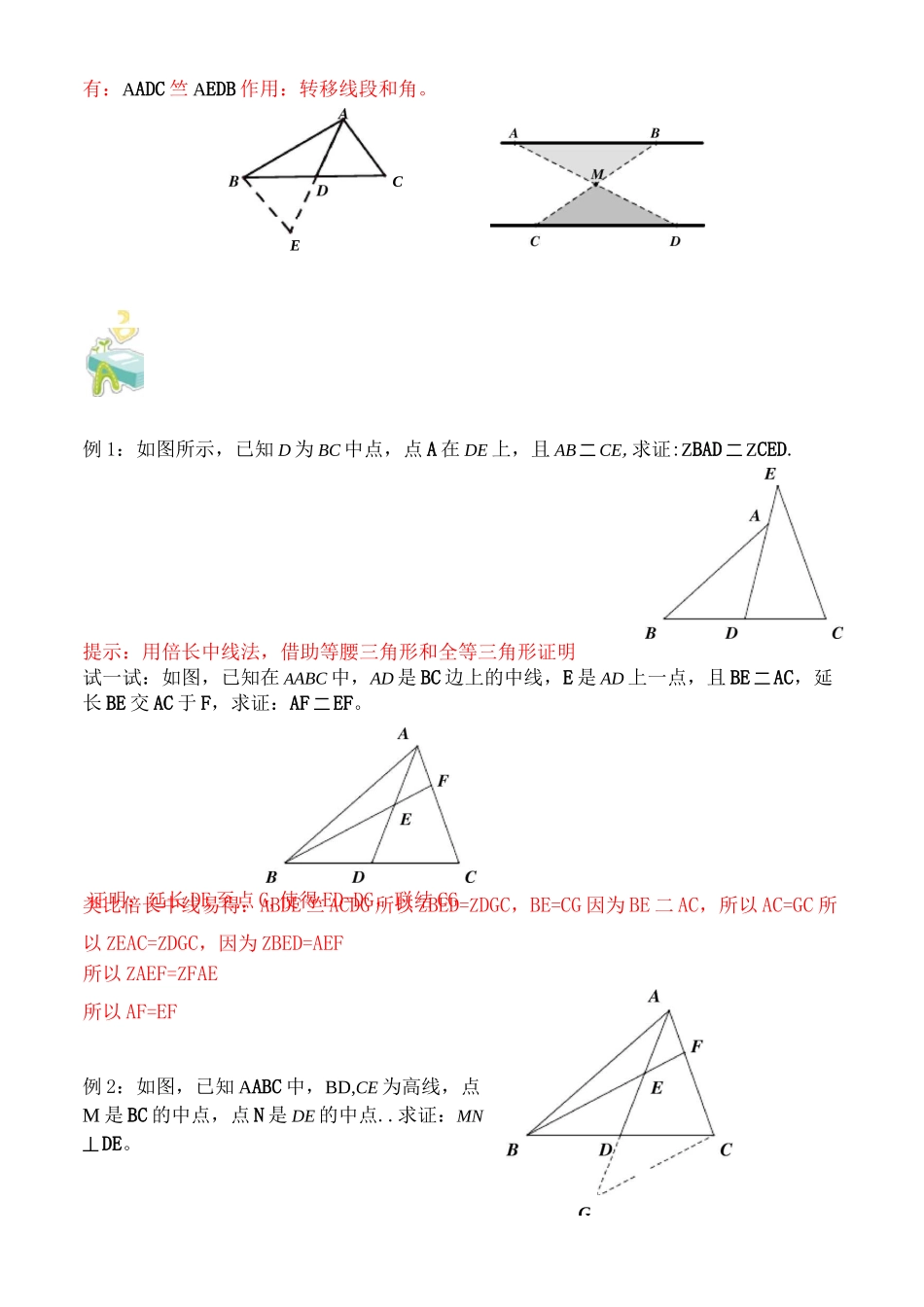
初中数学突破中考压轴题几何模型之中点模型教案集团标准化工作小组[Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]则有:CD=AD=BD=2AB2.三线合一:在AABC中:(1)AC二BC;(2)CD平分ZACB“知二得二”:比如由(2)(3)可得出(1)(4)择两个作为条件,就可以推出余下两条。(3)AD=BD,(4)CD丄AB.也就是说,以上四条语句,任中点模型教学内容学习过中位线之后,你能否总结一下,目前我们学习了哪些定理或性质与中点有关直角三角形中点你想到了什么,等腰三角形中点你想到了什么,一般三角形中点你又想到了什么1.直角三角形斜边中线定理:如图,在RtAABC中,ZACB=90。,D为AB中点,3.中位线定理:如图,在AABC中,若AD二BD,AE二CE,则DE//BC且DE=2BC24.中线倍长(倍长中线):如图(左图),在AABC中,D为BC中点,延长AD到E使DE=AD,联结BE,则A授课日期证明:延长DE至点G,使得ED=DG,联结CG有:AADC竺AEDB作用:转移线段和角。例1:如图所示,已知D为BC中点,点A在DE上,且AB二CE,求证:ZBAD二ZCED.提示:用倍长中线法,借助等腰三角形和全等三角形证明试一试:如图,已知在AABC中,AD是BC边上的中线,E是AD上一点,且BE二AC,延长BE交AC于F,求证:AF二EF。类比倍长中线易得:ABDE竺ACDG所以ZBED=ZDGC,BE=CG因为BE二AC,所以AC=GC所以ZEAC=ZDGC,因为ZBED=AEF所以ZAEF=ZFAE所以AF=EF例2:如图,已知AABC中,BD,CE为高线,点M是BC的中点,点N是DE的中点..求证:MN丄DE。CEG证明:联结EM、DM在RtABEC中EM=1BC,在RtABDC中DM=-BC22所以EM=DM,又因为EN=ND,所以MN丄DE例3:如图,在AABC中,AD为ZA的平分线,M为BC的中点,AD//ME,求证:BE=CF=1%+AC)。证明:延长FM至点G,使得FM=MG,联结BG类比倍长中线易得:△^MG^^CMF所以ZG=ZCFM,BG=CF因为AD〃EM,所以ZBAD=ZE,ZDAF=ZEFA因为ZBAD=ZDAC,ZAFE=ZCFM所以ZE=ZAFE=ZCFM=ZG所以BE二BG二CF,AE=AF因为AB+AC二AB+AF+FC二AB+AE+BE二BE+BE=2BE所以BE=CF=1(AB+AC)2试一试:如图所示,在ABC中,AC>AB,M为BC的中点,AD是ABAC的平分线,若CF丄AD且交AD的延长线于F,求证:MF=1(AC-AB)。提示:延长AB,CF交于点E,证明出BE=AC-AB,再根据中位线的性质就可得证提示:延长AE、BC交于点F,易证△ADE^^FCE,得AD=CF,AE=EFO因为AB二AD+BC,所以AB=BF,所以AE丄BE2.如图,已知:AABC中,ZA二90。,D是BC的中点,DE丄DF。求证:BE2+CF2=EF2证明:延长ED至点G,使得ED=DG,联结CG、FG'BD=DC因为