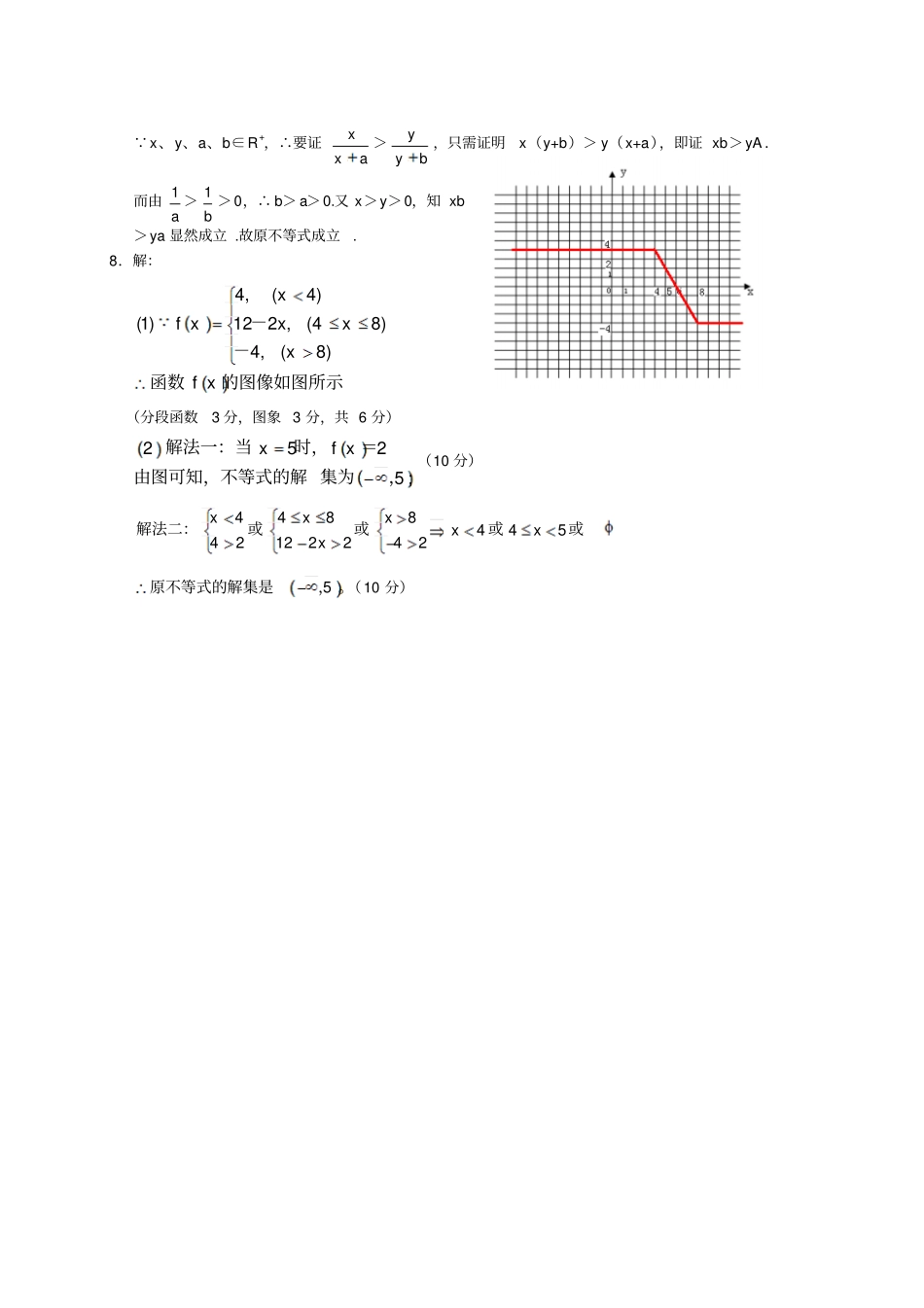
高中数学学习材料(灿若寒星精心整理制作)高中数学选修4-5模块考试一、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知c<d,a>b>0,下列不等式中必成立的一个是()A.a+c>b+dB.a–c>b–dC.ad<bcD.dbca2.函数28(0)2xyxx的最大值是()A.6B.8C.10D.183.已知函数f(x)=-2x+1,对于任意正数,使得|f(x1)-f(x2)|<成立的一个充分但不必要条件是A.|x1-x2|44.用数学归纳法证明“nnnnn212111211214131211”时,由kn的假设证明1kn时,如果从等式左边证明右边,则必须证得右边为()A.1212111kkkB.2211212111kkkkC.1212121kkkD.22112121kkk二、填空题(本大题共2小题,每小题5分,共10分)5.若14a,24b,则2a-b的取值范围是.6.函数220()5(0)fxxxx的最小值为_____________.三、解答题(本大题共2小题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.)7.(本小题10分)已知a、b、x、y均为正实数,且a1>b1,x>y.求证:axx>byy.8.(本小题10分)已知函数()|8||4|fxxx.(Ⅰ)作出函数y=f(x)的图像:(Ⅱ)解不等式|8||4|2xx.高中数学选修4-5模块考试参考答案一、选择题BACD二、填空题5.)10,2(6.15三、解答题7.证法一:(作差比较法)∵axx-byy=))((byaxaybx,又a1>b1且a、b∈R+,∴b>a>0.又x>y>0,∴bx>ay.∴))((byaxaybx>0,即axx>byy.证法二:(分析法)xy011∵x、y、a、b∈R+,∴要证axx>byy,只需证明x(y+b)>y(x+a),即证xb>yA.而由a1>b1>0,∴b>a>0.又x>y>0,知xb>ya显然成立.故原不等式成立.8.解:的图像如图所示函数--xf8)(x4,8)x(42x,124)(x,4xf)1((分段函数3分,图象3分,共6分);52xf5x2,集为由图可知,不等式的解=时,解法一:当(10分)448844542122242解法二:或或或或xxxxxx5原不等式的解集是,。(10分)