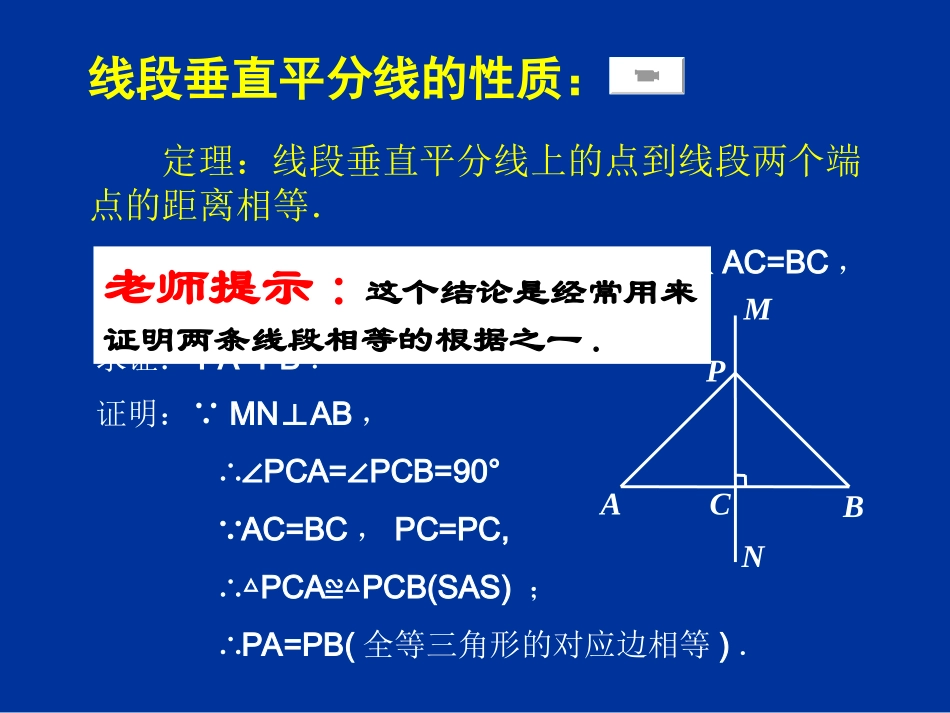
修改者:2015年3月21日用心想一想,马到功成如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?AB线段垂直平分线的性质:定理:线段垂直平分线上的点到线段两个端点的距离相等.已知:如图,直线MNAB⊥,垂足是C,且AC=BC,P是MN上的点.求证:PA=PB.NAPBCM证明: MNAB⊥,∴∠PCA=PCB=90°∠ AC=BC,PC=PC,∴△PCAPCB(SAS)≌△;∴PA=PB(全等三角形的对应边相等).老师提示:这个结论是经常用来证明两条线段相等的根据之一.用心想一想,马到功成你能写出上面这个定理的逆命题吗?它是真命题吗?如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.即到线段两个端点的距离相等的点在这条线段的垂直平分线上.当我们写出逆命题时,就想到判断它的真假.如果真,则需证明它;如果假,则需用反例说明.已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.证明:过点P作已知线段AB的垂线PC,PA=PB,PC=PC,∴RtPACRtPBC(HL)△≌△.∴AC=BC,即P点在AB的垂直平分线上.CBPA证法二:取AB的中点C,过P,C作直线. AP=BP,PC=PC.AC=CB,∴△APCBPC(SSS)≌△.∴∠PCA=PCB(∠全等三角形的对应角相等).又 ∠PCA+PCB=180°∠,∴∠PCA=PCB=90°∠∠,即PCAB⊥∴P点在AB的垂直平分线上.CBPA已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.CBPA已知:线段AB,点P是平面内一点且PA=PB.求证:P点在AB的垂直平分线上.证法三:过P点作∠APB的角平分线交AB于点C. AP=BP,∠APC=BPC∠,PC=PC,∴△APCBPC(SAS)≌△.∴AC=BC,∠PCA=PCB∠又 ∠PCA+PCB=180°PCA=PCB=90°∠∴∠∠∴P点在线段AB的垂直平分线上.线段垂直平分线的判定:定理:到线段两个端点的距离相等的点在这条线段的垂直平分线上.ABCAB=AC,OABCOB=OC.AOBC例1如图在△中,是△内一点,且求证:直线垂直平分线段证明: AB=ACABC点在线段的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)OBC同理,点在线段的垂直平分线上AOBC直线是线段的垂直平分线(两点确定一条直线)ABCO你还有其他证明方法吗?想一想,做一做用尺规作线段的垂直平分线.已知:线段AB.求作:线段AB的垂直平分线.作法:1.分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点C和D.2.作直线CD.直线CD就是线段AB的垂直平分线.DCBA老师提示:因为直线CD与线段AB的交点就是AB的中点,所以我们也用这种方法作线段的中点.1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED=cm;如果∠ECD=60°,那么∠EDC=.CADBE760°2.已知直线l和l上一点P,利用尺规作l的垂线,使它经过点P.已知:直线l和l上一点P.求作:PC⊥l.作法:1、以点P为圆心,以任意长为半径作弧,与直线l相交于点A和B.2.作线段AB的垂直平分线PC.直线PC就是所求的垂线.lPABC线段的垂直平分线的性质定理的逆定理逆定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.ACBPMN如图, PA=PB(已知),∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.从这个结果出发,你还能联想到什么?回顾思考利用尺规作三角形三条边的垂直平分线,当作完此题时你发现了什么?用心想一想,马到功成发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.剪一个三角形纸片,通过折叠找出每条边的垂直平分线,观察这三条垂直平分线,你是否发现同样的结论?与同伴交流.QPNMFECBAO思考分析命题:三角形三条边的垂直平分线相交于一点.如图,在△ABC中,设AB,BC的垂直平分线相交于点P,连接AP,BP,CP. 点P在线段AB的垂直平分线上,∴PA=PB(或AB的中点,).同理,PB=PC.∴PA=PC.∴点P在线段AC的垂直平分线上,∴AB,BC,AC的垂直平分线相交于一点.咋证三条直线交于一点基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第...