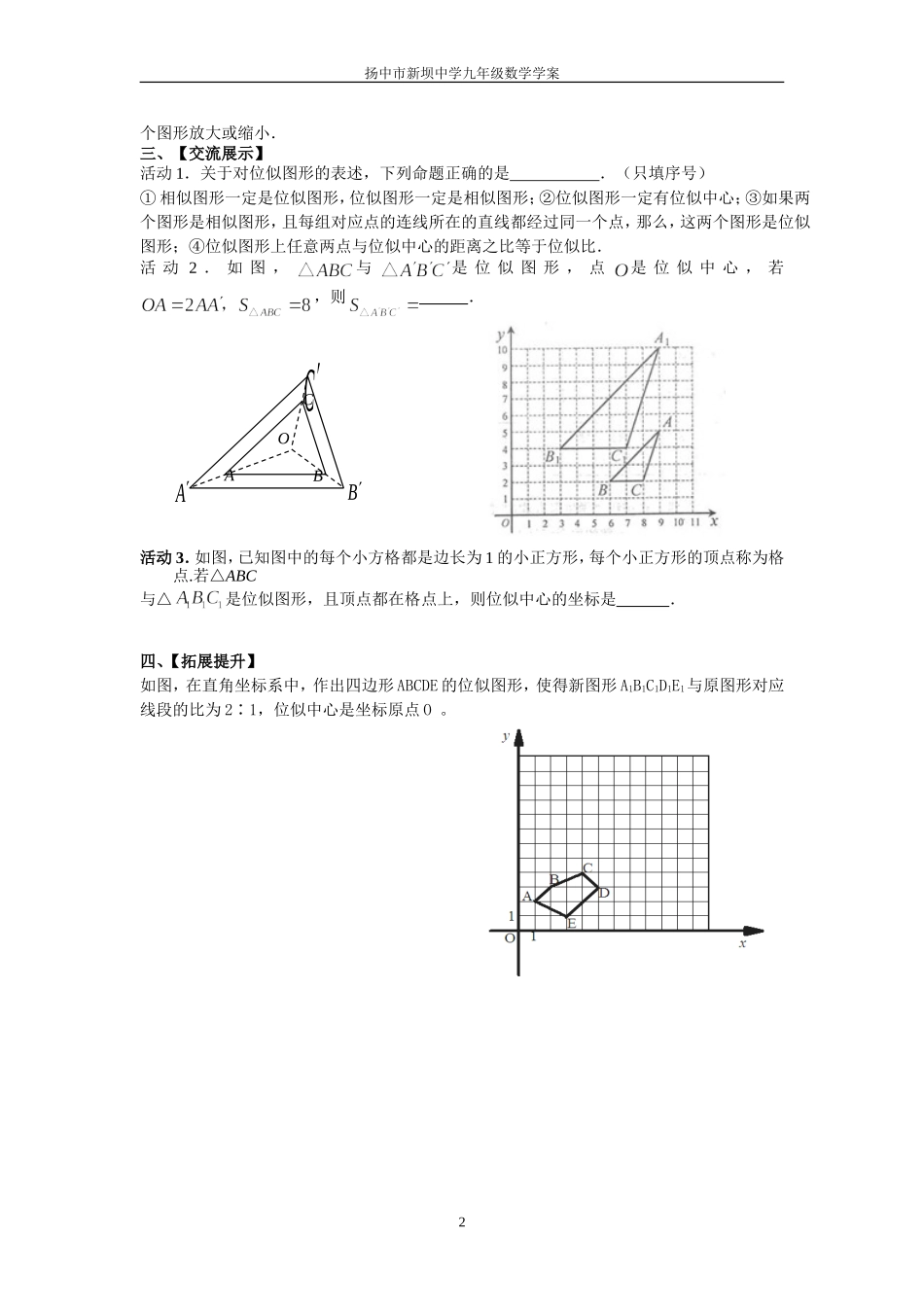
扬中市新坝中学九年级数学学案第10课时图形的位似【学习目标】1、了解位似图形的意义,能根据位似图形的特征,将一个图形进行放大和缩小。2、理解位似图形的性质、选择适当的方式进行图形的放大和缩小。3、从具体操作活动中,培养学生动手操作能力,空间想象能力。【学习重点】能根据位似图形的特征,将一个图形进行放大和缩小。【学习难点】理解位似图形的性质、选择适当的方式进行图形的放大和缩小。【学法指导】探索、合作、交流一、【前置学习】1.公安人员在侦破案件中,有时会从一枚指纹来确定罪犯的身份,最终破案。借助放大镜可以将它放大,保持形状不变。再如微型胶卷所拍摄的照片就是把实物缩小,保持形状不变。你还能举出生活中将一个图形放大或缩小的例子吗?如等。2.经过不同位似中心将同一图形进行放大和缩小,试问放大后的图形和缩小后的图形能否也是位似图形?谈谈你的看法。3.如图,已知ΔABC,过点O引OA并延长到A1,使OA1=2AO,请画出ΔA1B1C1,使ΔA1B1C1∽ΔABC。二、【合作释疑】1.已知点O和ΔABC,(1)画射线OA、OB、OC,分别在OA、OB、OC上取点A1、B1、C1,使画ΔA1B1C1.(2)分别在OA、OB、OC的反向延长线上取点A2'、B2、C2,使画ΔA2B2C2.(3)思考:ΔABC、ΔA1B1C1、ΔA2B2C2是否相似?为什么?2.归纳概括:(1)位似形:在上图中,两个多边形不仅,而且对应顶点的连线交于,对应边互相.像这样的两个图形叫做,这个点叫做位似.3.位似形的有关性质:(1)两个位似形一定是相似形;(2)各对对应顶点所在的直线都经过同一点;(3)各对对应顶点到位似中心的距离的比等于相似比.(4)利用位似形可以将一预习反馈1ABCO.ABCO.扬中市新坝中学九年级数学学案个图形放大或缩小.三、【交流展示】活动1.关于对位似图形的表述,下列命题正确的是.(只填序号)①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.活动2.如图,与是位似图形,点是位似中心,若,则.活动3.如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△是位似图形,且顶点都在格点上,则位似中心的坐标是.四、【拓展提升】如图,在直角坐标系中,作出四边形ABCDE的位似图形,使得新图形A1B1C1D1E1与原图形对应线段的比为2∶1,位似中心是坐标原点O。2COABBCA扬中市新坝中学九年级数学学案五、【巩固测评】1.如图,以O为位似中心,将四边形ABCD放大为原来的2倍.2.如图,以A为位似中心,将五角星缩小为原来的.3.如图,在12×12的正方形网格中,△TAB的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.4.如图,与是位似图形,且位似比是,若AB=2cm,则cm,并在图中画出位似中心O.检测反馈3.A.ABCDOTOBAxyABCABC扬中市新坝中学九年级数学学案六、【课后固学】A组题:1.如图(1)火焰的光线穿过小孔O,在竖直的屏幕上形成倒立的实像,像的长度BD=2cm,OA=60cm,OB=15cm,则火焰的长度为________.2.如图(2),五边形ABCDE与五边形A′B′C′D′E′是位似图形,且位似比为1:2.若五边形ABCDE的面积为17cm2,周长为20cm,那么五边形A′B′C′D′E′的面积为________,周长为________.3.已知,如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与________是位似图形,位似比为________;△OAB与________是位似图形,位似比为________.4.下列说法中正确的是()A.位似图形可以通过平移而相互得到B.位似图形的对应边平行且相等C.位似图形的位似中心不只有一个D.位似中心到对应点的距离之比都相等B组题:5.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图...