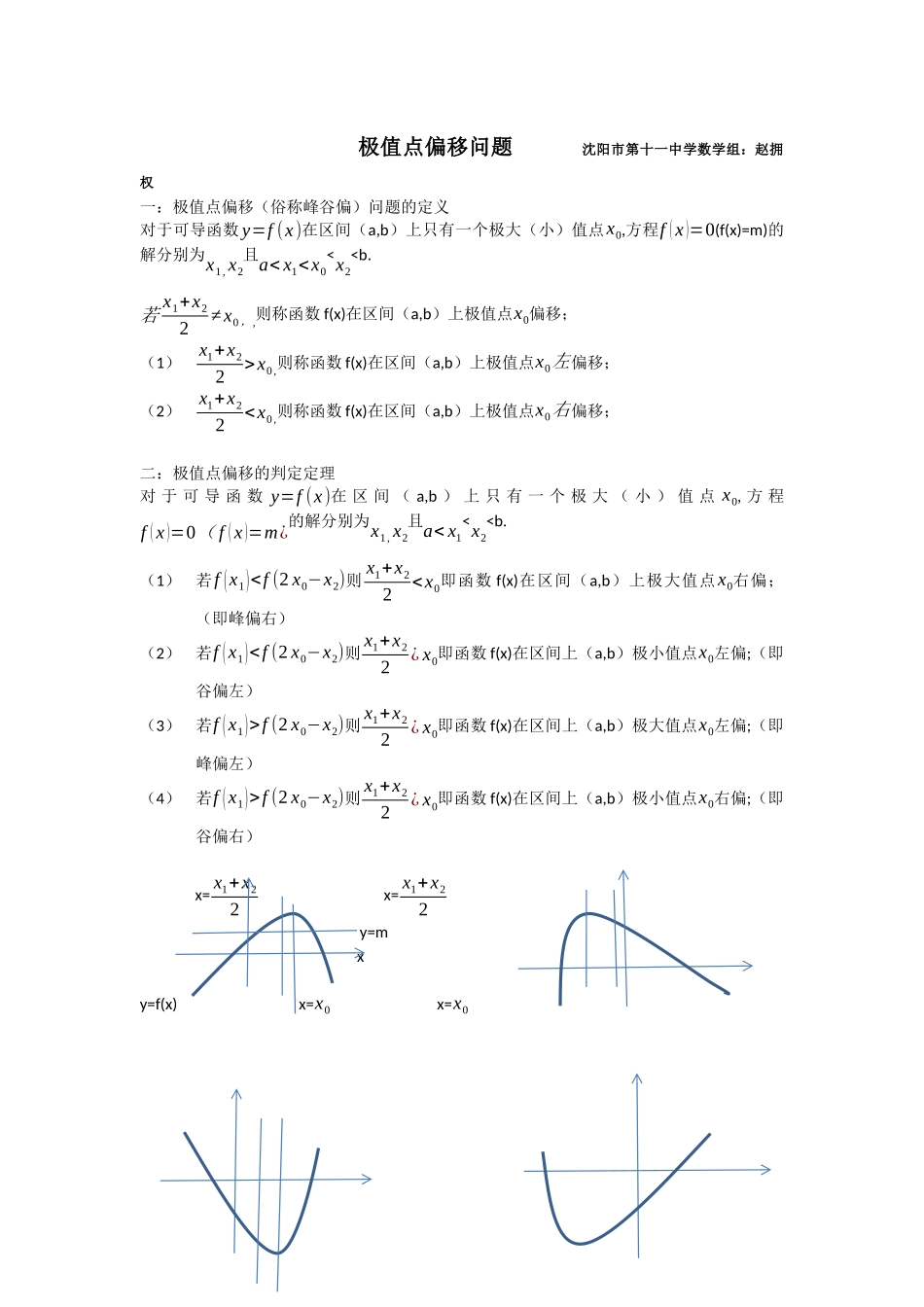
极值点偏移问题沈阳市第十一中学数学组:赵拥权一:极值点偏移(俗称峰谷偏)问题的定义对于可导函数y=f(x)在区间(a,b)上只有一个极大(小)值点x0,方程f(x)=0(f(x)=m)的解分别为x1,x2且ax0,则称函数f(x)在区间(a,b)上极值点x0左偏移;(2)x1+x22f(2x0−x2)则x1+x22¿x0即函数f(x)在区间上(a,b)极大值点x0左偏;(即峰偏左)(4)若f(x1)>f(2x0−x2)则x1+x22¿x0即函数f(x)在区间上(a,b)极小值点x0右偏;(即谷偏右)x=x1+x22x=x1+x22y=mxy=f(x)x=x0x=x0拓展:1)若f(a+x)=f(b−x),则f(x)的图象关于直线x=a+b2对称;特别地,若f(a+x)=f(a−x)(或f(x)=f(2a-x)),则f(x)的图象关于直线x=a对称2)若函数f(x)满足∀x∈(0,a)有下列之一成立:①f(x)在(0,a)递增,在(a,2a)递减,且f(a-x)<(>)f(a+x)(f(x)<(>)f(2a-x))②f(x)在(0,a)递减,在(a,2a)递增,且f(a-x)>(<)f(x+a)(f(x)>(<)f(2a-x))则函数f(x)在(0,2a)的图象关于直线x=a偏移(偏对称)(俗称峰谷偏函数)其中①极大值左偏(或右偏)也称峰偏左(或右)②极小值偏左(或偏右)也称谷偏左(或右);性质:1)f(x)的图象关于直线x=a对称若x1,x2∈(0,2a)x1≠x2则x1+x2=2a<=>f(x1)=f(x2),(f'(x1)+f'(x2)=0,f'(x1+x22)=0);2)已知函数是满足条件的极大值左偏(峰偏左)若x1,x2∈(0,2a)x1≠x2则f(x1)=f(x2)则x1+x2>2a,及f'(x1+x22)<0极值点偏移解题步骤:①求函数f(x)的极值点x0;②构造函数F(x)=f(x+x0)-f(x0−x¿(F(x)=f(x0−x)-f(x0+x¿,F(x)=f(x+2x0)-f(−x¿,F(x)=f(x)-f(2x0−x¿)确定F(x)单调性③结合F(0)=0(F(-x0)=0,F(x0¿=0¿判断F(x)符号从而确定f(x+x0),f(x0−x¿(f(x+2x0)与f(−x¿;f(x)与f(2x0−x¿)的大小关系;答题模式:已知函数y=f(x)满足f(x1)=f(x2),x0为函数y=f(x)的极值点,求证:x1+x2<2x0①求函数f(x)的极值点x0;②构造函数F(x)=f(x+x0)-f(x0−x¿确定F(x)单调性③判断F(x)符号从而确定f(x+x0),f(x0−x¿的大小关系;假设F(x)在(0,+∞)上单调递增则F(x)>F(0)=0,从而得到x>0时f(x+x0)>f(x0−x¿④1.(2016年全国I高考)已知函数有两个零点.设x1,x2是的两个零点,证明:+x2<2.2.(2010年高考天津卷理科21)(本小题满分14分)已知函数f(x)=xe-x(xR).(Ⅰ)求函数f(x)的单调区间和极值;(Ⅱ)已知函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称,证明当x>1时,f(x)>g(x)(Ⅲ)如果且证明证明:由题意可知g(x)=f(2-x),得g(x)=(2-x)令F(x)=f(x)-g(x),即于是当x>1时,2x-2>0,从而’(x)>0,从而函数F(x)在[1,+∞)是增函数。又F(1)=F(x)>F(1)=0,即f(x)>g(x).Ⅲ)证明:(1)若(2)若根据(1)(2)得由(Ⅱ)可知,>,则=,所以>,从而>.因为,所以,又由(Ⅰ)可知函数f(x)在区间(-∞,1)内事增函数,所以>,即>2.3.已知函数xaaxxxf)2(ln)(2.(I)讨论)(xf的单调性;(II)设0a,证明:当ax10时,)1()1(xafxaf;(III)若函数)(xfy的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f(x0)<0.解:(I)()(0,),fx的定义域为1(21)(1)()2(2).xaxfxaxaxx(i)若0,()0,()(0,)afxfx则所以在单调增加.(ii)若10,()0,afxxa则由得且当11(0,),()0,,()0.xfxxfxaa时当时所以1()(0,)fxa在单调增加,在1(,)a单调减少.(II)设函数11()()(),gxfxfxaa则3222()ln(1)ln(1)2,2()2.111gxaxaxaxaaaxgxaaxaxax当10,()0,(0)0,()0xgxggxa时而所以.故当10xa时,11()().fxfxaa………………8分(III)由(I)...