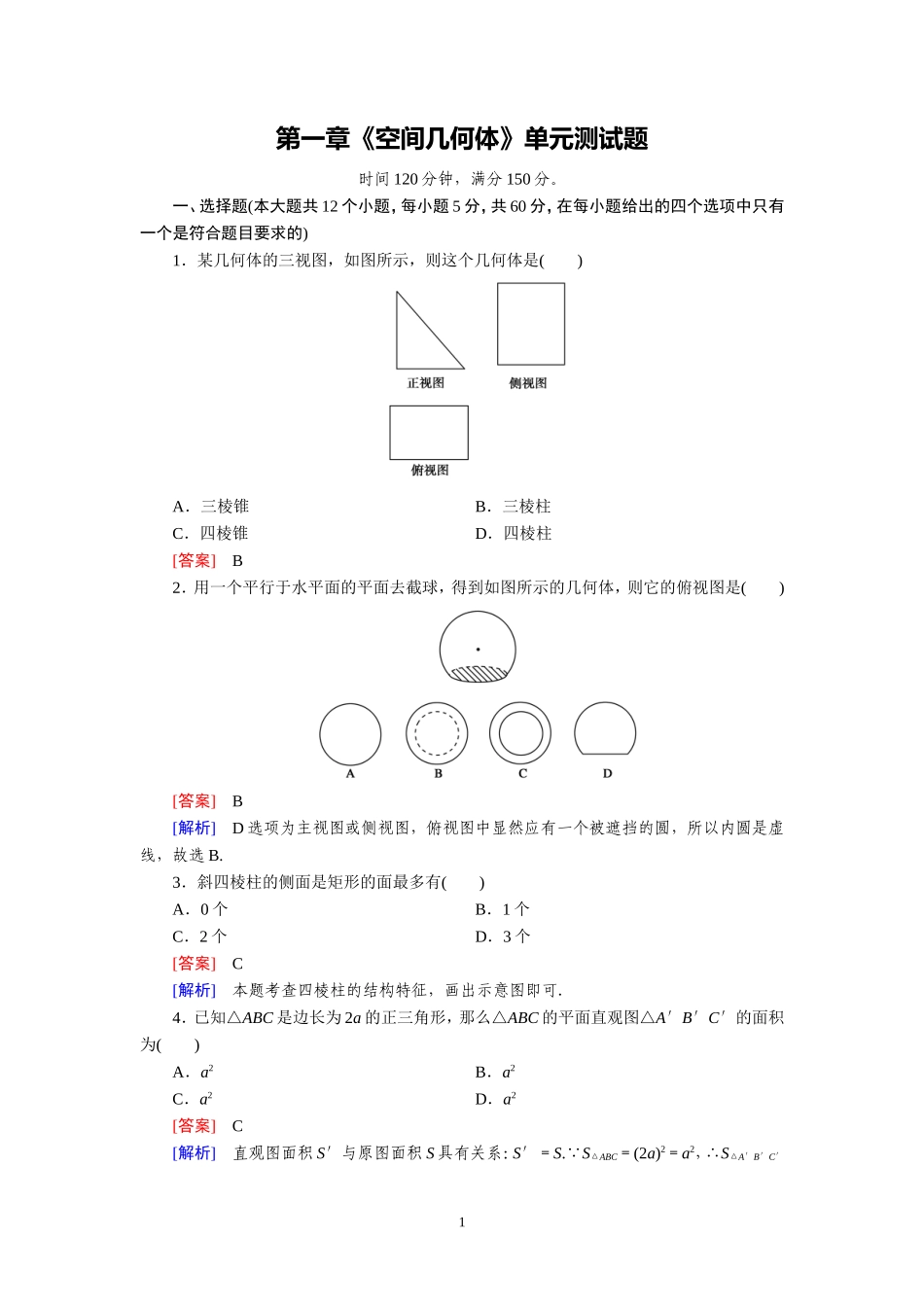
第一章《空间几何体》单元测试题时间120分钟,满分150分。一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.某几何体的三视图,如图所示,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱[答案]B2.用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是()[答案]B[解析]D选项为主视图或侧视图,俯视图中显然应有一个被遮挡的圆,所以内圆是虚线,故选B.3.斜四棱柱的侧面是矩形的面最多有()A.0个B.1个C.2个D.3个[答案]C[解析]本题考查四棱柱的结构特征,画出示意图即可.4.已知△ABC是边长为2a的正三角形,那么△ABC的平面直观图△A′B′C′的面积为()A.a2B.a2C.a2D.a2[答案]C[解析]直观图面积S′与原图面积S具有关系:S′=S. S△ABC=(2a)2=a2,∴S△A′B′C′1=×a2=a2.5.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为()A.7B.6C.5D.3[答案]A[解析]设圆台较小底面圆的半径为r,由题意,另一底面圆的半径R=3r.∴S侧=π(r+R)l=π(r+3r)×3=84π,解得r=7.6.正方体内切球与外接球体积之比为()A.1B.13C.13D.19[答案]C[解析]设正方体棱长为a,内切球半径R1,外接球半径R2.R1=,R2=a,V内V外=()3(a)3=13.故选C.7.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是()A.30B.60C.30+135D.135[答案]A[解析]由菱形的对角线长分别是9和15,得菱形的边长为=,则这个菱柱的侧面积为4××5=30.8.半径为R的半圆卷成一个圆锥,则它的体积为()A.πR3B.πR3C.πR3D.πR3[答案]A[解析]依题意,得圆锥的底面周长为πR,母线长为R,则底面半径为,高为R,所以圆锥的体积为×π×()2×R=πR3.9.正三棱柱有一个半径为cm的内切球,则此棱柱的体积是()A.9cm3B.54cm3C.27cm3D.18cm3[答案]B[解析]由题意知棱柱的高为2cm,底面正三角形的内切圆的半径为cm,∴底面正三角形的边长为6cm,正三棱柱的底面面积为9cm2,∴此三棱柱的体积V=9×2=54(cm3).10.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.[答案]C2[解析]水平放置的正方体,当正视图为正方形时,其面积最小为1;当正视图为对角面时,其面积最大为.因此满足棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积的范围为[1,].由此可知,A,B,D均有可能,而<1,故C不可能.11.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,该四棱锥侧面积和体积分别是()A.4,8B.4,C.4(+1),D.8,8[答案]B[解析]因为四棱锥的侧棱长都相等,底面是正方形,所以该四棱锥为正四棱锥,其主视图为原图形中的△PEF,如图.由该四棱锥的主视图可知四棱锥的底面长AB=2,高PO=2,则四棱锥的斜高PE==.所以该四棱锥侧面积S=4××2×=4,体积=×2×2×2=.12.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为()A.cm3B.cm3C.cm3D.cm3[答案]A[解析]设球的半径为R,则由题知球被正方体上面截得圆的半径为4,球心到截面圆的距离为R-2,则R2=(R-2)2+42,解得R=5.∴球的体积为=cm3.二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.在几何体①圆锥;②正方体;③圆柱;④球;⑤正四面体中,三视图完全一样的是________.[答案]②④14.用斜二测画法画边长为2的正三角形的直观图时,如果在已知图形中取的x轴和正三角形的一边平行,则这个正三角形的直观图的面积是________.[答案]315.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为________.[答案]11[解析]设棱台的高为x,则有()2=,解之,得x=11.16.一个几何体的三视图及其尺寸如下图所示,其中主视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的...